88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/6
תוכן עניינים
קואורדינטות
משפט: יהא V מ"ו מעל שדה F, יהי 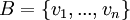 בסיס ל-V ויהי
בסיס ל-V ויהי 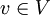 וקטור. אזי ל-v יש הצגה יחידה כצירוף לינארי לפי הבסיס B. כלומר, אם מתקיים
וקטור. אזי ל-v יש הצגה יחידה כצירוף לינארי לפי הבסיס B. כלומר, אם מתקיים 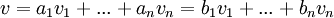 אזי בהכרח
אזי בהכרח 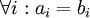 . (קל להוכיח את זה על ידי חיסור הצד הימני של המשוואה מהצד השמאלי, מקבלים צירוף לינארי שמתאפס עם מקדמים
. (קל להוכיח את זה על ידי חיסור הצד הימני של המשוואה מהצד השמאלי, מקבלים צירוף לינארי שמתאפס עם מקדמים 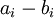 .)
.)
הגדרה: יהיו V,B וv כמו במשפט. אזי וקטור הקואורדינטות של v לפי בסיס B, מסומן ![[v]_B\in\mathbb{F}^n](/images/math/4/8/d/48d175f864d880e25a45feb85ad8c94e.png) מוגדר להיות
מוגדר להיות ![[v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}](/images/math/f/9/5/f95c4d5b167fb4c2880885415ca0e149.png) כאשר
כאשר 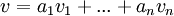 ההצגה הלינארית היחידה הקיימת לפי המשפט.
ההצגה הלינארית היחידה הקיימת לפי המשפט.
חשוב לזכור ![[v]_B=\begin{pmatrix}a_1 \\ a_2 \\ \vdots \\ a_n\end{pmatrix}](/images/math/f/9/5/f95c4d5b167fb4c2880885415ca0e149.png) אם"ם
אם"ם 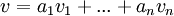
תרגיל קל אבל חשוב הוא להראות שלכל בסיס B מתקיים ש 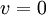 אם"ם
אם"ם ![[v]_B=0](/images/math/a/a/c/aac616b8c08680fd2fb1e1e5cccb8134.png) .
.
הערה: במרחבים הוקטוריים שאנו נעבוד איתם יש בסיסים סטנדרטיים. הייחוד של הבסיסים הסטנדרטיים הוא שקל מאד לחשב קואורדינטות לפיהם. נסתכל במרחבים וקטורים ובבסיסים הסטנדרטיים שלהם:
| מרחב וקטורי | בסיס סטנדרטי |
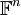
|
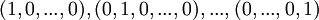
|
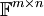
|

|
![\mathbb{F}_n[x]](/images/math/5/0/4/504c6115c35647a079e43b17f4468bef.png)
|
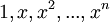
|
דוגמא.
חשב את הקואורדינטות של הוקטור 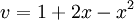 לפי הבסיס הסטנדרטי S של
לפי הבסיס הסטנדרטי S של ![\mathbb{R}_3[x]](/images/math/8/4/e/84ef8e18caf28275bb31fb78edc3a348.png) . למעשה הפולינום כמעט מוצג כצירוף לינארי של איברי הבסיס:
. למעשה הפולינום כמעט מוצג כצירוף לינארי של איברי הבסיס:
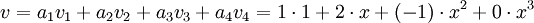 .
.
לפיכך ![[v]_S=(1,2,-1,0)](/images/math/7/2/c/72ce9c7c6545dbb68aececb179bddf8c.png) .
.
דוגמא.
חשב את הקואורדינטות של הוקטור 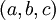 לפי הבסיס הסטנדרטי S של
לפי הבסיס הסטנדרטי S של 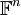 . קל לראות ש
. קל לראות ש ![[v]_S = (a,b,c)](/images/math/1/6/0/160aaa76dd5f1b407f9a424f38ca36ad.png) .
.
דוגמא.
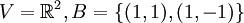 מצא את הקואורדינטות של הוקטור
מצא את הקואורדינטות של הוקטור 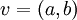 לפי הבסיס B. במקרה הכינותי מראש-
לפי הבסיס B. במקרה הכינותי מראש-
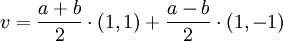
ולכן לפי ההגדרה ![[v]_B=(\frac{a+b}{2},\frac{a-b}{2})](/images/math/0/b/f/0bfb2b0112942154b05f33bb27cc4e3b.png)
אנו רואים שאין זה קל למצוא את הקואורדינטות לפי בסיס כלשהו שאינו הסטנדרטי.
תרגיל.
יהא V מ"ו ויהי B בסיס לו. יהיו 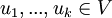 וקטורים כלשהם. הוכח:
וקטורים כלשהם. הוכח:
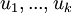 בת"ל אם"ם
בת"ל אם"ם ![[u_1]_B,...,[u_k]_B](/images/math/e/b/4/eb4b5b4e735834a276365d7282070e08.png) בת"ל
בת"ל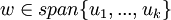 אם"ם
אם"ם ![[w]_B\in span\{[u_1]_B,...,[u_k]_B\}](/images/math/4/3/f/43f3b16647cd917a0ad42cf8adb05eb9.png)
נוכיח תרגיל זה בהמשך, לאחר שנלמד על העתקות לינאריות. כעת נניח שהוא נכון ונתרכז בכלי החישובי המשמעותי שקיבלנו; כל בדיקה/חישוב של תלות לינארית או פרישה בכל מרחב וקטורי (מטריצות, פולינומים, פונקציות) יכול בעצם להעשות במרחב הוקטורי המוכר והנוח 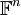 .
.
דוגמא.
האם הפולינומים 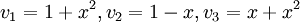 תלויים לינארית?
תלויים לינארית?
דבר ראשון, נעבור למרחב הקואורדינטות. מכיוון שבחירת הבסיס היא לשיקולנו, נבחר את הבסיס הסטנדרטי S של הפולינומים איתו קל לעבוד. מתקיים ש ![[v_1]_S=(1,0,1),[v_2]_S=(1,-1,0),[v_3]=(0,1,1)](/images/math/8/2/f/82f4358d3e0f0b5e6e7ea98bae8c8ff9.png)
הוכחנו בשיעור שעבר שוקטורים "רגילים" ת"ל אם"ם המטריצה שהם השורות שלה אינה הפיכה אם"ם הצורה המדורגת של המטריצה מכילה שורת אפסים. לכן, נשים את וקטורי הקואורדינטות בשורות מטריצה ונדרג.
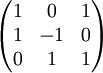
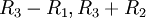
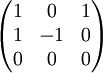
לכן וקטורי הקואורדינטות תלויים לינארית ולכן הפולינומים עצמם תלויים לינארית. נסכם את התהליך:
אלגוריתם לבדיקת תלות לינארית בין וקטורים
- הפוך את הוקטורים לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים
- שים את וקטורי הקואורדינטות בשורות מטריצה A
- הבא את המטריצה לצורה מדורגת
- אם באיזה שלב קיבלת שורת אפסים סימן שהוקטורים תלויים לינארית
- אם הגעת לצורה מדורגת ללא שורת אפסים סימן שהוקטורים בלתי תלויים לינארית
דוגמא.
האם המטריצה 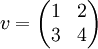 נפרשת על ידי המטריצות
נפרשת על ידי המטריצות
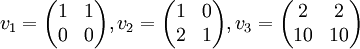 ? אם כן, הצג אותה כצירוף לינארי שלהן.
? אם כן, הצג אותה כצירוף לינארי שלהן.
פתרון: נעבור דבר ראשון למרחב הקואורדינטות לפי הבסיס הסטנדרטי 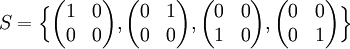
נקבל ![[v]_S=(1,2,3,4),[v_1]_S=(1,1,0,0),[v_2]_S=(1,0,2,1),[v_3]_S=(2,2,10,10)](/images/math/c/e/b/cebc685addea9d107edc1c2d44ec2667.png) .
.
למדנו בשיעור שעבר שוקטור b נפרש על ידי וקטורים מסויימים אם"ם קיים פתרון למערכת Ax=b כאשר A היא המטריצה שעמודותיה הם אותם וקטורים. הפתרון x הוא וקטורים הסקלרים מהצירוף הלינארי. לכן, אנו רוצים לדעת האם קיים פתרון למערכת ואם כן מהו:
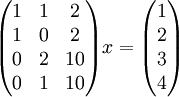
קל לפתור ולגלות ש 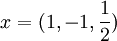 מקיים את המערכת ולכן מתקיים
מקיים את המערכת ולכן מתקיים 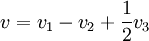
נסכם:
אלגוריתם לחישוב צירוף לינארי
- נתון וקטור b וקבוצת וקטורים. העבר את כולם לוקטורי קואורדינטות לפי הבסיס הסטנדרטי המתאים
- פתור את המערכת Ax=b כאשר עמודות A הינן וקטורי הקואורדינטות של קבוצת הוקטורים הפורשים
- אם אין פתרון, b לא נפרש על ידי האחרים
- אם קיים פתרון x אזי הוא מכיל את הסקלרים של הצירוף הלינארי בהתאם לסדר העמודות בA
מרחבי המטריצות
תהי מטריצה 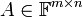 . מגדירים שלושה מרחבים עיקריים:
. מגדירים שלושה מרחבים עיקריים:
- מרחב השורות של A. זהו המרחב הנפרש על ידי שורות המטריצה A. נסמן
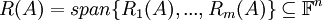
- מרחב העמודות של A. זהו המרחב הנפרש על ידי עמודות המטריצה A. נסמן
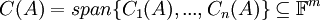
- מרחב השורות של A. זהו מרחב הפתרונות של המערכת ההומוגנית Ax=0. נסמן
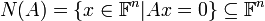
משפט: לכל מטריצה 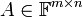 מתקיים
מתקיים 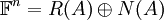
הגדרה: דרגת המטריצה A שווה למספר השורות בצורה המדורגת שלה השונות מאפס. מסומן rankA
משפט: 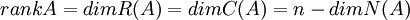 . אלה שווים למספר המשתנים התלויים, ומימד מרחב האפס שווה למספר המשתנים החופשיים.
. אלה שווים למספר המשתנים התלויים, ומימד מרחב האפס שווה למספר המשתנים החופשיים.
דוגמא.
מצא בסיס למרחב האפס של המטריצה 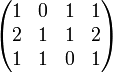
דבר ראשון, נדרג קנונית את המטריצה לקבל
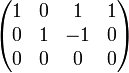
לפיכך המשתנה השלישי והרביעי הם חופשיים, נציב במקומם פרמטרים t,s והפתרון הכללי הוא מהצורה 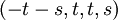 . תמיד ניתן לפרק את הפתרון הכללי לסכום של וקטורים קבועים כפול הסקלרים שהם הפרמטרים:
. תמיד ניתן לפרק את הפתרון הכללי לסכום של וקטורים קבועים כפול הסקלרים שהם הפרמטרים: 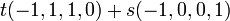 . וקטורים קבועים אלה תמיד מהווים בסיס למרחב הפתרונות:
. וקטורים קבועים אלה תמיד מהווים בסיס למרחב הפתרונות:
- אנו רואים שכל פתרון הוא צירוף לינארי של הוקטורים הללו עם הסקלרים שהם הפרמטרים (במקרה זה - t,s)
- וקטורים אלה תמיד בת"ל, שכן אם יש צירוף לינארי שלהם שמתאפס, מכיוון שהפרמטרים תמיד מופיעים לבדם בעמודה של המשתנה שלהם, הם חייבים להיות אפס
לכן הבסיס למרחב האפס הינו 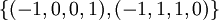
אלגוריתם למציאת בסיס למרחב האפס
- דרג את המטריצה קנונית
- הצב פרמטרים במקום המשתנים החופשיים
- מצא את הפתרון הכללי
- פרק את הפתרון הכללי לצירוף לינארי של וקטורים קבועים כפול הפרמטרים
- הוקטורים הקבועים מהווים בסיס למרחב האפס
תרגיל 7.31
נגדיר שני תתי מרחבים של ![\mathbb{R}_3[x]](/images/math/8/4/e/84ef8e18caf28275bb31fb78edc3a348.png) :
:
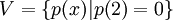 , ו
, ו 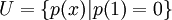
מצא את המימד של חיתוך המרחבים.
פתרון.
בתרגיל זה נשתמש בשיטה נפוצה ביותר. אנו מעוניינים לתאר את המרחבים הוקטוריים באופן קל יותר לעבודה מאשר התיאור לעיל; לכן ננסה לתאר את תתי המרחבים הללו כמרחבי אפס של מטריצות מתאימות. כמובן שכחלק מתהליך זה נעבור לוקטורי הקואורדינטות, הרי פולינום לא יכול להיות פתרון למערכת הומוגנית של מטריצות.
נביט בV. זהו אוסף כל הפולינומים ש2 הוא שורש שלהם. יהי פולינום כללי 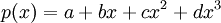 , הוא שייך לV אם"ם מקדמיו מקיימים את המשוואה הלינארית:
, הוא שייך לV אם"ם מקדמיו מקיימים את המשוואה הלינארית: 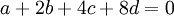 . באופן דומה הפולינום שייך לU אם"ם מקדמיו מקיימים את המשוואה הלינארית
. באופן דומה הפולינום שייך לU אם"ם מקדמיו מקיימים את המשוואה הלינארית 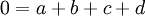 . לכן פולינום נמצא בחיתוך אם"ם מקדמיו (הקואורדינטות) מקיימים את מערכת המשוואות המכיל את שתי המשוואות הללו, כלומר מקדמיו הם מרחב האפס של המערכת.
. לכן פולינום נמצא בחיתוך אם"ם מקדמיו (הקואורדינטות) מקיימים את מערכת המשוואות המכיל את שתי המשוואות הללו, כלומר מקדמיו הם מרחב האפס של המערכת.
נמצא בסיס למרחב האפס 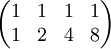 . נדרג קנונית לקבל
. נדרג קנונית לקבל
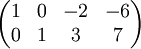
ולכן הפתרון הכללי הוא מהצורה 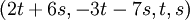 , ולכן בסיס למרחב האפס הינו
, ולכן בסיס למרחב האפס הינו 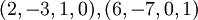 . נחזור מהקואורדינטות לצורה הפולינומית לקבל את התשובה הסופית:
. נחזור מהקואורדינטות לצורה הפולינומית לקבל את התשובה הסופית:
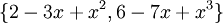 מהווים בסיס לחיתוך בין V לU.
מהווים בסיס לחיתוך בין V לU.
ראינו בהרצאה שפעולות שורה אינן משנות את המרחב הנפרש על ידי השורות. מכאן נובע האלגוריתם הבא:
אלגוריתם למציאת בסיס למרחב השורות (ומציאת בסיס לקבוצה כלשהי של וקטורים)
- שים את הקואורדינטות של הוקטורים לפי בסיס סטנדרטי מתאים בשורות מטריצה
- דרג את המטריצה
- השורות שאינן שורות אפסים בצורה המדורגת מהוות יחדיו בסיס למרחב השורות (או למרחב הקואורדינטות של הוקטורים שלנו)
מטריצות מעבר בין בסיסים
ראינו שקל מאד למצוא קואורדינטות לפי הבסיס הסטנדרטי, נשתמש בהנחה הזו בהמשך. אנו מעוניינים לדעת כיצד לחשב קואורדינטות לפי בסיס כלשהו, לאו דווקא סטנדרטי.
משפט: יהא V מ"ו ויהיו E,F בסיסים לו. אזי קיימת מטריצה יחידה המסומנת ![[I]^E_F](/images/math/2/b/d/2bdc7db12150a97716a9a1c21d1742c9.png) המקיימת את הפסוק הבא:
המקיימת את הפסוק הבא:
![\forall v\in V: [I]^E_F[v]_E=[v]_F](/images/math/1/7/b/17b12c597f8e46ebafb02da9deabffb8.png)
נסמן 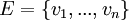 ו
ו 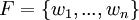 . אזי מתקיים ש
. אזי מתקיים ש![[I]^E_F](/images/math/2/b/d/2bdc7db12150a97716a9a1c21d1742c9.png) הינה המטריצה שעמודותיה הן
הינה המטריצה שעמודותיה הן ![[v_i]_F](/images/math/c/d/b/cdb0e6ced2f77815790fb78f605b8d84.png)
דוגמא.
הוכח ש ![[I]^S_B[I]^A_S=[I]^A_B](/images/math/6/5/3/653023384226547eafe4c3661a5e7113.png) . מכיוון שאנו יודעים שמטריצה המעבר הינה יחידה, מספיק להראות שהכפל מקיים את הפסוק מההגדרה:
. מכיוון שאנו יודעים שמטריצה המעבר הינה יחידה, מספיק להראות שהכפל מקיים את הפסוק מההגדרה:
![\forall v\in V: [I]^S_B[I]^A_S[v]_A=[I]^S_B[v]_S=[v]_B](/images/math/c/b/0/cb04c4351cb813abbb3f23bda4db1c4f.png)
משפט: לכל שני בסיסים E,F מטריצת המעבר הינה מטריצה הפיכה ומתקיים ![([I]^E_F)^{-1}=[I]^F_E](/images/math/b/3/f/b3f6080673f1a30c55100cc8718d3bcb.png)
מסקנה:
אלגוריתם למציאת מטריצת מעבר בין כל שני בסיסים E,F
- בחר בסיס סטנדרטי S מתאים למרחב שלך
- מצא את מטריצת המעבר
![[I]^E_S](/images/math/b/2/b/b2b4df7772480d67ed9e272792aad633.png) . זה קל מאד שכן יש למצוא את הקואורדינטות של איברי הבסיס E לפי הבסיס הסטנדרטי S
. זה קל מאד שכן יש למצוא את הקואורדינטות של איברי הבסיס E לפי הבסיס הסטנדרטי S - מצא את מטריצת המעבר
![[I]^F_S](/images/math/9/c/8/9c891851116631d866f8316d8559a34b.png) .
. - הפוך את המטריצה האחרונה לקבל
![([I]^F_S)^{-1}=[I]^S_F](/images/math/7/6/c/76cf328ff5b7b824008b828bf38d1f43.png)
- כפול את המטריצות על מנת לקבל את התוצאה הסופית
![[I]^S_F[I]^E_S=[I]^E_F](/images/math/a/a/7/aa79b74333d9c06ccafc41034ade00a7.png)