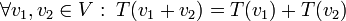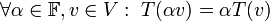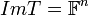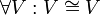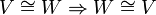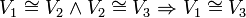הבדלים בין גרסאות בדף "88-112 לינארית 1 תיכוניסטים קיץ תשעא/מערך תרגול/8"
אחיה בר-און (שיחה | תרומות) (←משפט) |
אחיה בר-און (שיחה | תרומות) (←דוגמאות) |
||
| שורה 104: | שורה 104: | ||
T(a+bx+cx^{2})=aT(1)+bT(x)+cT(x^{2}) = \\ | T(a+bx+cx^{2})=aT(1)+bT(x)+cT(x^{2}) = \\ | ||
=a(x+2)+b(1)+c(-2x+1)=(2a+b+c)+(a-2c)x</math> | =a(x+2)+b(1)+c(-2x+1)=(2a+b+c)+(a-2c)x</math> | ||
| + | |||
| + | 2. | ||
| + | יהיו <math>\begin{pmatrix} 1\\ 2 \\ 3 \end{pmarix}</math> | ||
== הגדרות== | == הגדרות== | ||
גרסה מ־14:39, 21 ביולי 2015
תוכן עניינים
העתקות לינאריות (ה"ל)
הגדרה: יהיו 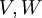 שני מ"ו מעל אותו שדה
שני מ"ו מעל אותו שדה 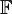 . ה"ל היא פונקציה
. ה"ל היא פונקציה 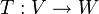 אם
אם
(או באופן שקול: אם לכל 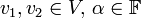 מתקיים
מתקיים 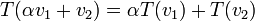 )
)
תכונות בסיסיות:
.1 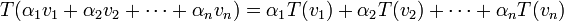
.2 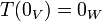
דוגמאות
1. יהיו  שניהם מעל
שניהם מעל 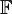 . תהא
. תהא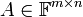 אזי העתקה
אזי העתקה 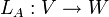 המוגדרת
המוגדרת  היא ה"ל.
היא ה"ל.
הוכחה: לכל 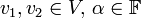 מתקיים
מתקיים
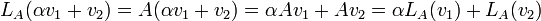
2. 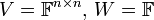 שניהם מעל
שניהם מעל 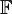 . אזי העתקה
. אזי העתקה 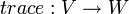 המגודרת
המגודרת 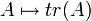 היא ה"ל.
היא ה"ל.
הוכחה: לכל 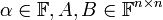

3. ![V=\mathbb{R}_{n}[x],\,W=\mathbb{R}_{n-1}[x]](/images/math/e/3/b/e3bb93e88ed069aa23de96c1fc0068e7.png) שניהם מעל
שניהם מעל 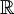 . אזי העתקה
. אזי העתקה 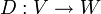 המגודרת
המגודרת 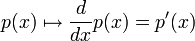 היא ה"ל.
היא ה"ל.
הוכחה:
![D[\alpha p_{1}(x)+p_{2}(x)]=[\alpha p_{1}(x)+p_{2}(x)]'=\alpha p_{1}'(x)+p_{2}'(x)=\alpha D[p_{1}(x)]+D[p_{2}(x)]](/images/math/2/1/2/212b3c164a73644cd93ef6149a1dd460.png)
4. העתקת הזהות 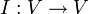 המוגדרת
המוגדרת 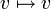 היא ה"ל.
היא ה"ל.
5. העתקת האפס 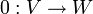 המוגדרת
המוגדרת 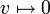 היא ה"ל.
היא ה"ל.
6. יהי 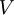 מ"ו מעל
מ"ו מעל 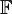 מימד
מימד 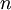 ויהי
ויהי 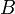 בסיס אזי הפונקציה
בסיס אזי הפונקציה 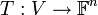 המוגדרת
המוגדרת ![v\mapsto [v]_B](/images/math/2/6/7/2670f477cf1b48d41e806ea128fae74d.png) היא ה"ל.
היא ה"ל.
דוגמאות נגדיות
1. יהיו 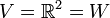 .
אזי העתקה
.
אזי העתקה 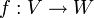 המוגדרת
המוגדרת
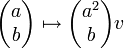 אינה ה"ל.
אינה ה"ל.
כי למשל
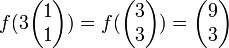
שלא שווה ל
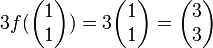
תרגיל
יהיו  שתי ה"ל.
שתי ה"ל. 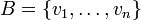 בסיס ל
בסיס ל 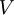 . נניח
. נניח 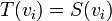 לכל
לכל 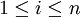
הוכח: 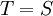 . כלומר לכל
. כלומר לכל 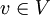 מתקיים
מתקיים 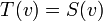
הוכחה: יהי 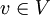 אזי
אזי 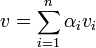 כי
כי 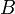 בסיס ובפרט פורשת.
ואז
בסיס ובפרט פורשת.
ואז
עיבוד הנוסחה נכשל (שגיאת תחביר): T(v)=T(\alpha_{1}v_{1}+\alpha_{2}v_{2}+\cdots+\alpha_{n}v_{n})=\alpha_{1}T(v_{1})+\alpha_{2}T(v_{2})+\cdots+\alpha_{n}T(v_{n}) = \\ = \alpha_{1}S(v_{1})+\alpha_{2}S(v_{2})+\cdots+\alpha_{n}S(v_{n})=S(\alpha_{1}v_{1}+\alpha_{2}v_{2}+\cdots+\alpha_{n}v_{n})=S(v)
משפט ההגדרה
יהיו 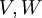 שני מ"ו מעל
שני מ"ו מעל 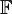 . יהי
. יהי 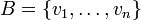 בסיס ל
בסיס ל 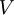 ויהיו
ויהיו 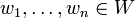 וקטורים כלשהם.
וקטורים כלשהם.
אזי קימת ה"ל יחידה 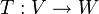 כך ש
כך ש 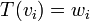 לכל
לכל 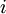
מסקנה ניתן להגדיר ה"ל יחידה ע"י קביעה לאן ישלח בסיס ל V
דוגמאות
1.
![V=\mathbb{R}_{2}[x]](/images/math/f/7/3/f73cc35842c78e71bd2b26bb136b5c6a.png) מצא את הה"ל
מצא את הה"ל 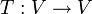 המקימת
המקימת 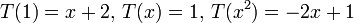 . כתוב את העתקה מפורשות, כלומר לאן
. כתוב את העתקה מפורשות, כלומר לאן 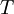 שולחת פולינום כללי
שולחת פולינום כללי 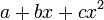
פתרון: עיבוד הנוסחה נכשל (שגיאת תחביר): T(a+bx+cx^{2})=aT(1)+bT(x)+cT(x^{2}) = \\ =a(x+2)+b(1)+c(-2x+1)=(2a+b+c)+(a-2c)x
2.
יהיו עיבוד הנוסחה נכשל (פונקציה \end לא מוכרת): \begin{pmatrix} 1\\ 2 \\ 3 \end{pmarix}
הגדרות
תהא 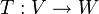 ה"ל.
ה"ל.
- הגרעין של
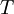 מוגדר
מוגדר 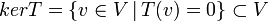
- התמונה של
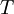 מוגדרת
מוגדרת 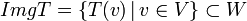
- הדרגה של
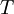 מוגדרת
מוגדרת 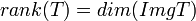
דוגמאות
1.
יהיו 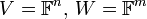 . תהא
. תהא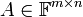 ונסתכל על העתקה
ונסתכל על העתקה 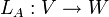 המוגדרת
המוגדרת  .
אזי
.
אזי
2.
יהי 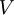 מ"ו מעל
מ"ו מעל 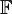 מימד
מימד 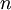 ויהי
ויהי 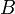 בסיס והעל הלינארית
בסיס והעל הלינארית 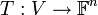 המוגדרת
המוגדרת ![v\mapsto [v]_B](/images/math/2/6/7/2670f477cf1b48d41e806ea128fae74d.png) .
.
אזי
משפט
תהא 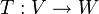 ה"ל.
ה"ל.
אזי 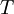 חח"ע
חח"ע 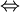 מתקיים כי
מתקיים כי 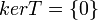
תרגיל:
תהא 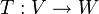 ה"ל. ויהיו
ה"ל. ויהיו 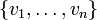 וקטורים ב
וקטורים ב 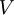 אזי
אזי
- אם
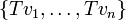 בת"ל אז
בת"ל אז 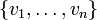 בת"ל
בת"ל - אם
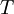 חח"ע אז גם הכיוון ההפוך נכון. כלומר אם
חח"ע אז גם הכיוון ההפוך נכון. כלומר אם 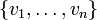 בת"ל אז
בת"ל אז 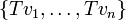
הוכחה
- נניח
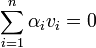 . נפעיל
. נפעיל 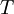 על שני האגפים ונקבל מלינאריות של
על שני האגפים ונקבל מלינאריות של 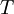 כי
כי 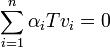 . כיוון שנתון ש
. כיוון שנתון ש 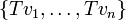 בת"ל נקבל כי
בת"ל נקבל כי 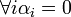 כנדרש.
כנדרש. - נניח כי
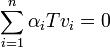 . מלינאריות נקבל כי
. מלינאריות נקבל כי 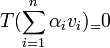 כיוון ש
כיוון ש 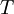 חח"ע נקבל כי
חח"ע נקבל כי 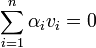 . כיוון ש
. כיוון ש 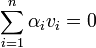 בת"ל נקבל כי
בת"ל נקבל כי 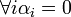 כנדרש.
כנדרש.
תרגיל
![V=\mathbb{R}_{2}[x],\,W=\mathbb{R}^{2}](/images/math/2/c/1/2c10a1615373fc1ae565132222c34e7d.png) האם קימת
האם קימת 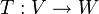 ה"ל חח"ע?
ה"ל חח"ע?
פתרון: נניח בשלילה כי 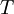 חח"ע אזי כיוון ש
חח"ע אזי כיוון ש 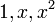 בתל גם
בתל גם 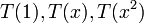 בת"ל אבל
בת"ל אבל 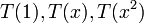 שייכים למרחב וקטורי מימד 2 ולכן הקבוצה הבת"ל המקס' היא מגודל 2.
שייכים למרחב וקטורי מימד 2 ולכן הקבוצה הבת"ל המקס' היא מגודל 2.
תרגיל
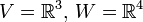 האם קימת
האם קימת 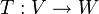 ה"ל על?
ה"ל על?
פתרון: נניח בשלילה כי 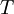 על אזי יש מקור ל
על אזי יש מקור ל 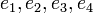 . נסמן את המקורות ב
. נסמן את המקורות ב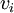 כלומר
כלומר 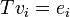 . כיוון ש
. כיוון ש 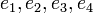 בת"ל גם
בת"ל גם 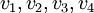 בת"ל אבל
בת"ל אבל 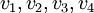 שייכים למרחב וקטורי מימד 3 ולכן הקבוצה הבת"ל המקס' היא מגודל 3.
שייכים למרחב וקטורי מימד 3 ולכן הקבוצה הבת"ל המקס' היא מגודל 3.
תרגיל
תהא 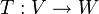 ה"ל. תהא
ה"ל. תהא 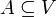 תת קבוצה. אזי
תת קבוצה. אזי 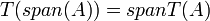
הוכחה:
(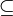 ) יהא
) יהא 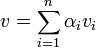 צ"ל באיברי
צ"ל באיברי 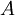 אזי
אזי 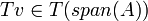 הוא איבר כללי.
הוא איבר כללי.
כעת 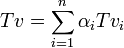 שזה צ"ל באיברי
שזה צ"ל באיברי 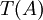 ולכן שייך ל
ולכן שייך ל 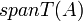
(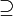 ) יהא צ"ל באיברי
) יהא צ"ל באיברי 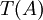 אזי הוא מהצורה
אזי הוא מהצורה 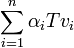 כאשר
כאשר 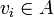
מלינאריות נקבל כי 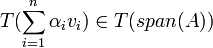
מסקנה לכל תת מרחב 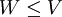 מתקיים כי
מתקיים כי 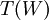 תת מרחב.
תת מרחב.
תרגיל
יהיו 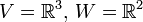 והמישור
והמישור
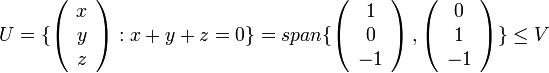
מצא ה"ל 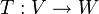 כך ש
כך ש 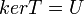 וגם
וגם
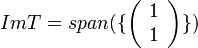
פתרון
נשלים לבסיס ל V
בעזרת
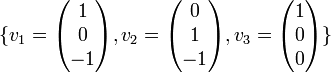
לפי משפט ההגדרה מספיק להגדיר 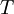 בעזרת הבסיס.
בעזרת הבסיס.
נגדיר 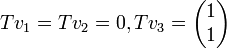
ואז
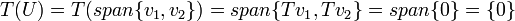 ולכן
ולכן 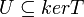
בכיוון השני, יהיה 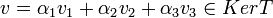 אזי
אזי 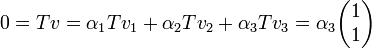 ולכן
ולכן 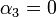 ואז
ואז 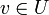
בנוסף, באופן דומה,
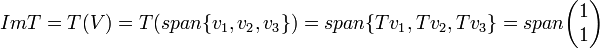
כנדרש.
תרגיל
תהא 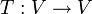 ה"ל,
ה"ל, 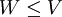 ת"מ. נתון כי
ת"מ. נתון כי 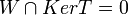 . הוכח כי
. הוכח כי 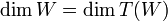
הוכחה:
נסתכל על ה"ל 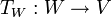 אזי מתקיים כי
אזי מתקיים כי 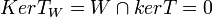 ולכן
ולכן 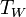 חח"ע. אם נבחר בסיס ל
חח"ע. אם נבחר בסיס ל 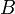 אזי
אזי 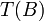 גם כן בסיס
גם כן בסיס
ואז 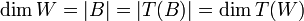
משפט הדרגה
תהא 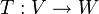 ה"ל. אזי
ה"ל. אזי 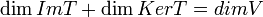
הערה: שימו לב שזה הכללה עבור מטריצה 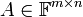 ומשפט
ומשפט 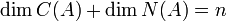 (זיכרו שמטריצה היא מקרה פרטי של ה"ל)
(זיכרו שמטריצה היא מקרה פרטי של ה"ל)
תרגיל
נסתכל על ה"ל 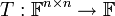 המוגדרת
המוגדרת 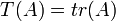 מצt בסיס לגרעין העתקה.
מצt בסיס לגרעין העתקה.
פתרון:
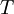 היא על כי לכל
היא על כי לכל 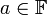 יש מקור. למשל
יש מקור. למשל 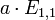 .
לכן
.
לכן 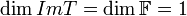 ממשפט הדרגה נסיק כי
ממשפט הדרגה נסיק כי 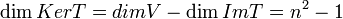
כעת לפי משפט השלישי חינם מספיק למצוא 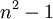 מטריצות בת"ל ששיכות לגרעין ואז הם יהיו בסיס.
מטריצות בת"ל ששיכות לגרעין ואז הם יהיו בסיס.
למשל המטריצות 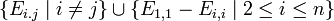
בקבוצה זאת יש אכן 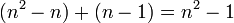 מטריצות בת"ל
מטריצות בת"ל
הפיכות ואיזמורפיזם
ה"ל 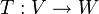 היא הפיכה אם יש ה"ל
היא הפיכה אם יש ה"ל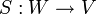 כך ש:
כך ש: 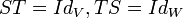 . במקרה זה מסמנים
. במקרה זה מסמנים 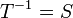
משפט
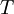 הפיכה אמ"מ
הפיכה אמ"מ 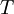 חח"ע ועל
חח"ע ועל
(שימו לב שידוע שפונקציה חח"ע ועל היא הפיכה כפונקציה. המשפט אומר שבמקרה זה הפונקציה היא ה"ל)
תכונות
- אם
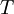 הפיכה אז גם ההופכית ומתקיים
הפיכה אז גם ההופכית ומתקיים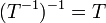
-
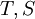 הפיכות אמ"מ ההרכבה
הפיכות אמ"מ ההרכבה 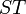 הפיכה. במקרה זה מתקיים
הפיכה. במקרה זה מתקיים 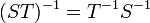
- אם ה"ל
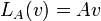 הפיכה אז ההופכית היא
הפיכה אז ההופכית היא 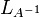
איזומורפיזם
הגדרה ה"ל 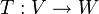 תקרא
תקרא
- מונומורפיזם אם
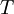 חח"ע
חח"ע - אפימורפיזם אם
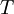 על
על - איזומורפיזם אם
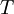 חח"ע ועל (כלומר הפיכה). במקרה זה נאמר ש
חח"ע ועל (כלומר הפיכה). במקרה זה נאמר ש 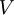 ו
ו 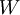 איזומורפים ונסמן
איזומורפים ונסמן 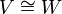
הערה: 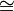 מתנהג כמו יחס שקילות. כלומר
מתנהג כמו יחס שקילות. כלומר
הערה 2 מרחבים איזומורפים בעצם אומר שהם "אותו דבר" במובן מסוים. יש להם אותו מבנה במובן שאם "נטשטש" את זהות האיברים ונסתכל רק על המבנה (למשל שחיבור של שני וקטורים מסוימים שווה וקטור מסוים אחר) אז נראה אותו דבר בשני המרחבים.
דוגמא: 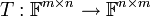 המוגדרת
המוגדרת 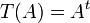 היא איזומורפיזם.
היא איזומורפיזם.
משפט
יהיו 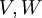 שני מרחבים וקטורים. אזי
שני מרחבים וקטורים. אזי
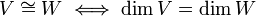
"הוכחה"
(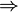 ) נבחר בסיס
) נבחר בסיס 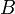 עבור
עבור 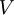 . מהנתון, קיימת
. מהנתון, קיימת 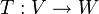 הפיכה. לכן
הפיכה. לכן 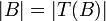 ובנוסף,
ובנוסף, 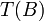 בסיס ל
בסיס ל 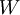 . זה אומר שהמימדים שווים.
. זה אומר שהמימדים שווים.
(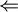 ) נבחר
) נבחר 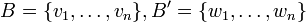 בסיסים. לפי משפט ההגדרה נגדיר
בסיסים. לפי משפט ההגדרה נגדיר 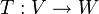 ע"י
ע"י 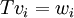 . במקרה זה
. במקרה זה 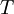 ה"ל הפיכה, כלומר המרחבים איזומורפים.
ה"ל הפיכה, כלומר המרחבים איזומורפים.
הערה אפשר למצוא את איזו' בצורה מפורשת ע"י הצגה לפי בסיס
אם נגדיר 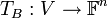 המוגדרת ע"י
המוגדרת ע"י ![T(v)=[v]_B](/images/math/7/d/7/7d7222461f1e6cf076fb03347925a9ae.png) כאשר
כאשר 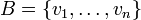 היא איזומורפיזם.
היא איזומורפיזם.
כעת עבור מציאת איזו' בין 2 מרחבים 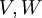 זה פשוט יהיה
זה פשוט יהיה 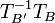 כאשר
כאשר 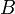 בסיס ל
בסיס ל 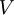 ו-
ו- 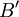 בסיס ל
בסיס ל 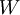
דוגמא
![\mathbb{C}^{2\times 3} \cong \mathbb{C}^6 \cong \mathbb{C}_5 [x] \cong span\{e_1, e_7, e_{12},e_{101}\}](/images/math/5/a/5/5a541021aafbc21e1eeb18c60e151ac7.png)