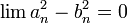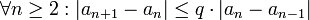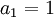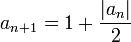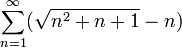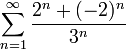הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעה/בוחן 1 - פתרון"
איתמר שטיין (שיחה | תרומות) (←שאלה 2 (40 נק)) |
איתמר שטיין (שיחה | תרומות) (←שאלה 1 (30 נק)) |
||
| (12 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 9: | שורה 9: | ||
'''הוכיחו/הפריכו:''' | '''הוכיחו/הפריכו:''' | ||
::<math>\lim a_n^2-b_n^2= 0</math> | ::<math>\lim a_n^2-b_n^2= 0</math> | ||
| + | |||
| + | פתרון משופר ומעודכן: הטענה נכונה. | ||
| + | נשים לב ש | ||
| + | |||
| + | <math>(a_n)^2-(b_n)^2=(a_n+b_n)(a_n-b_n)</math> | ||
| + | |||
| + | עכשיו, ידוע כי <math>\displaystyle{\lim_{n\to \infty}} a_n-b_n=0</math> | ||
| + | |||
| + | לכן אם נוכיח כי <math>a_n+b_n</math> היא סדרה חסומה, נקבל כי אכן <math>\displaystyle{\lim_{n\to\infty}} a_n^2-b_n^2= 0</math>. | ||
| + | |||
| + | לכן נותר להוכיח כי <math>a_n+b_n</math> סדרה חסומה. | ||
| + | |||
| + | היות ש <math>\displaystyle{\lim_{n\to \infty}} (a_{n})^2+(b_{n})^2=L\in\mathbb{R}</math> | ||
| + | |||
| + | נקבל כי הסדרה <math>(a_{n})^2+(b_{n})^2</math> חסומה. | ||
| + | |||
| + | אבל <math>0\leq(a_{n})^2\leq(a_{n})^2+(b_{n})^2</math> | ||
| + | |||
| + | ולכן גם <math>(a_{n})^2</math> סדרה חסומה ולכן גם <math>a_n</math> חסומה. | ||
| + | |||
| + | באופן דומה מראים ש <math>b_n</math> חסומה ולכן גם סכומן חסום כנדרש. | ||
| + | |||
===סעיף ב=== | ===סעיף ב=== | ||
| שורה 17: | שורה 39: | ||
(רמז: יש בשאלה הזו '''קושי''') | (רמז: יש בשאלה הזו '''קושי''') | ||
| + | |||
| + | פתרון: יש פתרון כאן | ||
| + | |||
| + | [[88-132 אינפי 1 סמסטר א' תשעב/מערך תרגול/סדרות/קושי|מערך תרגול על סדרות קושי]] | ||
==שאלה 2 (40 נק)== | ==שאלה 2 (40 נק)== | ||
| שורה 37: | שורה 63: | ||
בלי הגבלת כלליות נניח ש <math>\sup(B)\leq\sup(A)</math> ולכן <math>\max\{\sup(A),\sup(B)\}=\sup(A)</math> | בלי הגבלת כלליות נניח ש <math>\sup(B)\leq\sup(A)</math> ולכן <math>\max\{\sup(A),\sup(B)\}=\sup(A)</math> | ||
| − | נסמן <math>\sup(A)= | + | נסמן <math>\sup(A)=s</math>. |
| − | נוכיח ש <math> | + | נוכיח ש <math>s</math> מקיים את שתי התכונות של<math>\sup(A\cup B)</math> |
| − | א) חסם מלעיל: יהי <math>x\in A\cup B</math>. אם <math>x\in A</math> אז בוודאי | + | תכונה א) חסם מלעיל: יהי <math>x\in A\cup B</math>. אם <math>x\in A</math> אז בוודאי |
| − | <math>x\leq \sup(A) = | + | <math>x\leq \sup(A) = s</math> |
ואם <math>x\in B</math> אז | ואם <math>x\in B</math> אז | ||
| − | <math>x\leq \sup(B) \leq \sup(A)= | + | <math>x\leq \sup(B) \leq \sup(A)=s</math> |
| − | ולכן <math> | + | ולכן <math>s</math> אכן חסם מלעיל של <math>A\cup B</math> |
| + | |||
| + | תכונה ב) חסם מלעיל הכי קטן: נניח ש <math>m<s</math> (צריך להראות ש <math>m</math> אינו חסם מעליל של <math>A\cup B</math>) | ||
| + | |||
| + | היות ש <math>m<s=\sup(A)</math> אז קיים <math>a\in A</math> כך ש <math>m<a</math> (לפי תכונה של חסם עליון של <math>A</math>) | ||
| + | |||
| + | אבל בוודאי <math>a\in A\cup B</math> כלומר קיים איבר <math>a\in A\cup B</math> כך ש <math>m<a</math> ולכן <math>m</math> אינו חסם מלעיל של <math>A\cup B</math> כנדרש. | ||
| + | |||
| + | אכן הוכחנו כי <math>s</math> חסם עליון של <math>A\cup B</math>. ובזה סיימנו. | ||
===סעיף ב=== | ===סעיף ב=== | ||
| שורה 96: | שורה 130: | ||
הוכיחו כי הסדרה מתכנסת ומצאו את גבולה | הוכיחו כי הסדרה מתכנסת ומצאו את גבולה | ||
| + | |||
| + | פתרון: | ||
| + | |||
| + | נרצה להוכיח כי הסדרה מונוטונית עולה וחסומה. | ||
| + | |||
| + | ראשית נשים לב שהסדרה חיובית כי תמיד <math>a_n=1+\frac{|a_n|}{2}>0</math>. (וגם <math>a_1=1>0</math>) | ||
| + | |||
| + | לכן אפשר לכתוב את הסדרה | ||
| + | |||
| + | <math>a_{n+1}=1+\frac{a_n}{2}</math> | ||
| + | |||
| + | כעת נוכיח באינדוקציה שהיא מונוטונית עולה: | ||
| + | |||
| + | 1) מונוטונית עולה: צריך להראות ש <math>a_{n+1}\geq a_n</math> | ||
| + | |||
| + | עבור: <math>n=1</math> זה אכן נכון כי | ||
| + | |||
| + | <math>a_2=1+\frac{1}{2}=\frac{3}{2}>1=a_1</math> | ||
| + | |||
| + | נניח שהטענה הכונה עבור <math>n</math> כלומר: <math>a_{n+1}\geq a_n</math> | ||
| + | |||
| + | נוכיח עבור <math>n+1</math> כלומר נוכיח כי | ||
| + | |||
| + | <math>a_{n+2}\geq a_{n+1}</math> | ||
| + | |||
| + | זה נכון מפני ש | ||
| + | |||
| + | <math>a_{n+2}=1+\frac{a_{n+1}}{2}\geq 1+\frac{a_n}{2}=a_{n+1}</math> | ||
| + | |||
| + | ובזאת הוכחנו שהיא מונוטונית עולה. | ||
| + | |||
| + | נוכיח שהסדרה חסומה מלעיל ע"י 2, באינדוקציה: | ||
| + | |||
| + | 2) חסימות מלעיל: צריך להראות ש <math>a_n\leq 2</math>. | ||
| + | |||
| + | עבור <math>n=1</math> אכן <math>a_1=1<2</math>. | ||
| + | |||
| + | נניח שעבור <math>n</math> מתקיים <math>a_n\leq 2</math>. | ||
| + | |||
| + | אז גם עבור <math>n+1</math> מתקיים | ||
| + | |||
| + | <math>a_{n+1}=1+\frac{a_n}{2}\leq 1+\frac{2}{2}=2</math> | ||
| + | |||
| + | כנדרש. | ||
| + | |||
| + | לכן זו סדרה מונוטונית עולה וחסומה מלעיל ולכן היא מתכנסת. נסמן את גבולה ב <math>L</math>. | ||
| + | |||
| + | נמצא את הגבול באמצעות הטריק הרגיל. | ||
| + | |||
| + | נפעיל <math>\displaystyle{\lim_{n\to\infty}}</math> בשני אגפים של המשוואה | ||
| + | |||
| + | <math>a_{n+1}=1+\frac{a_n}{2}</math> | ||
| + | |||
| + | ונקבל | ||
| + | |||
| + | <math>L=1+\frac{L}{2}</math> | ||
| + | |||
| + | כלומר | ||
| + | |||
| + | <math>L=2</math>. | ||
| + | |||
| + | ובזה סיימנו את הפתרון. | ||
===סעיף ב=== | ===סעיף ב=== | ||
קבעו אם הטורים הבאים מתכנסים | קבעו אם הטורים הבאים מתכנסים | ||
| + | 1) | ||
::<math>\sum_{n=1}^\infty (\sqrt{n^2+n+1}-n)</math> | ::<math>\sum_{n=1}^\infty (\sqrt{n^2+n+1}-n)</math> | ||
| + | פתרון: נשים לב ש | ||
| + | |||
| + | <math>\displaystyle{\lim_{n\to\infty}}\sqrt{n^2+n+1}-n=\displaystyle{\lim_{n\to\infty}}\frac{(\sqrt{n^2+n+1}-n)(\sqrt{n^2+n+1}+n)}{\sqrt{n^2+n+1}+n}=\displaystyle{\lim_{n\to\infty}}\frac{n^2+n+1-n^2}{\sqrt{n^2+n+1}+n}</math> | ||
| + | |||
| + | <math>=\displaystyle{\lim_{n\to\infty}}\frac{1+\frac{1}{n}}{\sqrt{1+\frac{1}{n}+\frac{1}{n^2}}+1}=\frac{1}{2}</math> | ||
| + | |||
| + | כלומר הסדרה בתוך הטור לא מתכנסת ל 0 ולכן הטור מתבדר. | ||
| + | |||
| + | 2) | ||
::<math>\sum_{n=1}^\infty\frac{2^n+(-2)^n}{3^n}</math> | ::<math>\sum_{n=1}^\infty\frac{2^n+(-2)^n}{3^n}</math> | ||
| + | |||
| + | פתרון: נשים לב שזה בעצם סכום של שני הטורים | ||
| + | |||
| + | <math>\sum_{n=1}^\infty\frac{2^n}{3^n}+\sum_{n=1}^\infty\frac{(-2)^n}{3^n}=\sum_{n=1}^\infty(\frac{2}{3})^n+\sum_{n=1}^\infty(\frac{-2}{3})^n</math> | ||
| + | |||
| + | כל אחד מהטורים האלה הוא טור הנדסי שהמנה שלו בין <math>-1</math> ל <math>1</math> ולכן הוא טור מתכנס. | ||
| + | |||
| + | ולכן גם סכומם שהוא הטור שלנו, מתכנס. | ||
גרסה אחרונה מ־21:05, 28 בדצמבר 2014
תוכן עניינים
שאלה 1 (30 נק)
סעיף א
תהיינה שתי סדרות 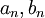 כך ש:
כך ש:
- 1.
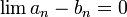
- 2.
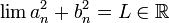
- 1.
הוכיחו/הפריכו:
פתרון משופר ומעודכן: הטענה נכונה. נשים לב ש
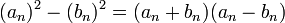
עכשיו, ידוע כי 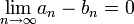
לכן אם נוכיח כי 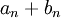 היא סדרה חסומה, נקבל כי אכן
היא סדרה חסומה, נקבל כי אכן 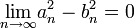 .
.
לכן נותר להוכיח כי 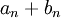 סדרה חסומה.
סדרה חסומה.
היות ש 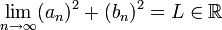
נקבל כי הסדרה 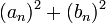 חסומה.
חסומה.
אבל 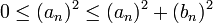
ולכן גם 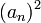 סדרה חסומה ולכן גם
סדרה חסומה ולכן גם 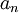 חסומה.
חסומה.
באופן דומה מראים ש 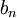 חסומה ולכן גם סכומן חסום כנדרש.
חסומה ולכן גם סכומן חסום כנדרש.
סעיף ב
תהי סדרה 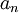 וקבוע
וקבוע 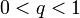 כך ש
כך ש
הוכיחו כי 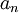 מתכנסת.
מתכנסת.
(רמז: יש בשאלה הזו קושי)
פתרון: יש פתרון כאן
שאלה 2 (40 נק)
סעיף א
לכל שתי קבוצות לא ריקות וחסומות מלעיל.
- 1. הוכיחו/הפריכו:
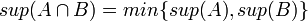
- 2. הוכיחו/הפריכו:
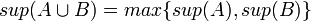
- 1. הוכיחו/הפריכו:
פתרון:
1) לא נכון. ניקח 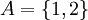 ו
ו 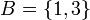
אז 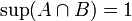
אבל 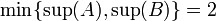
2) נכון.
בלי הגבלת כלליות נניח ש 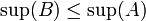 ולכן
ולכן 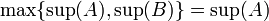
נסמן 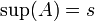 .
.
נוכיח ש 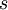 מקיים את שתי התכונות של
מקיים את שתי התכונות של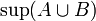
תכונה א) חסם מלעיל: יהי 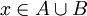 . אם
. אם 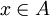 אז בוודאי
אז בוודאי
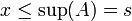
ואם 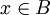 אז
אז
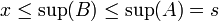
ולכן 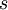 אכן חסם מלעיל של
אכן חסם מלעיל של 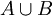
תכונה ב) חסם מלעיל הכי קטן: נניח ש 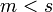 (צריך להראות ש
(צריך להראות ש 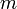 אינו חסם מעליל של
אינו חסם מעליל של 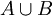 )
)
היות ש 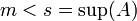 אז קיים
אז קיים 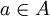 כך ש
כך ש 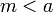 (לפי תכונה של חסם עליון של
(לפי תכונה של חסם עליון של 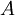 )
)
אבל בוודאי 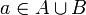 כלומר קיים איבר
כלומר קיים איבר 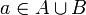 כך ש
כך ש 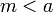 ולכן
ולכן 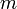 אינו חסם מלעיל של
אינו חסם מלעיל של 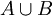 כנדרש.
כנדרש.
אכן הוכחנו כי 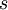 חסם עליון של
חסם עליון של 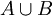 . ובזה סיימנו.
. ובזה סיימנו.
סעיף ב
נניח 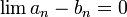 .
.
- הוכיחו/הפריכו:
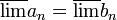
- הוכיחו/הפריכו:
פתרון: הטענה נכונה.
תהי 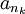 תת סדרה של
תת סדרה של 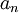 כך ש
כך ש
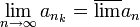
(הרי יש תת סדרה שמתכנסת לגבול העליון)
היות ש 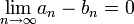 ,
,
אז כמובן ש
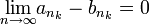
(כי תת סדרה של סדרה מתכנסת, מתכנסת לאותו מספר).
ולכן
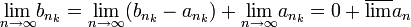
כלומר 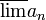 הוא גם גבול חלקי של
הוא גם גבול חלקי של 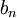 ולכן
ולכן
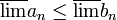 (כי
(כי 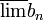 הוא הגבול החלקי הגדול ביותר)
הוא הגבול החלקי הגדול ביותר)
בדרך דומה מוכיחים
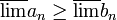
ולכן
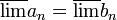
כנדרש
שאלה 3 (30 נק)
סעיף א
תהי סדרה המוגדרת ע"י כלל הנסיגה
הוכיחו כי הסדרה מתכנסת ומצאו את גבולה
פתרון:
נרצה להוכיח כי הסדרה מונוטונית עולה וחסומה.
ראשית נשים לב שהסדרה חיובית כי תמיד 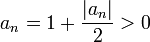 . (וגם
. (וגם 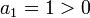 )
)
לכן אפשר לכתוב את הסדרה
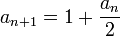
כעת נוכיח באינדוקציה שהיא מונוטונית עולה:
1) מונוטונית עולה: צריך להראות ש 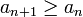
עבור: 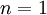 זה אכן נכון כי
זה אכן נכון כי
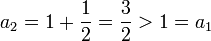
נניח שהטענה הכונה עבור 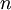 כלומר:
כלומר: 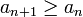
נוכיח עבור 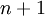 כלומר נוכיח כי
כלומר נוכיח כי
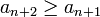
זה נכון מפני ש
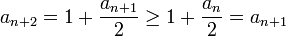
ובזאת הוכחנו שהיא מונוטונית עולה.
נוכיח שהסדרה חסומה מלעיל ע"י 2, באינדוקציה:
2) חסימות מלעיל: צריך להראות ש 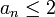 .
.
עבור 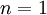 אכן
אכן 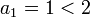 .
.
נניח שעבור 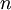 מתקיים
מתקיים 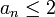 .
.
אז גם עבור 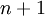 מתקיים
מתקיים
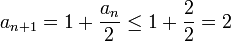
כנדרש.
לכן זו סדרה מונוטונית עולה וחסומה מלעיל ולכן היא מתכנסת. נסמן את גבולה ב 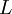 .
.
נמצא את הגבול באמצעות הטריק הרגיל.
נפעיל 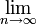 בשני אגפים של המשוואה
בשני אגפים של המשוואה
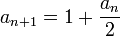
ונקבל
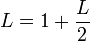
כלומר
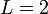 .
.
ובזה סיימנו את הפתרון.
סעיף ב
קבעו אם הטורים הבאים מתכנסים
1)
פתרון: נשים לב ש
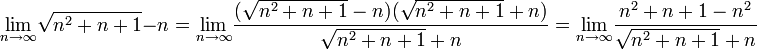
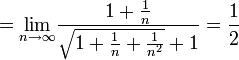
כלומר הסדרה בתוך הטור לא מתכנסת ל 0 ולכן הטור מתבדר.
2)
פתרון: נשים לב שזה בעצם סכום של שני הטורים
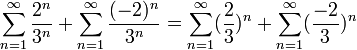
כל אחד מהטורים האלה הוא טור הנדסי שהמנה שלו בין 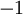 ל
ל 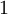 ולכן הוא טור מתכנס.
ולכן הוא טור מתכנס.
ולכן גם סכומם שהוא הטור שלנו, מתכנס.