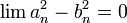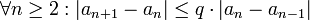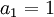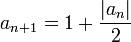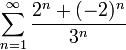הבדלים בין גרסאות בדף "88-132 אינפי 1 סמסטר א' תשעה/בוחן 1 - פתרון"
איתמר שטיין (שיחה | תרומות) (←סעיף א) |
איתמר שטיין (שיחה | תרומות) (←סעיף א) |
||
| שורה 104: | שורה 104: | ||
הוכיחו כי הסדרה מתכנסת ומצאו את גבולה | הוכיחו כי הסדרה מתכנסת ומצאו את גבולה | ||
| + | |||
| + | (בכתיבה) | ||
| + | |||
| + | נרצה להוכיח כי הסדרה מונוטונית עולה וחסומה. | ||
| + | |||
| + | ראשית נוכיח שהסדרה חיובית (מה שדי ברור). למען הדיוק נוכיחזאת באופן מסודר באינדוקציה. | ||
| + | |||
| + | כלומר רוצים להוכיח ש <math>a_n\geq 0</math>. | ||
| + | |||
| + | עבור <math>n=1</math> אכן <math>a_1>=1\geq 0</math>. | ||
| + | |||
| + | |||
| + | |||
| + | 1) מונוטונית עולה: צריך להראות ש <math>a_{n+1}\geqa_n</math> | ||
| + | |||
| + | עבור: <math>n=1</math> זה אכן נכון כי | ||
| + | |||
| + | <math>a_2=1+\frac{1}{2}=\frac{3}{2}>1=a_1</math> | ||
| + | |||
| + | נניח שהטענה הכונה עבור <math>n</math> כלומר: <math>a_{n+1}\geqa_n</math> | ||
| + | |||
| + | נוכיח עבור <math>n+1</math> כלומר נוכיח כי | ||
| + | |||
| + | <math>a_{n+2}\geq a_{n+1}</math> | ||
| + | |||
| + | זה נכון מפני ש | ||
| + | |||
| + | <math>a_{n+2}=\frac</math> | ||
===סעיף ב=== | ===סעיף ב=== | ||
גרסה מ־09:00, 24 בדצמבר 2014
תוכן עניינים
שאלה 1 (30 נק)
סעיף א
תהיינה שתי סדרות 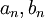 כך ש:
כך ש:
- 1.
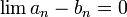
- 2.
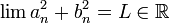
- 1.
הוכיחו/הפריכו:
סעיף ב
תהי סדרה 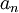 וקבוע
וקבוע 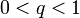 כך ש
כך ש
הוכיחו כי 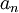 מתכנסת.
מתכנסת.
(רמז: יש בשאלה הזו קושי)
שאלה 2 (40 נק)
סעיף א
לכל שתי קבוצות לא ריקות וחסומות מלעיל.
- 1. הוכיחו/הפריכו:
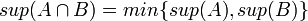
- 2. הוכיחו/הפריכו:
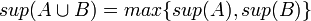
- 1. הוכיחו/הפריכו:
פתרון:
1) לא נכון. ניקח 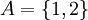 ו
ו 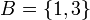
אז 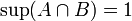
אבל 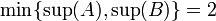
2) נכון.
בלי הגבלת כלליות נניח ש 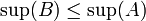 ולכן
ולכן 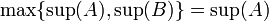
נסמן 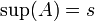 .
.
נוכיח ש 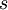 מקיים את שתי התכונות של
מקיים את שתי התכונות של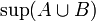
תכונה א) חסם מלעיל: יהי 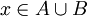 . אם
. אם 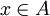 אז בוודאי
אז בוודאי
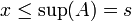
ואם 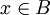 אז
אז
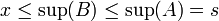
ולכן 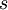 אכן חסם מלעיל של
אכן חסם מלעיל של 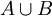
תכונה ב) חסם מלעיל הכי קטן: נניח ש 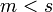 (צריך להראות ש
(צריך להראות ש 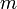 אינו חסם מעליל של
אינו חסם מעליל של 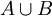 )
)
היות ש 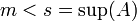 אז קיים
אז קיים 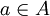 כך ש
כך ש 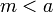 (לפי תכונה של חסם עליון של
(לפי תכונה של חסם עליון של  )
)
אבל בוודאי 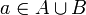 כלומר קיים איבר
כלומר קיים איבר 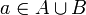 כך ש
כך ש 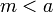 ולכן
ולכן 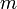 אינו חסם מלעיל של
אינו חסם מלעיל של 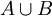 כנדרש.
כנדרש.
אכן הוכחנו כי 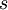 חסם עליון של
חסם עליון של 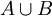 . ובזה סיימנו.
. ובזה סיימנו.
סעיף ב
נניח 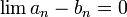 .
.
- הוכיחו/הפריכו:
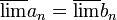
- הוכיחו/הפריכו:
פתרון: הטענה נכונה.
תהי 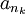 תת סדרה של
תת סדרה של 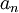 כך ש
כך ש
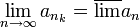
(הרי יש תת סדרה שמתכנסת לגבול העליון)
היות ש 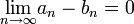 ,
,
אז כמובן ש
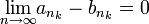
(כי תת סדרה של סדרה מתכנסת, מתכנסת לאותו מספר).
ולכן
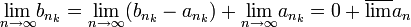
כלומר 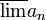 הוא גם גבול חלקי של
הוא גם גבול חלקי של 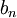 ולכן
ולכן
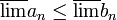 (כי
(כי 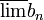 הוא הגבול החלקי הגדול ביותר)
הוא הגבול החלקי הגדול ביותר)
בדרך דומה מוכיחים
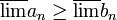
ולכן
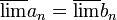
כנדרש
שאלה 3 (30 נק)
סעיף א
תהי סדרה המוגדרת ע"י כלל הנסיגה
הוכיחו כי הסדרה מתכנסת ומצאו את גבולה
(בכתיבה)
נרצה להוכיח כי הסדרה מונוטונית עולה וחסומה.
ראשית נוכיח שהסדרה חיובית (מה שדי ברור). למען הדיוק נוכיחזאת באופן מסודר באינדוקציה.
כלומר רוצים להוכיח ש 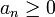 .
.
עבור 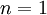 אכן
אכן 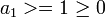 .
.
1) מונוטונית עולה: צריך להראות ש עיבוד הנוסחה נכשל (פונקציה \geqa לא מוכרת): a_{n+1}\geqa_n
עבור: 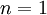 זה אכן נכון כי
זה אכן נכון כי
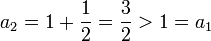
נניח שהטענה הכונה עבור  כלומר: עיבוד הנוסחה נכשל (פונקציה \geqa לא מוכרת): a_{n+1}\geqa_n
כלומר: עיבוד הנוסחה נכשל (פונקציה \geqa לא מוכרת): a_{n+1}\geqa_n
נוכיח עבור 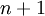 כלומר נוכיח כי
כלומר נוכיח כי
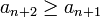
זה נכון מפני ש
עיבוד הנוסחה נכשל (שגיאת תחביר): a_{n+2}=\frac
סעיף ב
קבעו אם הטורים הבאים מתכנסים