הבדלים בין גרסאות בדף "88-165 תשעב סמסטר ב/תקצירי הרצאות"

גרסה מ־19:44, 1 במאי 2012

תקצירי הרצאות

תוכן עניינים

1 הרצאה ראשונה
2 הרצאה שניה
3 הרצאה שלישית
4 הרצאה רביעית
5 הרצאה חמישית
6 הרצאה שישית
7 הרצאה שביעית
8 הרצאה שמינית
9 הרצאה תשיעית
10 הרצאה עשירית
11 הרצאה אחת-עשרה

הרצאה ראשונה

(פרק 1, סעיף 1.2).

כל נתון סטטיסטי משמעותי אפשר לתאר על-ידי משתנים סטטיסטיים. נגענו קלות בטיפוסים של משתנים (משתנה איכותי, שבו אפשר רק לתאר את ההתפלגות; משתנה אורדינלי, שבו יש משמעות לסדר אבל לא לערך המספרי; משתנה אינטרוולי שבו יש משמעות גם להפרש המספרי, ומשתנה מנתי שבו יש בנוסף גם משמעות ליחס בין ערכים). דיברנו על הצגה גרפית של נתונים והנטיה הלא מוסברת של עורכי עיתונים להטעות באמצעותה.

למדנו כמה מדדי מרכז: ממוצע, שכיח, חציון, אמצע הטווח; וכמה מדדי פיזור: סטיית התקן, הטווח, הטווח הבין-רבעוני.

לצורך השוואה בין שני משתנים הצגנו את מקדם המתאם, שערכו תמיד בין 1 ל- 1-. כשהמשתנים בלתי תלויים, מקדם המתאם שלהם קרוב לאפס ("קרוב" ולא "שווה" משום שמדובר במדגם אקראי ולא באוכלוסיה כולה).

הרצאה שניה

(סעיף 1.3 - קומבינטוריקה).

מספר הדרכים לסדר n עצמים שונים בשורה הוא 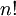$\,n!$ . מספר תת-הקבוצות של קבוצה בגודל n הוא 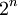$\ 2^n$ . מספר תת-הקבוצות בגודל k של קבוצה בגודל n הוא המקדם הבינומי n-מעל-k. זהו מספר הדרכים לבחור בלי החזרה, כשאין חשיבות לסדר. את המקדם הבינומי אפשר להכליל ל"מקדם מולטינומי", הסופר כמה דרכים יש לפרק קבוצה בגודל n לתת-קבוצות בגדלים 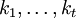$\ k_1,\dots,k_t$ , כאשר סכום הגדלים שווה ל-n.

כשיש חשיבות לסדר, מספר הדרכים לבחור k עצמים עם החזרה, מתוך n, הוא החזקה 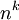$\ n^k$ . מספר הדרכים לבחור בלי החזרה הוא 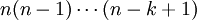$\ n(n-1)\cdots (n-k+1)$ (מה קורה אם k>n?). מספר הדרכים לבחור k עצמים מתוך n, עם החזרה, כשאין חשיבות לסדר, שווה למספר הפתרונות החיוביים למשוואה 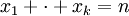$\ x_1+\cdot+x_k=n$ , שהוא המקדם הבינומי n+k-1 מעל n (זהו למעשה מספר ההתפלגויות האפשריות, עם x_i עצמים מסוג i).

למדנו (והוכחנו) את עקרון ההכלה וההדחה, 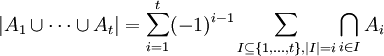$\ |A_1 \cup \cdots \cup A_t| = \sum_{i=1}^{t} (-1)^{i-1} \sum_{I \subseteq \{1,\dots,t\}, |I|=i} \bigcap_{i\in I}A_i$ .

הרצאה שלישית

(סעיף 2.1 - מרחבי הסתברות בדידים)

הגדרנו: מרחב הסתברות הוא זוג סדור, הכולל את קבוצת המצבים (שהיא סופית או בת-מניה), ופונקציה מהקבוצה הזו למספרים הממשיים שסכום כל ערכיה הוא 1. תת-קבוצות של מרחב ההסתברות נקראות "מאורעות". את הפונקציה 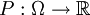$\ P : \Omega \rightarrow \mathbb{R}$ אפשר להמשיך לפונקציה 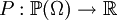$\ P : \mathbb{P}(\Omega) \rightarrow \mathbb{R}$ , המוגדרת על כל המאורעות. לערך 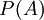$\ P(A)$ קוראים "ההסתברות של A". פונקציה זו מקיימת שתי תכונות חשובות: ההסתברות של המרחב כולו היא 1; וההסתברות של איחוד זר של מאורעות שווה לסכום ההסתברויות. את התכונה האחרונה הוכחנו במפורש, על-ידי חסימת ההפרש בין שני הסכומים בכל אפסילון חיובי.

תרגמנו את עקרון ההכלה וההדחה לשפת ההסתברות.

הגדרנו הסתברות מותנית 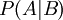$\ P(A|B)$ והוכחנו את נוסחת ההסתברות השלמה.

הרצאה רביעית

פתרנו את "בעיית המזכירה המבולבלת" בעזרת עקרון ההכלה וההדחה. הגדרנו מאורעות בלתי תלויים, והוכחנו כמה תכונות שקולות. הגדרנו אי-תלות משותפת של כמה מאורעות, והראינו שאי-תלות משותפת של שלושה מאורעות חזקה ממש מאי-תלות של כל זוג בנפרד.

הרצאה חמישית

הגדרנו משתנה מקרי, כפונקציה (כלשהי) ממרחב הסתברות בדיד (כלשהו) אל המספרים הממשיים. כדי לתאר משתנה מקרי X יש לדעת את ההתפלגות שלו, כלומר הפונקציה המתאימה לכל a את ההסתברות 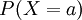$\ P(X=a)$ . ראינו שאם מפעילים פונקציה על משתנה מקרי, מתקבל משתנה מקרי חדש, שאפשר לחשב את ההתפלגות שלו מן ההתפלגות של המשתנה הראשון.

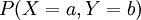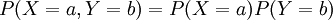טיפלנו בהתפלגות משותפת של זוג משתנים מקריים X,Y (המוגדרים על אותו מרחב הסתברות), שהיא הפונקציה המתאימה לכל a,b את ההסתברות $\ P(X=a,Y=b)$ . מן ההתפלגות המשותפת אפשר לשחזר את ההתפלגות של כל משתנה בנפרד. לסיכום הגדרנו מתי שני משתנים מקריים הם בלתי תלויים: אם לכל a,b מתקיים $\ P(X=a,Y=b) = P(X=a)P(Y=b)$ .

הרצאה שישית

הגדרנו את התוחלת של משתנה מקרי - מעין ממוצע משוכלל (וגם משוקלל) של הערכים שהמשתנה יכול לקבל. אם הנקודות של המרחב הן בעלות אותה הסתברות ("התפלגות אחידה"), אז התוחלת שווה לממוצע של ערכי המשתנה. התוחלת היא הומוגנית (ממעלה ראשונה) ואדיטיבית: 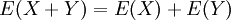$\ E(X+Y)=E(X)+E(Y)$ , וזאת לכל שני משתנים מקריים. תכונה חשובה זו מאפשרת לחשב תוחלות באמצעות פירוק המשתנה לסכום של משתנים פשוטים יותר, כגון משתנים מציינים של מאורעות במרחב.

אם X,Y שני משתנים מקריים, X|Y=b (קרי "X בהנתן Y=b") הוא משתנה מקרי, שההתפלגות שלו תלויה בערך של b. אפשר לקצר ולומר ש-X|Y הוא משתנה מקרי, שההתפלגות שלו תלויה ב-Y. למשתנה הזה יש תוחלת, (E(X|Y, שהיא פונקציה של Y. הוכחנו את חוק התוחלת החוזרת 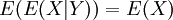$\ E(E(X|Y))=E(X)$ .

הרצאה שביעית

כדי לנתח את התוחלת של מכפלות, הגדרנו את השונות המשותפת של שני משתנים: 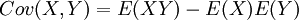$\ Cov(X,Y) = E(XY)-E(X)E(Y)$ . זוהי פונקציה סימטרית, הומוגנית ואדיטיבית בשני הרכיבים. אם X,Y בלתי תלויים, אז מחוק התוחלת החוזרת נובע ש- 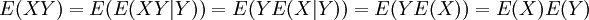$\ E(XY)=E(E(XY|Y))=E(YE(X|Y))=E(YE(X))=E(X)E(Y)$ , כלומר, השונות המשותפת שלהם היא אפס. משתנים כאלה נקראים בלתי מתואמים (כל שני משתנים בלתי תלויים הם בלתי מתואמים, אבל ההיפך נכון רק במקרה המיוחד שבו כל אחד משני המשתנים יכול לקבל רק שני ערכים).

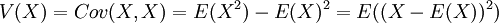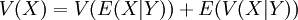השונות של משתנה מקרי X מוגדרת כשונות המשותפת שלו עם עצמו: $\ V(X)=Cov(X,X)=E(X^2)-E(X)^2=E((X-E(X))^2)$ . זהו גודל חיובי, השווה לאפס רק אם המשתנה קבוע (בהסתברות 1). השונות היא פונקציה הומוגנית (מדרגה 2). כאנלוגיה לחוק התוחלת החוזרת, הוכחנו את נוסחת פירוק השונות: $\ V(X)=V(E(X|Y))+E(V(X|Y))$ .

הרצאה שמינית

למדנו את ההתפלגויות (הבדידות) הקלאסיות:

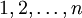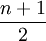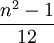ההתפלגות האחידה על המספרים $\ 1,2,\dots,n$ , שאותה מסמנים בסימון $\ X \sim U[1,n]$ . למשל, הערך שמתקבל מזריקת קוביה הוגנת מתפלג $\ U[1,6]$ , ואילו ספרה אקראית X מקיימת $\ X+1 \sim U[1,10]$ . התוחלת של משתנה כזה היא $\ \frac{n+1}{2}$ , והשונות $\ \frac{n^2-1}{12}$ .
התפלגות ברנולי: 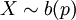$\ X \sim b(p)$ , שבה X מקבל רק את הערכים 0 (בהסתברות q=1-p) או p. התוחלת שווה לפרמטר p, והשונות היא pq. כל משתנה מקרי המקבל רק שני ערכים אפשר להביא (על-ידי העתקה לינארית) לצורה כזו. לדוגמא, אם X מקבל את הערכים אחד ומינוס אחד, אז 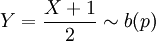$\ Y = \frac{X+1}{2} \sim b(p)$ עבור p מתאים.
התפלגות בינומית: 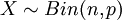$\ X \sim Bin(n,p)$ היא ההתפלגות של המשתנה הסופר כמה הצלחות יש בסדרה של n "ניסויי ברנולי" (ניסויים בלתי תלויים, שהסיכוי להצלחה בכל אחד מהם הוא קבוע, p). התוחלת של משתנה כזה היא np, והשונות npq (ההוכחה הקלה ביותר היא דרך משתנים מציינים).
התפלגות פואסון: 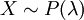$\ X \sim P(\lambda)$ , המוגדרת כך ש- 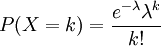$\ P(X=k) = \frac{e^{-\lambda}\lambda^k}{k!}$ . התוחלת והשונות הן 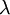$\ \lambda$ . התפלגות זו מופיעה כקירוב להתפלגות בינומית (אם 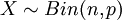$\ X \sim Bin(n,p)$ , ו-n גדול, אז בקירוב טוב 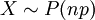$\ X \sim P(np)$ ), וגם בספירת תופעות לאורך זמן. את עניין ספירת התופעות לאורך זמן נסביר כשנלמד את ההתפלגות המעריכית (הרציפה).
התפלגות גאומטרית: 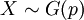$\ X \sim G(p)$ היא ההתפלגות של מספר הניסויים שיש לערוך עד להצלחה ראשונה (בסדרה של ניסויי ברנולי). הערך של משתנה זה אינו חסום, אם כי ההסתברות לערכים גדולים הולכת ודועכת (בקצב מעריכי). ההתפלגות הגאומטרית מיוחדת בתכונת חוסר הזכרון שלה: הידיעה שכבר נכשלו k ניסויים אינה מקרבת (ואינה מרחיקה) את ההצלחה הראשונה שתבוא.
התפלגות "בינומית שלילית": מספר הניסויים שאפשר לבצע (בסדרת ניסויי ברנולי) עד לכשלון ה-k. הפרמטרים הם k וההסתברות הקבועה, p.
התפלגות היפרגאומטרית: ההתפלגות של מספר הכדורים האדומים שמתקבלים כשמוציאים n כדורים (ללא החזרה!) מכד שבו A כדורים אדומים ו-B כדורים כחולים.

הרצאה תשיעית

בין ההתפלגויות השונות יש קשרים רבים, גם מעבר למובן מאליו (משתנה בינומי מוגדר כסכום של n משתנים מקריים ברנוליים בלתי-תלויים; משתנה "בינומי שלילי" אפשר להגדיר כסכום של משתנים מקריים גאומטריים). למשל:

אם X,Y משתנים בינומיים בלתי תלויים עם אותו p (אבל n-ים שונים), אז X+Y בינומי (עם אותו p), משום שהוא סופר את כל ההצלחות בסדרה ראשונה ואחר-כך בסדרה שניה של ניסויים.
אם X,Y משתני פואסון ב"ת, סכומם פואסוני (עם תוחלת השווה לסכום התוחלות, מה שאפשר לתרגם לחישוב הפרמטר, שהוא סכום הפרמטרים של X,Y).
במקרה הקודם, ההתפלגות של X בהנתן X+Y היא בינומית.
אם N הוא מספר ההתפרקויות של חלקיקים רדיואקטיביים במבחנה לאורך 25 דקות (משתנה פואסוני), ו-X הוא מספר ההתפרקויות שבהן התוצרים פגעו בלוחית המדידה (תופעה שהסיכוי לה הוא p, כלומר X בהנתן N מתפלג בינומית), אז X הוא משתנה פואסוני.
אם X,Y משתנים מקריים גאומטריים, אז ההתפלגות של X בהנתן X=Y היא עדיין גאומטרית (הראו כמה קל למצוא את הפרמטר אם העובדה הזו על התפלגות X בהנתן X=Y ידועה!)

דוגמאות חשובות אחרות מתקבלות משאיפה לגבול.

כאשר X מתפלג בינומית ו-n גדל תוך שהמכפלה np נשארת קבועה, ההתפלגות הולכת ומתקרבת להתפלגות פואסון עם הפרמטר np.
בהתפלגות היפרגאומטרית, אם מגדילים את A,B תוך שמירה על היחס A:B, התהליך הולך ונעשה דומה לדגימה עם החזרה (משום שכשיש בכד המוני כדורים, ממילא הסיכוי לחזרה על אותו כדור הוא זניח), ואז המשתנה ההיפרגאומטרי נעשה בקירוב בינומי.

הרצאה עשירית

מעבר להתפלגויות הקלאסיות, חשוב לדעת גם לטפל בתופעות שבהן חישוב ישיר הוא מסובך או בלתי אפשרי, כדי לקבל קירוב להתנהגות שלהן. בחנו מקרוב את הדוגמא המפורסמת של "פרדוקס יום ההולדת": הסיכוי שבין 23 אנשים יהיו שניים שנולדו באותו יום בשנה הוא מעט יותר מחצי, למרות ש-23 "הרבה יותר קטן" מ-365. ההסבר הוא בחישוב הסיכוי לכך שאין התנגשויות בבחירה אקראית של ימי ההולדת: מתברר שהסיכוי הזה יורד בקצב קרוב ל- 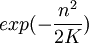$\ exp(-\frac{n^2}{2K})$ כאשר n הוא מספר האנשים (כאן 23) ו-K גודל המרחב שבו הם בוחרים.

בדרך כלל קל יותר לחשב תוחלות מאשר הסתברויות (במיוחד אם מדובר במשתנה שאפשר לפרק לסכום של משתנים מציינים רבים). גם לגבי ימי הולדת, קל לחשב שתוחלת מספר ההתנגשויות (כלומר, זוגות של אנשים שנולדו באותו יום) היא 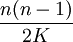$\ \frac{n(n-1)}{2K}$ , כך שמספר ההתנגשויות עולה באופן ריבועי עם מספר האנשים, וכאשר n הוא מסדר הגודל של 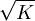$\ \sqrt{K}$ אפשר כבר לצפות להתנגשויות. דיברנו גם על המשתנה של זמן ההמתנה (להתנגשות הראשונה), שגם התוחלת שלו - שאותה לא חישבנו - פרופורציונלית לשורש גודל המרחב.

את הנימוקים האלה אפשר להפוך על ראשם כדי להעריך את גודל המרחב (כשזה אינו ידוע). אם המחשב בוחר מספרים באקראי ואחרי 979 צעדים מופיע לראשונה אותו מספר בפעם השניה, סביר להעריך שגודל המרחב הוא כ- 979 בריבוע, היינו כמליון.

טכניקת הפירוק לסכום של משתנים מציינים מאפשרת לתאר את המבנה של גרף מקרי (שבו יש n קודקודים, וכל אחת מ-n-מעל-2 הקשתות הפוטנציאליות מתממשת בהסתברות p, באופן בלתי תלוי).

הרצאה אחת-עשרה

הכנה לרציף.

@@ שורה 80: / שורה 80: @@
 === הרצאה עשירית ===
-מעבר להתפלגויות הקלאסיות, חשוב לדעת גם לטפל בתופעות שבהן חישוב ישיר הוא מסובך או בלתי אפשרי, כדי לקבל קירוב להתנהגות שלהן. בחנו מקרוב את הדוגמא המפורסמת של "פרדוקס יום ההולדת": הסיכוי שבין 23 אנשים יהיו שניים שנולדו באותו יום בשנה הוא מעט יותר מחצי, למרות ש-23 "הרבה יותר קטן" מ-365. ההסבר הוא בחישוב הסיכוי לכך שאין התנגשויות בבחירה אקראית של ימי ההולדת: מתברר שהסיכוי הזה יורד בקצב קרוב ל- <math>\ exp(-\frac{n^2}{2K}}</math> כאשר n הוא מספר האנשים (כאן 23) ו-K גודל המרחב שבו הם בוחרים.
+מעבר להתפלגויות הקלאסיות, חשוב לדעת גם לטפל בתופעות שבהן חישוב ישיר הוא מסובך או בלתי אפשרי, כדי לקבל קירוב להתנהגות שלהן. בחנו מקרוב את הדוגמא המפורסמת של "פרדוקס יום ההולדת": הסיכוי שבין 23 אנשים יהיו שניים שנולדו באותו יום בשנה הוא מעט יותר מחצי, למרות ש-23 "הרבה יותר קטן" מ-365. ההסבר הוא בחישוב הסיכוי לכך שאין התנגשויות בבחירה אקראית של ימי ההולדת: מתברר שהסיכוי הזה יורד בקצב קרוב ל- <math>\ exp(-\frac{n^2}{2K})</math> כאשר n הוא מספר האנשים (כאן 23) ו-K גודל המרחב שבו הם בוחרים.
 בדרך כלל קל יותר לחשב תוחלות מאשר הסתברויות (במיוחד אם מדובר במשתנה שאפשר לפרק לסכום של משתנים מציינים רבים). גם לגבי ימי הולדת, קל לחשב שתוחלת מספר ההתנגשויות (כלומר, זוגות של אנשים שנולדו באותו יום) היא <math>\ \frac{n(n-1)}{2K}</math>, כך שמספר ההתנגשויות עולה באופן ריבועי עם מספר האנשים, וכאשר n הוא מסדר הגודל של <math>\ \sqrt{K}</math> אפשר כבר לצפות להתנגשויות. דיברנו גם על המשתנה של זמן ההמתנה (להתנגשות הראשונה), שגם התוחלת שלו - שאותה לא חישבנו - פרופורציונלית לשורש גודל המרחב.
@@ שורה 86: / שורה 86: @@
 את הנימוקים האלה אפשר להפוך על ראשם כדי להעריך את גודל המרחב (כשזה אינו ידוע). אם המחשב בוחר מספרים באקראי ואחרי 979 צעדים מופיע לראשונה אותו מספר בפעם השניה, סביר להעריך שגודל המרחב הוא כ- 979 בריבוע, היינו כמליון.
 טכניקת הפירוק לסכום של משתנים מציינים מאפשרת לתאר את המבנה של גרף מקרי (שבו יש n קודקודים, וכל אחת מ-n-מעל-2 הקשתות הפוטנציאליות מתממשת בהסתברות p, באופן בלתי תלוי).
 === הרצאה אחת-עשרה ===
 הכנה לרציף.

הבדלים בין גרסאות בדף "88-165 תשעב סמסטר ב/תקצירי הרצאות"

גרסה מ־19:44, 1 במאי 2012

תוכן עניינים

הרצאה ראשונה

הרצאה שניה

הרצאה שלישית

הרצאה רביעית

הרצאה חמישית

הרצאה שישית

הרצאה שביעית

הרצאה שמינית

הרצאה תשיעית

הרצאה עשירית

הרצאה אחת-עשרה

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים