הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 2"

מתוך Math-Wiki
קפיצה אל: ניווט, חיפוש
(←‏יחסים)
(←‏פתרון)
שורה 29: שורה 29:
  
 
לכן, ניתן להגדיר זוג סדור על ידי קבוצות בלבד (באופן דומה לכך שכל המתמטיקה פחות או יותר נבנת על קבוצות בלבד).
 
לכן, ניתן להגדיר זוג סדור על ידי קבוצות בלבד (באופן דומה לכך שכל המתמטיקה פחות או יותר נבנת על קבוצות בלבד).
 +
 +
 +
===תרגיל===
 +
הוכח שלכל קבוצות A,B,C מתקיים <math>A\times(B\cap C)=(A\times B)\cap(A\times C)</math>
 +
 +
====פתרון====
 +
<math>(x,y)\in A\times(B\cap C) \iff (x\in A) \and [(y\in B)\and (y\in C)] \iff [(x\in A)\and(y\in B)] \and [(x\in A)\and(y\in B)] \iff x\in[(A\times B)\cap(A\times C)]</math>

גרסה מ־18:54, 25 ביולי 2011

יחסים

הגדרה: המכפלה הקרטזית של שתי קבוצות A וB הינה אוסף כל הזוגות הסדורים - 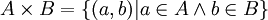A\times B = \{(a,b)|a\in A \and b\in B\}. ההבדל בין זוג סדור לבין קבוצה המכילה זוג איברים היא שהאיברים יכולים להיות שווים בזוג סדור, והסדר שלהם מהותי. כלומר שני האיברים הבאים שונים 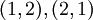(1,2),(2,1) והאיבר הבא הינו זוג חוקי (1,1).

ניתן להכליל את ההגדרה לעיל לn-יה סדורה - כלומר n איברים מסודרים.

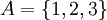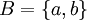דוגמא: A=\{1,2,3\} וB=\{a,b\} אזי מתקיים A\times B =\{(1,a),(2,a),(3,a),(1,b),(2,b),(3,b)\}


ניתן להגדיר זוגות סדורים באמצעות הגדרת הקבוצות בלבד, כפי שנראה בתרגיל הבא:

תרגיל

הוכח/הפרך:

1. [(a=c)\and(b=d)]\iff \{\{a\},b\}=\{\{c\},d\}

2. [(a=c)\and(b=d)]\iff \{\{a\},\{a,b\}\}=\{\{c\},\{c,d\}\}

פתרון

1. הפרכה ע"י הדוגמא הנגדית 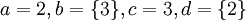a=2,b=\{3\},c=3,d=\{2\}


2.

הוכחה: הכיוון משמאל לימין הוא ברור. מימין לשמאל, נניח והקבוצות שוות אזי 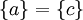\{a\}=\{c\} או ש \{a\}=\{c,d\}.

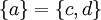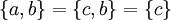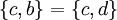במקרה הראשון, נובע a=c ובמקרה השני נובע a=c=d, כך או כך a=c. כעת, \{a,b\}=\{c,b\}=\{c\} או \{c,b\}=\{c,d\} ונובע משניהם ש b=d.


לכן, ניתן להגדיר זוג סדור על ידי קבוצות בלבד (באופן דומה לכך שכל המתמטיקה פחות או יותר נבנת על קבוצות בלבד).


תרגיל

הוכח שלכל קבוצות A,B,C מתקיים 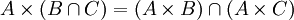A\times(B\cap C)=(A\times B)\cap(A\times C)

פתרון

(x,y)\in A\times(B\cap C) \iff (x\in A) \and [(y\in B)\and (y\in C)] \iff [(x\in A)\and(y\in B)] \and [(x\in A)\and(y\in B)] \iff x\in[(A\times B)\cap(A\times C)]

מקור: https://math-wiki.com/index.php?title=88-195_בדידה_לתיכוניסטים_תשעא/מערך_שיעור/שיעור_2&oldid=11679