הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 5"
אחיה בר-און (שיחה | תרומות) (←המשך פונקציות) |
אחיה בר-און (שיחה | תרומות) (←המשך פונקציות) |
||
| שורה 26: | שורה 26: | ||
נראה את ההכלה בכיוון השני אם <math>f</math> חח"ע: | נראה את ההכלה בכיוון השני אם <math>f</math> חח"ע: | ||
| + | |||
יהא <math>x\in f^{-1}(f(A))</math> לכן <math>f(x) \in f(A)</math> לכן <math>\exists a\in A : f(x)=f(a)</math>. כיוון ש <math>f</math> חח"ע נובע כי <math>x=a\in A</math> | יהא <math>x\in f^{-1}(f(A))</math> לכן <math>f(x) \in f(A)</math> לכן <math>\exists a\in A : f(x)=f(a)</math>. כיוון ש <math>f</math> חח"ע נובע כי <math>x=a\in A</math> | ||
| + | |||
| + | |||
| + | '''תרגיל.''' | ||
| + | תהי <math>f:X\rightarrow Y</math> ותהי <math>A\subseteq Y</math>. הוכח <math> f(f^{-1}(A)) \subseteq A</math>. וקיים שיוויון אם <math>f</math> על | ||
| + | |||
| + | '''פתרון.''' | ||
| + | |||
| + | יהא <math>f(x) \in f(f^{-1}(A))</math> כאשר <math>x\in f^{-1}(A)</math> ולכן <math> f(x)\in A </math>. | ||
| + | |||
| + | נראה את ההכלה בכיוון השני אם <math>f</math> על: | ||
| + | |||
| + | יהא <math> a\in A </math> כיוון ש f על <math>\exists x\in X : f(x)=a </math> לכן <math> x\in \in f^{-1}(A) </math>. ואז <math>a=f(x)\in f(f^{-1}(A)) </math> | ||
| שורה 45: | שורה 58: | ||
2. ''' f חח"ע אמ"מ g על ''' | 2. ''' f חח"ע אמ"מ g על ''' | ||
בכיוון אחד- נתון f חח"ע. אזי <math>g(f(A))=f^{-1}(f(A))=A</math> ולכן g על ( עבור A המקור שלה יהיה <math>f(A)</math> ) | בכיוון אחד- נתון f חח"ע. אזי <math>g(f(A))=f^{-1}(f(A))=A</math> ולכן g על ( עבור A המקור שלה יהיה <math>f(A)</math> ) | ||
| + | |||
בכיוון השני- נתון g על. נניח בשלילה ש f אינה חח"ע אזי קיימים <math>x,y \in X</math> שונים כך ש <math>f(x)=f(y)</math>. נביט בנקודון <math>A=\{x\}</math> כיוון ש g כלקיימת <math>B\in P(Y)</math> | בכיוון השני- נתון g על. נניח בשלילה ש f אינה חח"ע אזי קיימים <math>x,y \in X</math> שונים כך ש <math>f(x)=f(y)</math>. נביט בנקודון <math>A=\{x\}</math> כיוון ש g כלקיימת <math>B\in P(Y)</math> | ||
כך ש <math>f^{-1}(B)=g(B)=A</math> לכן <math>B\subseteq f(f^{-1}(B)) = f(A)= \{f(x)\} </math> כיוון ש B אינה ריקה נקבל ש <math>B=\{f(x)\} </math> | כך ש <math>f^{-1}(B)=g(B)=A</math> לכן <math>B\subseteq f(f^{-1}(B)) = f(A)= \{f(x)\} </math> כיוון ש B אינה ריקה נקבל ש <math>B=\{f(x)\} </math> | ||
גרסה מ־19:37, 25 ביולי 2013
המשך פונקציות
הגדרה. תהי  פונקציה, ויהיו תת קבוצות
פונקציה, ויהיו תת קבוצות 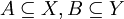 . אזי
. אזי 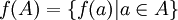 ,
, 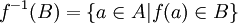 .
.
שימו לב שהסימון 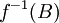 אינו רומז בשום צורה שהפונקציה צריכה להיות הפיכה, הגדרה זו תקפה לכל פונקציה.
אינו רומז בשום צורה שהפונקציה צריכה להיות הפיכה, הגדרה זו תקפה לכל פונקציה.
תרגיל.
הוכח/הפרך: תהא 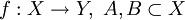 אזי
אזי 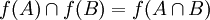
פתרון.
נניח וf אינה חח"ע, כלומר קיימים 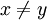 כך ש
כך ש 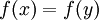 . ניקח
. ניקח 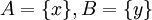 אזי:
אזי:
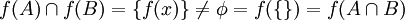
תרגיל.
תהי  ותהי
ותהי 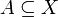 . הוכח
. הוכח 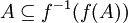 . וקיים שיוויון אם
. וקיים שיוויון אם  חח"ע
חח"ע
פתרון.
יהא 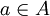 אזי
אזי 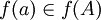 ולכן
ולכן 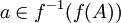 .
.
נראה את ההכלה בכיוון השני אם  חח"ע:
חח"ע:
יהא 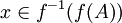 לכן
לכן 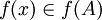 לכן
לכן 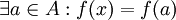 . כיוון ש
. כיוון ש  חח"ע נובע כי
חח"ע נובע כי 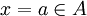
תרגיל.
תהי  ותהי
ותהי 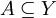 . הוכח
. הוכח 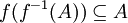 . וקיים שיוויון אם
. וקיים שיוויון אם  על
על
פתרון.
יהא 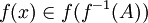 כאשר
כאשר 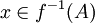 ולכן
ולכן  .
.
נראה את ההכלה בכיוון השני אם  על:
על:
יהא 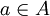 כיוון ש f על
כיוון ש f על 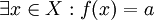 לכן
לכן 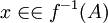 . ואז
. ואז 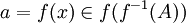
תרגיל ממבחן (קצת משודרג).
יהיו 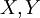 שתי קבוצות, ותהי
שתי קבוצות, ותהי  פונקציה כלשהי. נגדיר את הפונקציה
פונקציה כלשהי. נגדיר את הפונקציה 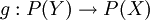 על ידי
על ידי 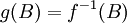 .
בדוק את הקשר בין החח"ע/על של f לבין אלה של g. (כלומר, מה גורר את מה בהכרח).
.
בדוק את הקשר בין החח"ע/על של f לבין אלה של g. (כלומר, מה גורר את מה בהכרח).
פתרון.
1. f על אמ"מ g חח"ע
בכיוון אחד- נתון ש f על. נניח 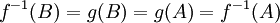 נפעיל את f על שני הצדדים ונקבל (בגלל ש f על)
נפעיל את f על שני הצדדים ונקבל (בגלל ש f על) 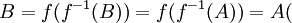
בכיוון השני- נתון כי g חח"ע. נניח בשלילה כי f אינה על אזי 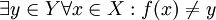 לכן
לכן 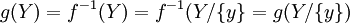 בסתירה לחח"ע של g.
בסתירה לחח"ע של g.
2. f חח"ע אמ"מ g על
בכיוון אחד- נתון f חח"ע. אזי 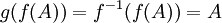 ולכן g על ( עבור A המקור שלה יהיה
ולכן g על ( עבור A המקור שלה יהיה 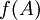 )
)
בכיוון השני- נתון g על. נניח בשלילה ש f אינה חח"ע אזי קיימים 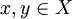 שונים כך ש
שונים כך ש 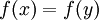 . נביט בנקודון
. נביט בנקודון 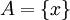 כיוון ש g כלקיימת
כיוון ש g כלקיימת 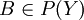 כך ש
כך ש 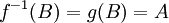 לכן
לכן 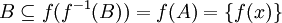 כיוון ש B אינה ריקה נקבל ש
כיוון ש B אינה ריקה נקבל ש 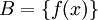 לכן
לכן 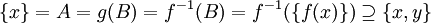 . ולכן
. ולכן  . סתירה.
. סתירה.
מכאן ניתן להסיק כי שאר הגרירות אינן מוכרחות:
- ייתכן ו-f חח"ע אך g אינה כזו (ניקח f חח"ע שאינה על אזי g אינה חח"ע לפי 1)
- יתכן ו-g חח"ע אך f אינה כזו. (ניקח g חח"ע שאינה על אזי f אינה חח"ע לפי 2)
- ייתכן ו-f על אך g אינה כזו (ניקח f על שאינה חח"ע אזי g אינה על לפי 2)
- ייתכן ו-g על אך f אינה כזו (ניקח g על שאינה חח"ע אזי f אינה על לפי 1)
אתם מוזמנים לתת דוגמאות למסקנות לעיל
למשל:
יהיו 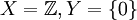 . אזי קיימת פונקציה f יחידה מX לY. פונקציה זו אינה חח"ע כמובן, אך g כן חח"ע שכן
. אזי קיימת פונקציה f יחידה מX לY. פונקציה זו אינה חח"ע כמובן, אך g כן חח"ע שכן 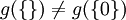 ואלה הקבוצות היחידות בקבוצת החזקה של Y.
ואלה הקבוצות היחידות בקבוצת החזקה של Y.
הגדרה.
תהי  ותהי
ותהי 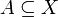 . הפונקציה f מצומצמת לA מוגדרת על ידי:
. הפונקציה f מצומצמת לA מוגדרת על ידי:  כך ש
כך ש 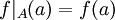 .
.
דוגמא.
נביט ב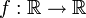 המוגדרת על ידי
המוגדרת על ידי 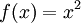 ואינה חח"ע. נכון לומר שהפונקציה המצומצמת
ואינה חח"ע. נכון לומר שהפונקציה המצומצמת 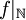 כן חח"ע.
כן חח"ע.
תרגיל.
תהי  פונקציה, הוכח שקיימת קבוצה A כך ש
פונקציה, הוכח שקיימת קבוצה A כך ש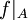 חח"ע
חח"ע
פתרון.
פייי זו שאלה קשה. תזכירו לנו אותה כאשר נגיע לאקסיומת הבחירה. (שכן נביט ב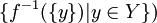 ונרצה לבחור איבר יחיד מבין כל קבוצה כזו. אקסיומת הבחירה היא זו המאפשרת לנו לבצע בחירה זו בשלום.)
ונרצה לבחור איבר יחיד מבין כל קבוצה כזו. אקסיומת הבחירה היא זו המאפשרת לנו לבצע בחירה זו בשלום.)
הגדרה. תהי 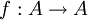 , ויהי R יחס שקילויות על A. אומרים כי f מוגדרת היטב על
, ויהי R יחס שקילויות על A. אומרים כי f מוגדרת היטב על 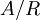 אם
אם 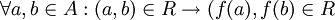
תרגיל מוטיבציה להגדרה לעיל.
המוטיבציה להגדרה הזו היא היכולת לגזור ממנה פונקציה על חבורת המנה. נגדיר יחס על חבורת המנה ![g=\{([a],[f(a)])|a\in A\}](/images/math/3/a/f/3af13d48c202bd1a70c19af62d07aad7.png) . נוכיח ש-g הינה חד-ערכית ולכן פונקציה.
. נוכיח ש-g הינה חד-ערכית ולכן פונקציה.
הוכחה
נניח וקיימים 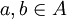 כך ש
כך ש ![[a]=[b]](/images/math/5/9/c/59cf3abe8a280a0de4a9dd1cfa304603.png) . לכן
. לכן 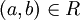 ולכן
ולכן 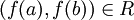 ולכן
ולכן ![[f(a)]=[f(b)]](/images/math/7/b/6/7b6043fa874b5980c7368d74a90d27c6.png) . לכן לא ייתכן מצב בו
. לכן לא ייתכן מצב בו 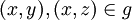 אבל
אבל 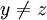 .
.
דוגמא.
האם הפונקציה f על הרציונאליים המוגדרת על ידי 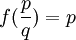 מוגדרת היטב?
מוגדרת היטב?
פתרון.
יש לשים לב שלא באמת הגדרנו את הפונקציה על הרציונאליים, אלא על אוסף הזוגות הסדורים של שלמים 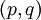 כך שהאיבר הימני שונה מאפס. נגדיר על קבוצה זו את יחס השקילויות R המוגדר על ידי
כך שהאיבר הימני שונה מאפס. נגדיר על קבוצה זו את יחס השקילויות R המוגדר על ידי 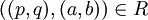 אם
אם 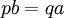 . נראה כי f אינה מוגדרת היטב בתנאים אלו:
. נראה כי f אינה מוגדרת היטב בתנאים אלו:
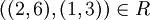 אולם
אולם 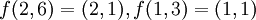 ו
ו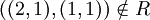 .
.
בכוונה ניסחנו את התרגיל באופן הרומז על יחס השקילויות מבלי לומר אותו במפורש. זו הדרך בה נתקל במושג 'מוגדר היטב' במהלך התואר - יחס השקילויות יהיה מרומז בלבד.