הבדלים בין גרסאות בדף "88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 5"
אחיה בר-און (שיחה | תרומות) (←המשך פונקציות) |
(←תרגיל) |
||
| (28 גרסאות ביניים של 7 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
'''[[מתמטיקה בדידה - מערך תרגול|חזרה למערכי התרגול]]''' | '''[[מתמטיקה בדידה - מערך תרגול|חזרה למערכי התרגול]]''' | ||
| − | ==המשך פונקציות== | + | ==המשך פונקציות - פונקציות על תת-קבוצות== |
| − | + | ===תמונות חלקיות=== | |
| − | + | '''הגדרה.''' תהי <math>f:X\rightarrow Y</math> פונקציה, ויהיו תת קבוצות <math>A\subseteq X,B\subseteq Y</math>. אזי '''התמונה החלקית של A תחת f''' היא התת-קבוצה <math>f(A)=\{f(a)|a\in A\}</math>, ו'''התמונה החלקית ההפוכה של B תחת f''' היא התת-קבוצה <math>f^{-1}(B)=\{a\in X|f(a)\in B\}</math>. | |
| + | שימו לב להבדל בין התמונה ההפוכה <math>f^{-1}(B)</math> לבין הפונקציה ההופכית <math>f^{-1}(y)</math>. התמונה ההפוכה איננה מניחה כי הפונקציה f הפיכה. הדרך להבחין בין פונקציה הפיכה לתמונה ההפוכה היא לבדוק האם בין הסוגריים נמצא ''איבר'' של התמונה (בדוגמאות לעיל זהו <math>y \in Y</math>) או שנמצאת ''תת-קבוצה'' של התמונה (בדוגמאות לעיל זו <math>B\subseteq Y</math>). | ||
| − | + | ==== דוגמאות ==== | |
| − | + | תהא <math>D:\mathbb{R}\to \mathbb{R}</math> פונקצית דריכלה. אזי <math>D(\mathbb{Q})=\{1\},D^{-1}(\{1\})=\mathbb{Q}=D^{-1}((0.5, 18))</math> | |
| + | |||
| + | תהא <math>f:X\to Y</math> פונקצית . אזי <math>f^{-1}(Y)=X</math> | ||
| + | |||
| + | תהא <math>f:\mathbb{R}\to \mathbb{Z}</math> פונקצית הערך השלם התחתון. אזי <math>f((-0.5,3/4))=\{-1,0\},f^{-1}(\{1\})=[1,2)</math> | ||
| + | |||
| + | |||
| + | ==== תכונות ==== | ||
| + | # אם <math>A_1\subseteq A_2</math> אזי <math>f(A_1)\subseteq f(A_2)</math> | ||
| + | # אם <math>B_1\subseteq B_2</math> אזי <math>f^{-1}(B_1)\subseteq f^{-1}(B_2)</math> | ||
| + | # הוכיחו/הפריכו טענות מקבילות עם משלים של קבוצות. | ||
| + | |||
| + | |||
| + | ==== תרגיל ==== | ||
| + | הוכיחו/הפריכו: תהי f פונקציה <math>f:X \to Y</math> ותהיינה <math>Z,W\subseteq X, A,B \subseteq Y</math>. אזי | ||
| + | # <math>f^{-1}[A]\cap f^{-1}[B]=f^{-1}[A\cap B]</math> | ||
| + | # <math>f^{-1}[A]\cup f^{-1}[B]=f^{-1}[A\cup B]</math> | ||
| + | # <math>f^{-1}[A\setminus B]=f^{-1}[A]\setminus f^{-1}[B]</math> | ||
| + | # <math>f^{-1}[A]\triangle f^{-1}[B]=f^{-1}[A\triangle B]</math> | ||
| + | # <math>f[Z]\triangle f[W]=f[Z\triangle W]</math> | ||
| + | |||
| + | פתרון: תחשבו. עדיף את שני האחרונים, כי הראשונים לפעמים נעשים בהרצאה. | ||
| + | |||
| + | ====תרגיל==== | ||
| + | הוכח/הפרך: תהיינה <math>A,B \subseteq X</math> ותהי f פונקציה <math>f:X \to Y</math>. אזי <math>f(A)\cap f(B)=f(A\cap B)</math> | ||
'''פתרון.''' | '''פתרון.''' | ||
| − | נניח וf אינה חח"ע, כלומר קיימים <math>x\neq y </math> כך ש <math>f(x)=f(y)</math>. ניקח <math>A=\{x\},B=\{y\}</math> אזי: | + | נפריך על ידי דוגמא נגדית. נניח וf אינה חח"ע, כלומר קיימים <math>x\neq y </math> כך ש <math>f(x)=f(y)</math>. ניקח <math>A=\{x\},B=\{y\}</math> אזי: |
<math>f(A)\cap f(B) = \{f(x)\} \neq \phi = f(\{\}) = f(A\cap B)</math> | <math>f(A)\cap f(B) = \{f(x)\} \neq \phi = f(\{\}) = f(A\cap B)</math> | ||
| + | '''הערה''' תמיד מתקיים <math>f(A\cap B)\subseteq f(A)\cap f(B)</math> | ||
| − | ''' | + | '''הערה''' הטענה נכונה אם <math>f</math> חח"ע. הוכיחו! |
| + | |||
| + | ===תרגיל (בהרצאה בד"כ)=== | ||
תהי <math>f:X\rightarrow Y</math> ותהי <math>A\subseteq X</math>. הוכח <math>A \subseteq f^{-1}(f(A))</math>. וקיים שיוויון אם <math>f</math> חח"ע | תהי <math>f:X\rightarrow Y</math> ותהי <math>A\subseteq X</math>. הוכח <math>A \subseteq f^{-1}(f(A))</math>. וקיים שיוויון אם <math>f</math> חח"ע | ||
| שורה 29: | שורה 57: | ||
יהא <math>x\in f^{-1}(f(A))</math> לכן <math>f(x) \in f(A)</math> לכן <math>\exists a\in A : f(x)=f(a)</math>. כיוון ש <math>f</math> חח"ע נובע כי <math>x=a\in A</math> | יהא <math>x\in f^{-1}(f(A))</math> לכן <math>f(x) \in f(A)</math> לכן <math>\exists a\in A : f(x)=f(a)</math>. כיוון ש <math>f</math> חח"ע נובע כי <math>x=a\in A</math> | ||
| + | דוגמא שלא מתקיים שיוויון <math>f:\{1,2\}\to \{1\}</math> (יש דרך אחת להגדיר את הפונקציה). אזי נגדיר <math>A=\{2\}</math> ומתקיים <math> f^{-1}(f(A))=\{1,2\}\neq A</math> | ||
| − | + | ===תרגיל (בXI)=== | |
תהי <math>f:X\rightarrow Y</math> ותהי <math>A\subseteq Y</math>. הוכח <math> f(f^{-1}(A)) \subseteq A</math>. וקיים שיוויון אם <math>f</math> על | תהי <math>f:X\rightarrow Y</math> ותהי <math>A\subseteq Y</math>. הוכח <math> f(f^{-1}(A)) \subseteq A</math>. וקיים שיוויון אם <math>f</math> על | ||
| שורה 41: | שורה 70: | ||
יהא <math> a\in A </math> כיוון ש f על <math>\exists x\in X : f(x)=a </math> לכן <math> x \in f^{-1}(A) </math>. ואז <math>a=f(x)\in f(f^{-1}(A)) </math> | יהא <math> a\in A </math> כיוון ש f על <math>\exists x\in X : f(x)=a </math> לכן <math> x \in f^{-1}(A) </math>. ואז <math>a=f(x)\in f(f^{-1}(A)) </math> | ||
| + | דוגמא שלא מתקיים שיוויון <math>f:\{1\}\to \{1,2\}</math> המוגדרת <math>1\mapsto 1</math>. אזי נגדיר <math>B=\{1,2\}</math> ומתקיים <math> f(f^{-1}(B)) =\{1\}\neq B</math>. | ||
| − | + | ===תרגיל ממבחן (קצת משודרג)=== | |
| − | + | ||
יהיו <math>X,Y</math> שתי קבוצות, ותהי <math>f:X\rightarrow Y</math> פונקציה כלשהי. נגדיר את הפונקציה <math>g:P(Y)\rightarrow P(X)</math> על ידי <math>g(B)=f^{-1}(B)</math>. | יהיו <math>X,Y</math> שתי קבוצות, ותהי <math>f:X\rightarrow Y</math> פונקציה כלשהי. נגדיר את הפונקציה <math>g:P(Y)\rightarrow P(X)</math> על ידי <math>g(B)=f^{-1}(B)</math>. | ||
| שורה 50: | שורה 79: | ||
'''פתרון.''' | '''פתרון.''' | ||
| − | 1. ''' f על אמ"מ g חח"ע ''' | + | 1. נמצא ב XI הטענה ''' f על אמ"מ g חח"ע ''' |
| − | בכיוון אחד- נתון ש f על. נניח <math>f^{-1}(B)=g(B)=g(A)=f^{-1}(A)</math> נפעיל את f על שני הצדדים ונקבל (בגלל ש f על) <math>B=f(f^{-1}(B))=f(f^{-1}(A))=A | + | בכיוון אחד- נתון ש f על. נניח <math>f^{-1}(B)=g(B)=g(A)=f^{-1}(A)</math> נפעיל את f על שני הצדדים ונקבל (בגלל ש f על) <math>B=f(f^{-1}(B))=f(f^{-1}(A))=A</math> |
| − | בכיוון השני- נתון כי g חח"ע. נניח בשלילה כי f אינה על אזי <math>\exists y\in Y\forall x\in X:f(x)\neq y</math> לכן <math>g(Y)=f^{-1}(Y)=f^{-1}(Y/\{y\}=g(Y/\{y\})</math> בסתירה לחח"ע של g. | + | בכיוון השני- נתון כי g חח"ע. נניח בשלילה כי f אינה על אזי <math>\exists y\in Y\forall x\in X:f(x)\neq y</math> לכן <math>g(Y)=f^{-1}(Y)=f^{-1}(Y/\{y\})=g(Y/\{y\})</math> בסתירה לחח"ע של g. |
| שורה 82: | שורה 111: | ||
למשל: | למשל: | ||
| − | יהיו <math>X=\mathbb{Z}, Y=\{0\}</math>. אזי קיימת פונקציה f יחידה מX לY. פונקציה זו אינה חח"ע כמובן, אך g כן חח"ע שכן <math>g(\{\})\neq g(\{0\})</math> ואלה הקבוצות היחידות בקבוצת החזקה של Y. | + | יהיו <math>X=\mathbb{Z}, Y=\{0\}</math>. אזי קיימת פונקציה f יחידה מX לY. פונקציה זו אינה חח"ע כמובן, אך g כן חח"ע שכן <math>g(\{\})\neq g(\{0\})</math> ואלה הקבוצות היחידות בקבוצת החזקה של Y. |
| + | ==== תרגיל (בהרצאה בד"כ) ==== | ||
| + | תהיינה A,B קבוצות לא ריקות. הוכיחו כי: | ||
| + | # אם קיימת <math>f:A\to B</math> חח"ע אזי קיימת <math>g:B\to A</math> על. | ||
| + | # אם A,B סופיות: קיימת <math>f:A\to B</math> חח"ע אמ"מ <math>|A|\leq |B|</math> | ||
| + | # אם A,B סופיות: קיימת <math>f:A\to B</math> על אמ"מ <math>|B|\leq |A|</math> | ||
| − | + | === פונקציות המכבדות יחס שקילות === | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
'''הגדרה.''' תהי <math>f:A\rightarrow B</math>, ויהי R יחס שקילויות על A. אומרים כי '''f מוגדרת היטב על <math>A/R</math>''' אם <math>\forall a,b\in A:(a,b)\in R\Rightarrow f(a)=f(b)</math> | '''הגדרה.''' תהי <math>f:A\rightarrow B</math>, ויהי R יחס שקילויות על A. אומרים כי '''f מוגדרת היטב על <math>A/R</math>''' אם <math>\forall a,b\in A:(a,b)\in R\Rightarrow f(a)=f(b)</math> | ||
| − | כלומר אם a שקול ל b אזי <math>f(a)=f(b)</math> | + | כלומר אם a שקול ל b אזי <math>f(a)=f(b)</math>. |
למה זה טוב? | למה זה טוב? | ||
| שורה 117: | שורה 133: | ||
הוכחה: | הוכחה: | ||
| − | 1. g שלמה - לפי העיניים | + | 1. g שלמה - "לפי העיניים". כלל ההתאמה מנוסח כך שהיחס הוא שלם. |
| − | 2. g חד ערכית- נניח <math>[a]=[b]</math> צ"ל <math> | + | 2. g חד ערכית- נניח <math>[a]=[b]</math>, צ"ל <math>g([a])=g([b])</math>. מהנתון ש <math>[a]=[b]</math> נובע ש <math>(a,b)\in R</math>, ולכן, לפי הגדרת f כמוגדרת היטב על קבוצת המנה, מתקיים <math>f(a)=f(b)</math>, ולפי הגדרת g מתקיים <math>g([a])=f(a)=f(b)=g([b])</math>. |
| + | ==== דוגמא ==== | ||
| + | נגדיר על השלמים יחס שקילות ע"י x~y אמ"מ y=x or y=-x. | ||
| − | + | בדקו מי מהבאות היא פונקציה מקבוצת המנה לשלמים: | |
| − | האם f על הרציונאליים המוגדרת על ידי <math>f(\frac{p}{q})=p</math> מוגדרת היטב? | + | # <math>\{([n]_{~},n): n\in \mathbb{Z} \}</math> |
| + | # <math>\{([n]_{~},n^2): n\in \mathbb{Z} \}</math> | ||
| + | |||
| + | ====דוגמא ==== | ||
| + | האם f על הרציונאליים המוגדרת על ידי <math>f\bigg(\frac{p}{q}\bigg)=p</math> מוגדרת היטב? | ||
'''פתרון''' | '''פתרון''' | ||
| − | לא! כזכור הרציונאליים הם קבוצת מנה של <math>\mathbb{Z}\times \mathbb{N}</math>. לפי היחס שהגדרנו מתקיים <math>\frac{1}{3}=\frac{2}{6}</math> אבל לא מתקיים <math>f(\frac{1}{3})=1\not=2=f(\frac{2}{6})</math> | + | לא! כזכור הרציונאליים הם קבוצת מנה של <math>\mathbb{Z}\times \mathbb{N}</math>. לפי היחס שהגדרנו מתקיים <math>\frac{1}{3}=\frac{2}{6}</math> אבל לא מתקיים <math>f\bigg(\frac{1}{3}\bigg)=1\not=2=f\bigg(\frac{2}{6}\bigg)</math> |
במילים: לא ברור לאן f שולחת את השבר שליש! | במילים: לא ברור לאן f שולחת את השבר שליש! | ||
הערה: בכוונה ניסחנו את התרגיל באופן הרומז על יחס השקילויות מבלי לומר אותו במפורש. זו הדרך בה נתקל במושג 'מוגדר היטב' במהלך התואר - יחס השקילויות יהיה מרומז בלבד. | הערה: בכוונה ניסחנו את התרגיל באופן הרומז על יחס השקילויות מבלי לומר אותו במפורש. זו הדרך בה נתקל במושג 'מוגדר היטב' במהלך התואר - יחס השקילויות יהיה מרומז בלבד. | ||
| + | |||
| + | ===פונקציה מצומצמת=== | ||
| + | |||
| + | '''הגדרה.''' | ||
| + | תהי <math>f:X\rightarrow Y</math> ותהי <math>A\subseteq X</math>. הפונקציה '''f מצומצמת לA''' מוגדרת על ידי: <math>f|_A:A\rightarrow Y</math> כך ש-<math>f|_A(a)=f(a)</math>. | ||
| + | |||
| + | '''דוגמא.''' | ||
| + | נביט ב-<math>f:\mathbb{R}\rightarrow\mathbb{R}</math> המוגדרת על ידי <math>f(x)=x^2</math> ואינה חח"ע. נכון לומר שהפונקציה המצומצמת <math>f|_{\mathbb{N}}</math> כן חח"ע. | ||
| + | |||
| + | |||
| + | '''תרגיל.''' | ||
| + | תהי <math>f:X\rightarrow Y</math> פונקציה, הוכח שקיימת קבוצה A כך ש-<math>f|_A</math> חח"ע עם אותה התמונה כמו הפונקציה המקורית (כלומר <math>im(f|_A)=im(f)</math>). | ||
| + | |||
| + | '''פתרון.''' | ||
| + | |||
| + | נגדיר לכל <math>y\in im(f)</math> את הקבוצה של המקורות שלו <math>B_y:=f^{-1}(\{y\})</math> | ||
| + | כעת נבחר מכל <math>B_y</math> איבר יחיד <math>x_y\in B_y</math>. נגדיר <math>A=\{x_y | y\in im (f)\}</math>. כיוון שבחרנו מקור '''לכל''' תמונה, ובחרנו מקור '''אחד''' אזי <math>f|_A</math> חח"ע עם אותו טווח של <math>f</math>. | ||
| + | |||
| + | '''אזהרה!''' ההוכחה מתבססת על אקסיומת הבחירה (נפגש איתה בהמשך) | ||
| + | ==== תרגיל ==== | ||
| + | תהיינה <math>f:A\to B, g:B\to C</math> פונקציות כך ש <math>g\circ f</math> חח"ע. הוכיחו כי <math>g|_{Im(f)}</math> חח"ע. | ||
| + | |||
| + | הוכחה: אם נצמצם את הטווח והתחום של הפונקציות, <math>f':A\to Im(f), g|_{Im(f)}:Im(f)\to C</math>, נקבל כי <math>g\circ f=g|_{Im(f)}\circ f'</math> חח"ע ובנוסף <math>f'</math> חח"ע ועל. מכאן ש <math>g|_{Im(f)}=g\circ f\circ f'^{-1}</math> חח"ע כהרכבה של חח"ע. | ||
גרסה אחרונה מ־14:49, 27 ביולי 2021
תוכן עניינים
המשך פונקציות - פונקציות על תת-קבוצות
תמונות חלקיות
הגדרה. תהי  פונקציה, ויהיו תת קבוצות
פונקציה, ויהיו תת קבוצות 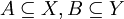 . אזי התמונה החלקית של A תחת f היא התת-קבוצה
. אזי התמונה החלקית של A תחת f היא התת-קבוצה 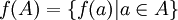 , והתמונה החלקית ההפוכה של B תחת f היא התת-קבוצה
, והתמונה החלקית ההפוכה של B תחת f היא התת-קבוצה 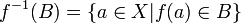 .
.
שימו לב להבדל בין התמונה ההפוכה 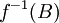 לבין הפונקציה ההופכית
לבין הפונקציה ההופכית 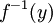 . התמונה ההפוכה איננה מניחה כי הפונקציה f הפיכה. הדרך להבחין בין פונקציה הפיכה לתמונה ההפוכה היא לבדוק האם בין הסוגריים נמצא איבר של התמונה (בדוגמאות לעיל זהו
. התמונה ההפוכה איננה מניחה כי הפונקציה f הפיכה. הדרך להבחין בין פונקציה הפיכה לתמונה ההפוכה היא לבדוק האם בין הסוגריים נמצא איבר של התמונה (בדוגמאות לעיל זהו 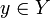 ) או שנמצאת תת-קבוצה של התמונה (בדוגמאות לעיל זו
) או שנמצאת תת-קבוצה של התמונה (בדוגמאות לעיל זו 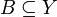 ).
).
דוגמאות
תהא 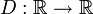 פונקצית דריכלה. אזי
פונקצית דריכלה. אזי 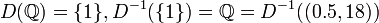
תהא 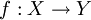 פונקצית . אזי
פונקצית . אזי 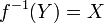
תהא 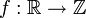 פונקצית הערך השלם התחתון. אזי
פונקצית הערך השלם התחתון. אזי 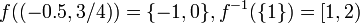
תכונות
- אם
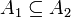 אזי
אזי 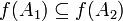
- אם
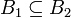 אזי
אזי 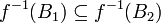
- הוכיחו/הפריכו טענות מקבילות עם משלים של קבוצות.
תרגיל
הוכיחו/הפריכו: תהי f פונקציה 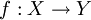 ותהיינה
ותהיינה 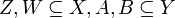 . אזי
. אזי
פתרון: תחשבו. עדיף את שני האחרונים, כי הראשונים לפעמים נעשים בהרצאה.
תרגיל
הוכח/הפרך: תהיינה 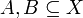 ותהי f פונקציה
ותהי f פונקציה 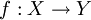 . אזי
. אזי 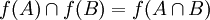
פתרון.
נפריך על ידי דוגמא נגדית. נניח וf אינה חח"ע, כלומר קיימים 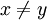 כך ש
כך ש 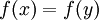 . ניקח
. ניקח 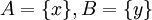 אזי:
אזי:
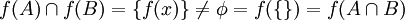
הערה תמיד מתקיים 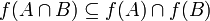
הערה הטענה נכונה אם  חח"ע. הוכיחו!
חח"ע. הוכיחו!
תרגיל (בהרצאה בד"כ)
תהי  ותהי
ותהי 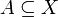 . הוכח
. הוכח 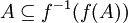 . וקיים שיוויון אם
. וקיים שיוויון אם  חח"ע
חח"ע
פתרון.
יהא 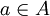 אזי
אזי 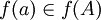 ולכן
ולכן 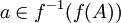 .
.
נראה את ההכלה בכיוון השני אם  חח"ע:
חח"ע:
יהא 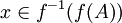 לכן
לכן 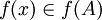 לכן
לכן 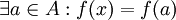 . כיוון ש
. כיוון ש  חח"ע נובע כי
חח"ע נובע כי 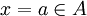
דוגמא שלא מתקיים שיוויון 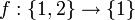 (יש דרך אחת להגדיר את הפונקציה). אזי נגדיר
(יש דרך אחת להגדיר את הפונקציה). אזי נגדיר 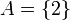 ומתקיים
ומתקיים 
תרגיל (בXI)
תהי  ותהי
ותהי 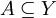 . הוכח
. הוכח 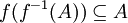 . וקיים שיוויון אם
. וקיים שיוויון אם  על
על
פתרון.
יהא 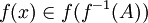 כאשר
כאשר 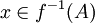 ולכן
ולכן  .
.
נראה את ההכלה בכיוון השני אם  על:
על:
יהא 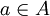 כיוון ש f על
כיוון ש f על 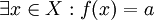 לכן
לכן 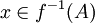 . ואז
. ואז 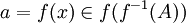
דוגמא שלא מתקיים שיוויון 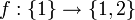 המוגדרת
המוגדרת 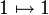 . אזי נגדיר
. אזי נגדיר 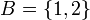 ומתקיים
ומתקיים 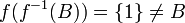 .
.
תרגיל ממבחן (קצת משודרג)
יהיו 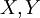 שתי קבוצות, ותהי
שתי קבוצות, ותהי  פונקציה כלשהי. נגדיר את הפונקציה
פונקציה כלשהי. נגדיר את הפונקציה 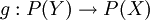 על ידי
על ידי 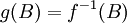 .
בדוק את הקשר בין החח"ע/על של f לבין אלה של g. (כלומר, מה גורר את מה בהכרח).
.
בדוק את הקשר בין החח"ע/על של f לבין אלה של g. (כלומר, מה גורר את מה בהכרח).
פתרון.
1. נמצא ב XI הטענה f על אמ"מ g חח"ע
בכיוון אחד- נתון ש f על. נניח 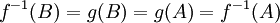 נפעיל את f על שני הצדדים ונקבל (בגלל ש f על)
נפעיל את f על שני הצדדים ונקבל (בגלל ש f על) 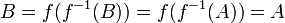
בכיוון השני- נתון כי g חח"ע. נניח בשלילה כי f אינה על אזי 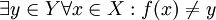 לכן
לכן 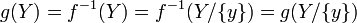 בסתירה לחח"ע של g.
בסתירה לחח"ע של g.
2. f חח"ע אמ"מ g על
בכיוון אחד- נתון f חח"ע. אזי 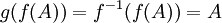 ולכן g על ( עבור A המקור שלה יהיה
ולכן g על ( עבור A המקור שלה יהיה 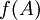 )
)
בכיוון השני- נתון g על. נניח בשלילה ש f אינה חח"ע אזי קיימים 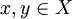 שונים כך ש
שונים כך ש 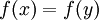 . נביט בנקודון
. נביט בנקודון 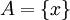
כיוון ש g על קיימת 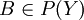 כך ש
כך ש 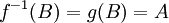
לכן 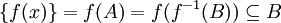
ולכן 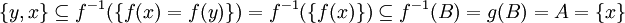
לכן 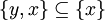 כלומר
כלומר  . סתירה.
. סתירה.
מכאן ניתן להסיק כי שאר הגרירות אינן מוכרחות:
- ייתכן ו-f חח"ע אך g אינה כזו (ניקח f חח"ע שאינה על אזי g אינה חח"ע לפי 1)
- יתכן ו-g חח"ע אך f אינה כזו. (ניקח g חח"ע שאינה על אזי f אינה חח"ע לפי 2)
- ייתכן ו-f על אך g אינה כזו (ניקח f על שאינה חח"ע אזי g אינה על לפי 2)
- ייתכן ו-g על אך f אינה כזו (ניקח g על שאינה חח"ע אזי f אינה על לפי 1)
אתם מוזמנים לתת דוגמאות למסקנות לעיל
למשל:
יהיו 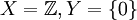 . אזי קיימת פונקציה f יחידה מX לY. פונקציה זו אינה חח"ע כמובן, אך g כן חח"ע שכן
. אזי קיימת פונקציה f יחידה מX לY. פונקציה זו אינה חח"ע כמובן, אך g כן חח"ע שכן 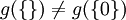 ואלה הקבוצות היחידות בקבוצת החזקה של Y.
ואלה הקבוצות היחידות בקבוצת החזקה של Y.
תרגיל (בהרצאה בד"כ)
תהיינה A,B קבוצות לא ריקות. הוכיחו כי:
- אם קיימת
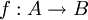 חח"ע אזי קיימת
חח"ע אזי קיימת 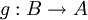 על.
על. - אם A,B סופיות: קיימת
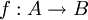 חח"ע אמ"מ
חח"ע אמ"מ 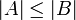
- אם A,B סופיות: קיימת
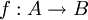 על אמ"מ
על אמ"מ 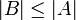
פונקציות המכבדות יחס שקילות
הגדרה. תהי 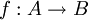 , ויהי R יחס שקילויות על A. אומרים כי f מוגדרת היטב על
, ויהי R יחס שקילויות על A. אומרים כי f מוגדרת היטב על 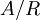 אם
אם 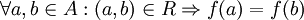
כלומר אם a שקול ל b אזי 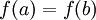 .
.
למה זה טוב?
כדי שנוכל להגדיר פונקציה על קבוצת המנה 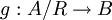 ע"י
ע"י ![[a]_R \mapsto f(a)](/images/math/a/5/6/a56f87e88ee31931dfa2d032aa2697af.png)
באופן מפורש ![g=\{([a],f(a))|a\in A\}](/images/math/8/6/e/86e85e73a964258f5be37814ee1b6ecb.png) .
.
טענה: g אכן פונקציה
הוכחה:
1. g שלמה - "לפי העיניים". כלל ההתאמה מנוסח כך שהיחס הוא שלם.
2. g חד ערכית- נניח ![[a]=[b]](/images/math/5/9/c/59cf3abe8a280a0de4a9dd1cfa304603.png) , צ"ל
, צ"ל ![g([a])=g([b])](/images/math/c/3/9/c39fed416ad833091eb1647bea772e0f.png) . מהנתון ש
. מהנתון ש ![[a]=[b]](/images/math/5/9/c/59cf3abe8a280a0de4a9dd1cfa304603.png) נובע ש
נובע ש 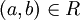 , ולכן, לפי הגדרת f כמוגדרת היטב על קבוצת המנה, מתקיים
, ולכן, לפי הגדרת f כמוגדרת היטב על קבוצת המנה, מתקיים 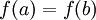 , ולפי הגדרת g מתקיים
, ולפי הגדרת g מתקיים ![g([a])=f(a)=f(b)=g([b])](/images/math/b/b/4/bb463262f1bfb8fc639c78ad363d5eb5.png) .
.
דוגמא
נגדיר על השלמים יחס שקילות ע"י x~y אמ"מ y=x or y=-x.
בדקו מי מהבאות היא פונקציה מקבוצת המנה לשלמים:
דוגמא
האם f על הרציונאליים המוגדרת על ידי 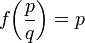 מוגדרת היטב?
מוגדרת היטב?
פתרון
לא! כזכור הרציונאליים הם קבוצת מנה של 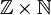 . לפי היחס שהגדרנו מתקיים
. לפי היחס שהגדרנו מתקיים  אבל לא מתקיים
אבל לא מתקיים 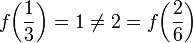
במילים: לא ברור לאן f שולחת את השבר שליש!
הערה: בכוונה ניסחנו את התרגיל באופן הרומז על יחס השקילויות מבלי לומר אותו במפורש. זו הדרך בה נתקל במושג 'מוגדר היטב' במהלך התואר - יחס השקילויות יהיה מרומז בלבד.
פונקציה מצומצמת
הגדרה.
תהי  ותהי
ותהי 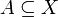 . הפונקציה f מצומצמת לA מוגדרת על ידי:
. הפונקציה f מצומצמת לA מוגדרת על ידי:  כך ש-
כך ש-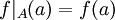 .
.
דוגמא.
נביט ב-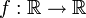 המוגדרת על ידי
המוגדרת על ידי 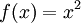 ואינה חח"ע. נכון לומר שהפונקציה המצומצמת
ואינה חח"ע. נכון לומר שהפונקציה המצומצמת 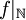 כן חח"ע.
כן חח"ע.
תרגיל.
תהי  פונקציה, הוכח שקיימת קבוצה A כך ש-
פונקציה, הוכח שקיימת קבוצה A כך ש-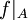 חח"ע עם אותה התמונה כמו הפונקציה המקורית (כלומר
חח"ע עם אותה התמונה כמו הפונקציה המקורית (כלומר 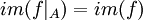 ).
).
פתרון.
נגדיר לכל 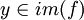 את הקבוצה של המקורות שלו
את הקבוצה של המקורות שלו 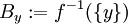 כעת נבחר מכל
כעת נבחר מכל 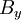 איבר יחיד
איבר יחיד 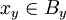 . נגדיר
. נגדיר 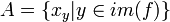 . כיוון שבחרנו מקור לכל תמונה, ובחרנו מקור אחד אזי
. כיוון שבחרנו מקור לכל תמונה, ובחרנו מקור אחד אזי 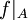 חח"ע עם אותו טווח של
חח"ע עם אותו טווח של  .
.
אזהרה! ההוכחה מתבססת על אקסיומת הבחירה (נפגש איתה בהמשך)
תרגיל
תהיינה 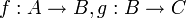 פונקציות כך ש
פונקציות כך ש 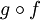 חח"ע. הוכיחו כי
חח"ע. הוכיחו כי 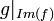 חח"ע.
חח"ע.
הוכחה: אם נצמצם את הטווח והתחום של הפונקציות, 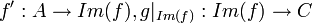 , נקבל כי
, נקבל כי 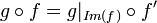 חח"ע ובנוסף
חח"ע ובנוסף 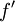 חח"ע ועל. מכאן ש
חח"ע ועל. מכאן ש 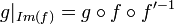 חח"ע כהרכבה של חח"ע.
חח"ע כהרכבה של חח"ע.
![f^{-1}[A]\cap f^{-1}[B]=f^{-1}[A\cap B]](/images/math/e/0/1/e01dc064c1cc99acbeb007edc2493b46.png)
![f^{-1}[A]\cup f^{-1}[B]=f^{-1}[A\cup B]](/images/math/b/b/9/bb9ed0e5facbd459ae1ac44ac858a16a.png)
![f^{-1}[A\setminus B]=f^{-1}[A]\setminus f^{-1}[B]](/images/math/5/d/3/5d3835b5abae64fe45b097b0040df0df.png)
![f^{-1}[A]\triangle f^{-1}[B]=f^{-1}[A\triangle B]](/images/math/0/4/c/04c257813339560d0e1f43247516cd84.png)
![f[Z]\triangle f[W]=f[Z\triangle W]](/images/math/9/3/3/93363850925022efced359d7360eb0c8.png)
![\{([n]_{~},n): n\in \mathbb{Z} \}](/images/math/5/9/3/5939401560cf4438276d4d246015abb1.png)
![\{([n]_{~},n^2): n\in \mathbb{Z} \}](/images/math/1/b/3/1b3885390b6a94b88b65977d6bd69be1.png)