88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 5
המשך פונקציות
הגדרה. תהי  פונקציה, ויהיו תת קבוצות
פונקציה, ויהיו תת קבוצות 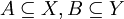 . אזי
. אזי 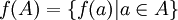 ,
, 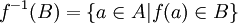 .
.
שימו לב שהסימון 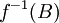 אינו רומז בשום צורה שהפונקציה צריכה להיות הפיכה, הגדרה זו תקפה לכל פונקציה.
אינו רומז בשום צורה שהפונקציה צריכה להיות הפיכה, הגדרה זו תקפה לכל פונקציה.
תרגיל.
הוכח/הפרך: תהא 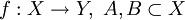 אזי
אזי 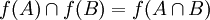
פתרון.
נניח וf אינה חח"ע, כלומר קיימים 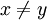 כך ש
כך ש 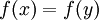 . ניקח
. ניקח 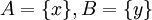 אזי:
אזי:
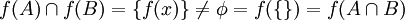
תרגיל.
תהי  חח"ע, ותהי
חח"ע, ותהי 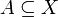 . הוכח
. הוכח 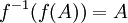 .
.
פתרון.
ישירות מההגדרות נובע שאם 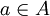 אזי
אזי 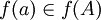 ולכן
ולכן 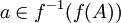 . סה"כ הראנו
. סה"כ הראנו 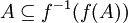 . (עד כה זה נכון לכל העתקה, לאו דווקא חח"ע.)
. (עד כה זה נכון לכל העתקה, לאו דווקא חח"ע.)
נניח כעת בשלילה ש 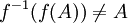 לכן קיים
לכן קיים 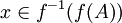 כך ש
כך ש 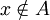 . לכן לפי ההגדרה,
. לכן לפי ההגדרה, 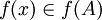 . לכן קיים a בA כך ש
. לכן קיים a בA כך ש 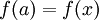 . מתוך החח"ע נובע ש-x=a בסתירה.
. מתוך החח"ע נובע ש-x=a בסתירה.
תרגיל ממבחן (קצת משודרג).
יהיו 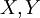 שתי קבוצות, ותהי
שתי קבוצות, ותהי  פונקציה כלשהי. נגדיר את הפונקציה
פונקציה כלשהי. נגדיר את הפונקציה 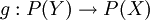 על ידי
על ידי 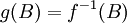 .
בדוק את הקשר בין החח"ע/על של f לבין אלה של g. (כלומר, מה גורר את מה בהכרח).
.
בדוק את הקשר בין החח"ע/על של f לבין אלה של g. (כלומר, מה גורר את מה בהכרח).
פתרון.
תהי f חח"ע שאינה על (קל למצוא כאלה). אזי 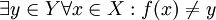 . לכן
. לכן 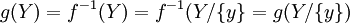 בסתירה לחח"ע של g.
בסתירה לחח"ע של g.
- לכן ייתכן ו-f חח"ע אך g אינה כזו.
תהי f כך ש-g חח"ע. כפי שראינו לעיל, ניתן ישר להסיק ש-f הינה על.
נוכיח שאם f על אזי g חח"ע; נניח בשלילה שg אינה חח"ע, אזי קיימות שתי קבוצות 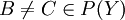 כך ש
כך ש 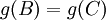 . בלי הגבלת הכלליות, נניח שקיים איבר
. בלי הגבלת הכלליות, נניח שקיים איבר 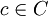 כך ש
כך ש 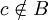 . מכיוון ש-f על, קיים איבר a כך ש
. מכיוון ש-f על, קיים איבר a כך ש 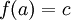 , לכן
, לכן 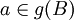 , ואז קיים
, ואז קיים 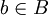 כך ש
כך ש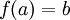 ולכן b=c בסתירה.
ולכן b=c בסתירה.
- אם כן, הוכחנו ש-f על אם"ם g חח"ע.
יהיו 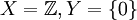 . אזי קיימת פונקציה f יחידה מX לY. פונקציה זו אינה חח"ע כמובן, אך g כן חח"ע שכן
. אזי קיימת פונקציה f יחידה מX לY. פונקציה זו אינה חח"ע כמובן, אך g כן חח"ע שכן 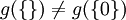 ואלה הקבוצות היחידות בקבוצת החזקה של Y.
ואלה הקבוצות היחידות בקבוצת החזקה של Y.
- לכן יתכן ו-g חח"ע אך f אינה כזו.
נניח וg על ונניח בשלילה ש-f אינה חח"ע. לכן קיימים 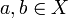 שונים כך ש
שונים כך ש 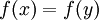 . נביט בנקודון
. נביט בנקודון 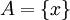 נניח וקיימת
נניח וקיימת 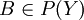 כך ש
כך ש 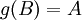 , לכן
, לכן 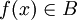 . אבל אז בעצם גם
. אבל אז בעצם גם 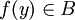 ולכן
ולכן 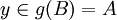 בסתירה. לכן f חח"ע.
בסתירה. לכן f חח"ע.
נניח f חח"ע, הוכחנו כבר שבהכרח 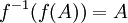 לכל A תת קבוצה של X. נובע ש
לכל A תת קבוצה של X. נובע ש 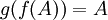 ולכן g הינה על.
ולכן g הינה על.
- סה"כ, הוכחנו שf חח"ע אם"ם g הינה על.
ניקח f פונקציה חח"ע שאינה על, לכן g היא על.
- לכן ייתכן ו-g הינה על אך f אינה על
באופן דומה ניקח f על שאינה חח"ע, לכן g אינה על.
- לכן ייתכן ו-f הינה על אך g אינה על
הגדרה.
תהי  ותהי
ותהי 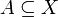 . הפונקציה f מצומצמת לA מוגדרת על ידי:
. הפונקציה f מצומצמת לA מוגדרת על ידי:  כך ש
כך ש 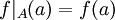 .
.
דוגמא.
נביט ב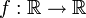 המוגדרת על ידי
המוגדרת על ידי 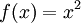 ואינה חח"ע. נכון לומר שהפונקציה המצומצמת
ואינה חח"ע. נכון לומר שהפונקציה המצומצמת 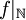 כן חח"ע.
כן חח"ע.
תרגיל.
תהי  פונקציה, הוכח שקיימת קבוצה A כך ש
פונקציה, הוכח שקיימת קבוצה A כך ש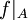 חח"ע
חח"ע
פתרון.
פייי זו שאלה קשה. תזכירו לנו אותה כאשר נגיע לאקסיומת הבחירה. (שכן נביט ב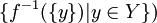 ונרצה לבחור איבר יחיד מבין כל קבוצה כזו. אקסיומת הבחירה היא זו המאפשרת לנו לבצע בחירה זו בשלום.)
ונרצה לבחור איבר יחיד מבין כל קבוצה כזו. אקסיומת הבחירה היא זו המאפשרת לנו לבצע בחירה זו בשלום.)
הגדרה. תהי 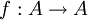 , ויהי R יחס שקילויות על A. אומרים כי f מוגדרת היטב על
, ויהי R יחס שקילויות על A. אומרים כי f מוגדרת היטב על 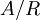 אם
אם 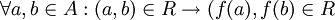
תרגיל מוטיבציה להגדרה לעיל.
המוטיבציה להגדרה הזו היא היכולת לגזור ממנה פונקציה על חבורת המנה. נגדיר יחס על חבורת המנה ![g=\{([a],[f(a)])|a\in A\}](/images/math/3/a/f/3af13d48c202bd1a70c19af62d07aad7.png) . נוכיח ש-g הינה חד-ערכית ולכן פונקציה.
. נוכיח ש-g הינה חד-ערכית ולכן פונקציה.
הוכחה
נניח וקיימים 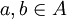 כך ש
כך ש ![[a]=[b]](/images/math/5/9/c/59cf3abe8a280a0de4a9dd1cfa304603.png) . לכן
. לכן 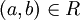 ולכן
ולכן 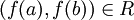 ולכן
ולכן ![[f(a)]=[f(b)]](/images/math/7/b/6/7b6043fa874b5980c7368d74a90d27c6.png) . לכן לא ייתכן מצב בו
. לכן לא ייתכן מצב בו 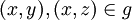 אבל
אבל 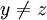 .
.
דוגמא.
האם הפונקציה f על הרציונאליים המוגדרת על ידי 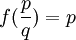 מוגדרת היטב?
מוגדרת היטב?
פתרון.
יש לשים לב שלא באמת הגדרנו את הפונקציה על הרציונאליים, אלא על אוסף הזוגות הסדורים של שלמים 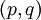 כך שהאיבר הימני שונה מאפס. נגדיר על קבוצה זו את יחס השקילויות R המוגדר על ידי
כך שהאיבר הימני שונה מאפס. נגדיר על קבוצה זו את יחס השקילויות R המוגדר על ידי 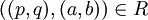 אם
אם 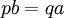 . נראה כי f אינה מוגדרת היטב בתנאים אלו:
. נראה כי f אינה מוגדרת היטב בתנאים אלו:
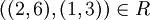 אולם
אולם 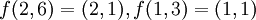 ו
ו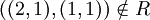 .
.
בכוונה ניסחנו את התרגיל באופן הרומז על יחס השקילויות מבלי לומר אותו במפורש. זו הדרך בה נתקל במושג 'מוגדר היטב' במהלך התואר - יחס השקילויות יהיה מרומז בלבד.