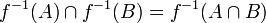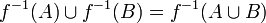88-195 בדידה לתיכוניסטים תשעא/מערך שיעור/שיעור 5
תוכן עניינים
המשך פונקציות - פונקציות על תת-קבוצות
תמונות חלקיות
הגדרה. תהי  פונקציה, ויהיו תת קבוצות
פונקציה, ויהיו תת קבוצות 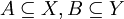 . אזי התמונה החלקית של A תחת f היא התת-קבוצה
. אזי התמונה החלקית של A תחת f היא התת-קבוצה 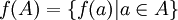 , והתמונה החלקית ההפוכה של B תחת f היא התת-קבוצה
, והתמונה החלקית ההפוכה של B תחת f היא התת-קבוצה 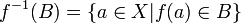 .
.
שימו לב להבדל בין התמונה ההפוכה 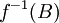 לבין הפונקציה ההופכית
לבין הפונקציה ההופכית 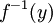 . התמונה ההפוכה איננה מניחה כי הפונקציה f הפיכה. הדרך להבחין בין פונקציה הפיכה לתמונה ההפוכה היא לבדוק האם בין הסוגריים נמצא איבר של התמונה (בדוגמאות לעיל זהו
. התמונה ההפוכה איננה מניחה כי הפונקציה f הפיכה. הדרך להבחין בין פונקציה הפיכה לתמונה ההפוכה היא לבדוק האם בין הסוגריים נמצא איבר של התמונה (בדוגמאות לעיל זהו 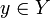 ) או שנמצאת תת-קבוצה של התמונה (בדוגמאות לעיל זו
) או שנמצאת תת-קבוצה של התמונה (בדוגמאות לעיל זו 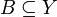 ).
).
דוגמאות
תהא 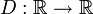 פונקצית דריכלה. אזי
פונקצית דריכלה. אזי 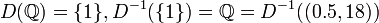
תהא 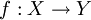 פונקצית . אזי
פונקצית . אזי 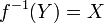
תהא 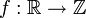 פונקצית הערך השלם התחתון. אזי
פונקצית הערך השלם התחתון. אזי 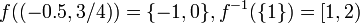
תכונות
- אם
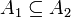 אזי
אזי 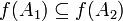
- אם
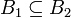 אזי
אזי 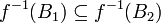
- הוכיחו/הפריכו טענות מקבילות עם משלים של קבוצות.
תרגיל
הוכיחו/הפריכו: תהי f פונקציה 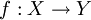 ותהיינה
ותהיינה 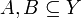 . אזי
. אזי
פתרון: תחשבו
תרגיל
הוכח/הפרך: תהיינה 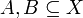 ותהי f פונקציה
ותהי f פונקציה 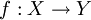 . אזי
. אזי 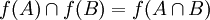
פתרון.
נפריך על ידי דוגמא נגדית. נניח וf אינה חח"ע, כלומר קיימים 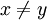 כך ש
כך ש 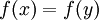 . ניקח
. ניקח 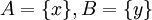 אזי:
אזי:
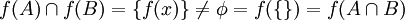
הערה תמיד מתקיים 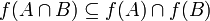
הערה הטענה נכונה אם  חח"ע. הוכיחו!
חח"ע. הוכיחו!
תרגיל
תהי  ותהי
ותהי 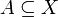 . הוכח
. הוכח 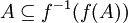 . וקיים שיוויון אם
. וקיים שיוויון אם  חח"ע
חח"ע
פתרון.
יהא 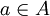 אזי
אזי 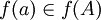 ולכן
ולכן 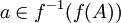 .
.
נראה את ההכלה בכיוון השני אם  חח"ע:
חח"ע:
יהא 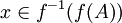 לכן
לכן 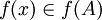 לכן
לכן 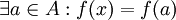 . כיוון ש
. כיוון ש  חח"ע נובע כי
חח"ע נובע כי 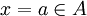
דוגמא שלא מתקיים שיוויון 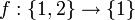 (יש דרך אחת להגדיר את הפונקציה). אזי נגדיר
(יש דרך אחת להגדיר את הפונקציה). אזי נגדיר 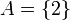 ומתקיים
ומתקיים 
תרגיל
תהי  ותהי
ותהי 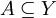 . הוכח
. הוכח 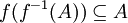 . וקיים שיוויון אם
. וקיים שיוויון אם  על
על
פתרון.
יהא 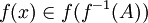 כאשר
כאשר 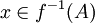 ולכן
ולכן  .
.
נראה את ההכלה בכיוון השני אם  על:
על:
יהא 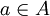 כיוון ש f על
כיוון ש f על 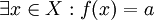 לכן
לכן 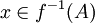 . ואז
. ואז 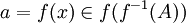
דוגמא שלא מתקיים שיוויון 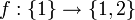 המוגדרת
המוגדרת 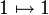 . אזי נגדיר
. אזי נגדיר 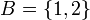 ומתקיים
ומתקיים 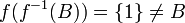 .
.
תרגיל ממבחן (קצת משודרג)
יהיו 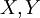 שתי קבוצות, ותהי
שתי קבוצות, ותהי  פונקציה כלשהי. נגדיר את הפונקציה
פונקציה כלשהי. נגדיר את הפונקציה 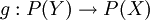 על ידי
על ידי 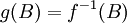 .
בדוק את הקשר בין החח"ע/על של f לבין אלה של g. (כלומר, מה גורר את מה בהכרח).
.
בדוק את הקשר בין החח"ע/על של f לבין אלה של g. (כלומר, מה גורר את מה בהכרח).
פתרון.
1. f על אמ"מ g חח"ע
בכיוון אחד- נתון ש f על. נניח 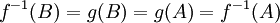 נפעיל את f על שני הצדדים ונקבל (בגלל ש f על)
נפעיל את f על שני הצדדים ונקבל (בגלל ש f על) 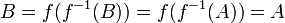
בכיוון השני- נתון כי g חח"ע. נניח בשלילה כי f אינה על אזי 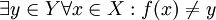 לכן
לכן 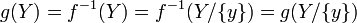 בסתירה לחח"ע של g.
בסתירה לחח"ע של g.
2. f חח"ע אמ"מ g על
בכיוון אחד- נתון f חח"ע. אזי 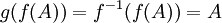 ולכן g על ( עבור A המקור שלה יהיה
ולכן g על ( עבור A המקור שלה יהיה 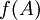 )
)
בכיוון השני- נתון g על. נניח בשלילה ש f אינה חח"ע אזי קיימים 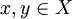 שונים כך ש
שונים כך ש 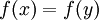 . נביט בנקודון
. נביט בנקודון 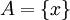
כיוון ש g על קיימת 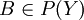 כך ש
כך ש 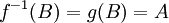
לכן 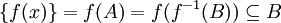
ולכן 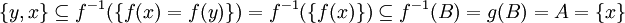
לכן 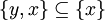 כלומר
כלומר  . סתירה.
. סתירה.
מכאן ניתן להסיק כי שאר הגרירות אינן מוכרחות:
- ייתכן ו-f חח"ע אך g אינה כזו (ניקח f חח"ע שאינה על אזי g אינה חח"ע לפי 1)
- יתכן ו-g חח"ע אך f אינה כזו. (ניקח g חח"ע שאינה על אזי f אינה חח"ע לפי 2)
- ייתכן ו-f על אך g אינה כזו (ניקח f על שאינה חח"ע אזי g אינה על לפי 2)
- ייתכן ו-g על אך f אינה כזו (ניקח g על שאינה חח"ע אזי f אינה על לפי 1)
אתם מוזמנים לתת דוגמאות למסקנות לעיל
למשל:
יהיו 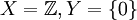 . אזי קיימת פונקציה f יחידה מX לY. פונקציה זו אינה חח"ע כמובן, אך g כן חח"ע שכן
. אזי קיימת פונקציה f יחידה מX לY. פונקציה זו אינה חח"ע כמובן, אך g כן חח"ע שכן 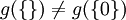 ואלה הקבוצות היחידות בקבוצת החזקה של Y.
ואלה הקבוצות היחידות בקבוצת החזקה של Y.
תרגיל
תהא 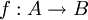 פונקציה בין קבוצות לא ריקות. הוכיחו כי
פונקציה בין קבוצות לא ריקות. הוכיחו כי
- אם f חח"ע אזי קיימת
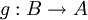 על.
על. - במידה ו A,B סופיות: f חח"ע אמ"מ
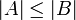
- במידה ו A,B סופיות: f על אמ"מ
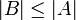
פונקציה מצומצמת
הגדרה.
תהי  ותהי
ותהי 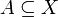 . הפונקציה f מצומצמת לA מוגדרת על ידי:
. הפונקציה f מצומצמת לA מוגדרת על ידי:  כך ש-
כך ש-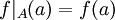 .
.
דוגמא.
נביט ב-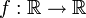 המוגדרת על ידי
המוגדרת על ידי 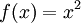 ואינה חח"ע. נכון לומר שהפונקציה המצומצמת
ואינה חח"ע. נכון לומר שהפונקציה המצומצמת 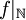 כן חח"ע.
כן חח"ע.
תרגיל.
תהי  פונקציה, הוכח שקיימת קבוצה A כך ש-
פונקציה, הוכח שקיימת קבוצה A כך ש-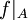 חח"ע עם אותה התמונה כמו הפונקציה המקורית (כלומר
חח"ע עם אותה התמונה כמו הפונקציה המקורית (כלומר 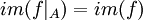 ).
).
פתרון.
נגדיר לכל 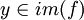 את הקבוצה של המקורות שלו
את הקבוצה של המקורות שלו 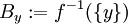 כעת נבחר מכל
כעת נבחר מכל 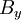 איבר יחיד
איבר יחיד 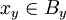 . נגדיר
. נגדיר 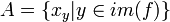 . כיוון שבחרנו מקור לכל תמונה, ובחרנו מקור אחד אזי
. כיוון שבחרנו מקור לכל תמונה, ובחרנו מקור אחד אזי 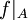 חח"ע עם אותו טווח של
חח"ע עם אותו טווח של  .
.
אזהרה! ההוכחה מתבססת על אקסיומת הבחירה (נפגש איתה בהמשך)