88-212 תשעב סמסטר ב/תקצירי הרצאות

תקצירי הרצאות

הרצאה ראשונה

כוכב הקורס הוא המבנה האלגברי הקרוי חוג (ובשמו המלא, "חוג עם יחידה"). בתפקיד אורח - חוג בלי יחידה, שהוא מבנה עם חיבור וכפל, המקיים את כל האקסיומות של החוג, למעט אולי קיומו של איבר יחידה (ולכן חוג בלי יחידה, שיש לו איבר יחידה, נקרא חוג; המלים "בלי יחידה" הן חלק מהשם ולא תאור תכונה עובדתי).

בחוג בלי יחידה יכולים להיות יחידות מימין ומשמאל. אם באותו חוג-בלי-יחידה יש גם יחידה מימין וגם יחידה משמאל, אברים אלו שווים והם איבר יחידה במובן המלא של המלה. תת-קבוצה של חוג שהיא חוג בזכות עצמה נקראת תת-חוג. הגדרנו את המושג "תת-חוג-בלי-יחידה", המתאר את התופעה שבה חוג אחד (עם או בלי יחידה) מוכל בחוג אחר (עם או בלי יחידה), כשאין להם אותו איבר יחידה.

איבר של חוג (עם יחידה) יכול להיות הפיך מימין או משמאל. יכולים להיות לו, בהתאמה, הרבה הפיכים מימין והרבה הפיכים משמאל ("הפיך" - תכונה של האיבר עצמו; "הפכי" - תכונה של איבר אחר ביחס אליו). עם זאת, אם יש הפכי מימין ויש הפכי משמאל, אז הם שווים זה לזה, והאיבר עצמו הפיך. ההפכיים של איברים הפיכים מקיימים את התכונות המוכרות מתורת החבורות: 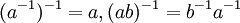$\ (a^{-1})^{-1} = a, (ab)^{-1} = b^{-1}a^{-1}$ (וביתר פירוט: אם a הפיך אז יש לו הפכי יחיד, שגם הוא הפיך, וההפכי של ההפכי הוא האיבר עצמו; כמו-כן, מכפלה של אברים הפיכים היא איבר הפיך, השווה למכפלת ההפכיים בסדר הפוך). אוסף האברים ההפיכים בחוג הוא חבורה, הנקראת חבורת ההפיכים של החוג. (ראו תרגיל 1.1.70 בחוברת לדוגמא של מכפלה xy=1 כאשר x אינו הפיך משמאל ו-y אינו הפיך מימין).

אם xy=0 (ו-x,y אינם אפס) אז x,y נקראים מחלקי אפס (שמאלי וימני בהתאמה). חוג שאין בו מחלקי אפס נקרא תחום. תחום קומוטטיבי נקרא תחום שלמות. חוג שבו כל איבר שונה מאפס הוא הפיך נקרא חוג עם חילוק. כל חוג עם חילוק הוא תחום. חוג קומוטטיבי עם חילוק נקרא שדה. כל שדה הוא תחום שלמות.

הרצאה שניה

דוגמאות ובניה של חוגים. הגדרנו מרכז של חוג (בכף קמוצה) - אוסף האברים המתחלפים עם כל האברים האחרים. כמובן, המרכז של חוג הוא תת-חוג קומוטטיבי שלו, והמרכז שווה לכל החוג אם ורק אם החוג עצמו קומוטטיבי. ראו גם הגדרה 1.1.46 עבור המרכז (כף סגולה).

בנינו חוג מטריצות בגודל קבוע מעל חוג נתון (חוג המטריצות לעולם אינו תחום, פרט למקרה הטריוויאלי של מטריצות בגודל 1x1). המרכז של חוג המטריצות מעל R שווה לאוסף המטריצות הסקלריות שמקדמיהן שייכים למרכז של R.

בנינו חוג פולינומים מעל חוג נתון. אם R הוא תחום, גם חוג הפולינומים מעליו הוא תחום (בזכות פונקציית המעלה). המרכז של חוג הפולינומים מעל R שווה לאוסף הפולינומים שכל מקדמיהם שייכים למרכז של R.

הגדרנו את אלגברת הקווטרניונים של המילטון, שהיא מרחב וקטורי 4-ממדי מעל הממשיים, המהווה חוג כאשר מגדירים את פעולת הכפל כראוי. החוג הזה נוצר (מעל הממשיים) על-ידי האברים i,j שהם אנטי-מתחלפים (ji=-ij) ומקיימים 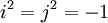$\ i^2 = j^2 = -1$ (לכן חוג זה אינו קומוטטיבי). כדי להוכיח שהוא חוג עם חילוק, הגדרנו את פונקציית הנורמה, המכלילה את הנורמה של מספרים מרוכבים. למעשה הנורמה של קווטרניון w שווה למכפלה שלו בצמוד שלו: 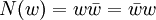$\ N(w) = w\bar{w} = \bar{w}w$. מכיוון שהנורמה של איבר שונה מאפס תמיד שונה מאפס, הצמוד חלקי הנורמה הוא ההפכי. תרגיל לא קל: נסו לחזור על הבניה הזו, המגדירה את הקווטרניונים מעל הממשיים, עם אותן תכונות של אברי הבסיס, אבל מעל למספרים המרוכבים. הוכיחו שהחוג המתקבל הוא חוג המטריצות $\ \operatorname{M}_2(\mathbb{C})$.

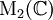הגדרנו מכפלה ישרה של חוגים (גם במקרה הסופי, וגם במקרה הכללי) כמכפלה קרטזית, עם הפעולות לפי רכיבים.

הרצאה שלישית

למדנו בניה נוספת של חוגים: בהנתן חוג R, אפשר להגדיר את חוג טורי לורן מעליו, בתור 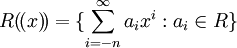$\ R(\!(x)\!) = \{\sum_{i=-n}^{\infty} a_i x^i : a_i \in R\}$ (כאן n הוא מספר שלם כלשהו, היכול כמובן להיות תלוי באיבר המדובר). את חוג טורי החזקות הפורמליים מגדירים כמעט באותו אופן: 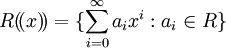$\ R(\!(x)\!) = \{\sum_{i=0}^{\infty} a_i x^i : a_i \in R\}$; השני תת-חוג של הראשון. פעולת הכפל בטורי לורן מוגדרת כפי שאפשר לצפות (והיא מוגדרת היטב בדיוק בגלל שהחישוב לכל מקדם של חזקה של x הוא סופי). חוג הפולינומים מהווה תת-חוג של חוג טורי החזקות הפורמליים. תרגיל. מיצאו את הממד של $\ F[[x]]$ כמרחב וקטורי מעל F.

כדי לטפל בטורי לורן מגדירים עליהם מעין פונקציית מעלה הפוכה, 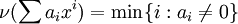$\ \nu(\sum a_i x^i) = \min \{i: a_i \neq 0\}$, הנקראת "ערך". הערך של פולינום האפס הוא מינוס אינסוף. את טורי החזקות הפורמליים אפשר לאפיין כטורי לורן שיש להם ערך חיובי. טור טיילור המוכר של 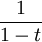$\ \frac{1}{1-t}$ מראה שכל טור חזקות פורמלי עם ערך אפס, שהמקדם המוביל שלו הוא 1, הפיך (בחוג של טורי החזקות הפורמליים).

הערך של מכפלה שווה לסכום המכפלות, וכך אפשר להוכיח כמה תכונות שימושיות: (0) טורי לורן מעל תחום מהווים תחום. (1) בחוג טורי החזקות הפורמליים, איבר הוא הפיך אם ורק אם יש לו ערך אפס והמקדם המוביל שלו הפיך בעצמו (בחוג המקדמים); (2) בחוג טורי לורן, איבר הוא הפיך אם ורק אם המקדם המוביל שלו הפיך.

בפרט, אם D חוג עם חילוק אז 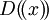$\ D(\!(x)\!)$ חוג עם חילוק; אם F שדה אז 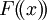$\ F(\!(x)\!)$ שדה. תרגיל: הראו שלכל איבר מערך אפס, עם מקדם מוביל 1, יש שורש ב-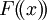$\ F(\!(x)\!)$ (הניחו שהמאפיין של F אינו 2).

(סעיף 1.2): הגדרנו אידיאלים ימניים ושמאליים, ואידיאלים דו-צדדיים (הנקראים סתם "אידיאלים"). החוג עצמו נקרא "אידיאל לא אמיתי", וכל אידיאל אחר (לרבות אידיאל האפס) הוא "אמיתי". אידיאל שמאלי אמיתי , וכל שכן אידיאל אמיתי, אינו יכול להכיל אף איבר הפיך (משמאל).

הרצאה רביעית

החיתוך של משפחת תת-חוגים הוא תת-חוג. עובדה זו מאפשרת להגדיר את "תת-החוג הנוצר (מעל לתת-חוג ידוע) על-ידי קבוצת אברים נתונה". בדומה לזה החיתוך של משפחת אידיאלים שמאליים הוא אידיאל שמאלי. החיתוך של משפחת אידיאלים הוא אידיאל.

כידוע, איחוד של שתי תת-חבורות אינו יכול להיות תת-חבורה אלא במקרה הטריוויאלי (כאשר אחת מתת-החבורות מכילה את השניה). לכן איחוד של אידיאלים כמעט תמיד אינו אידיאל. לעומת זאת, איחוד על-פני שרשרת של אידיאלים, הוא אידיאל.

סכום של אידיאלים (המוגדר כמו סכום של תת-חבורות) הוא אידיאל. (אבל סכום של תת-חוגים אינו בהכרח תת-חוג).

מכפלה של קבוצות בחוג מוגדרת כאוסף הסכומים (הסופיים כמובן) של מכפלות מן הקבוצות: 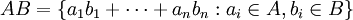$\ AB = \{a_1b_1+\cdots+a_nb_n: a_i \in A, b_i \in B\}$. מכפלה של אידיאלים היא אידיאל.

ביחס לכל אידיאל של חוג, אפשר להגדיר את חוג המנה של הקוסטים 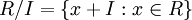$\ R/I = \{x+I: x \in R\}$. הכפל מוגדר היטב בדיוק בגלל ש-I אידיאל דו-צדדי. שאר האקסיומות נובעות בחינם מכך ש-R חוג בעצמו.

הומומורפיזם של חוגים מוגדר בדומה לחבורות, כפונקציה מחוג אחד לאחר, השומרת על כל המבנה: החיבור (ולכן גם האפס והחיסור), הכפל ואיבר היחידה. שיכון הוא הומומורפיזם חד-חד-ערכי. איזומורפיזם הוא הומומורפיזם חד-חד-ערכי ועל (ולכן שיכון הוא איזומורפיזם של חוג אחד עם תת-חוג של חוג אחר). מתקיימים משפטי האיזומורפיזמים: (1) לכל הומומורפיזם 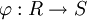$\ \varphi : R \rightarrow S$ מתקיים 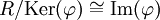$\ R/\operatorname{Ker}(\varphi) \cong \operatorname{Im}(\varphi)$. (2) לכל אידיאל I של חוג R, ולכל תת-חוג S של R, 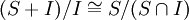$\ (S+I)/I \cong S/(S \cap I)$. (3) לכל שני אידיאלים I,J של חוג R כך ש- 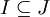$\ I \subseteq J$, חוגי המנה מקיימים $\ (R/I)/(J/I) \cong R/J$.

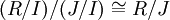לסיכום משפטים אלה, מתקיים משפט ההתאמה בין אידיאלים של החוג R המכילים אידיאל קבוע I, לבין אידיאלים של חוג המנה R/I. ההתאמה שומרת על כל דבר שאפשר להעלות על הדעת: הכלה, חיבור, כפל, חיתוך ומנות.

הרצאה חמישית

הוכחנו בעזרת הלמה של צורן שבכל חוג עם יחידה, כל אידיאל מוכל באידיאל מקסימלי; בפרט יש בחוג אידיאלים מקסימליים. הגדרנו חוג פשוט (שהוא חוג ללא אידיאלים אמיתיים חוץ מאפס), וראינו שאידיאל הוא מקסימלי אם ורק אם המנה ביחס אליו פשוטה. החוגים הפשוטים הקומוטטיביים אינם אלא שדות, ולכן אידיאל בחוג קומוטטיבי הוא מקסימלי אם ורק אם המנה ביחס אליו היא שדה. למעשה, המרכז של כל חוג פשוט הוא שדה.

חוג עם חילוק הוא חוג ללא אידיאלים חד-צדדיים (אמיתיים שונים מאפס), ולכן כל חוג עם חילוק הוא פשוט. כל חוג מטריצות מעל חוג פשוט הוא פשוט (עובדה זו, שלא הוכחנו, נובעת מכך שכל אידיאל בחוג מטריצות הוא למעשה אוסף המטריצות מעל אידיאל מתאים בחוג המקדמים).

חוג ראשוני הוא חוג שבו מכפלת אידיאלים שונים מאפס אינה אפס. כל תחום הוא ראשוני, ובחוגים קומוטטיביים אין הבדל: חוג קומוטטיבי הוא ראשוני אם ורק אם אין בו מחלקי אפס. כל חוג פשוט הוא ראשוני, אבל משפחת החוגים הראשוניים רחבה בהרבה. למשל, חוג שיש לו הרחבה מרכזית שהיא חוג פשוט, הוא ראשוני. מכאן ש-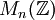$\ M_n(\mathbb{Z})$ הוא חוג ראשוני, שאינו פשוט ואינו תחום.

הרצאה שישית

הגדרנו מהו אידיאל ראשוני (אם הוא "מחלק" מכפלה של אידיאלים, אז הוא מחלק את אחד הגורמים. לצורך זה "מחלק" פירושו מכיל, כמו באידיאלים של חוג השלמים). הראינו שאידיאל הוא ראשוני אם ורק אם המנה ביחס אליו היא חוג ראשוני. מכאן שכל אידיאל מקסימלי הוא ראשוני. אידיאל האפס ראשוני אם ורק אם החוג ראשוני.

ראינו שהתמונה של אידיאל תחת הומומורפיזם אינה בהכרח אידיאל. לעומת זאת המקור של אידיאל הוא תמיד אידיאל. אם ההומומורפיזם הוא על, אז המקור של אידיאל ראשוני או מקסימלי הוא ראשוני או מקסימלי בהתאמה, אבל אם ההומומורפיזם אינו על זה לא בהכרח כך.

הבחנו שלכל n אידיאלים 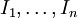$\ I_1,\dots,I_n$ בחוג, קיים שיכון 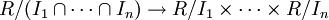$\ R/(I_1 \cap \cdots \cap I_n) \rightarrow R/I_1 \times \cdots \times R/I_n$. הגדרנו ששני אידיאלים I,J הם קו-מקסימליים אם סכומם הוא החוג כולו, וציטטנו את משפט השאריות הסיני, שלפיו אם 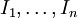$\ I_1,\dots,I_n$ קו-מקסימליים בזוגות, אז השיכון 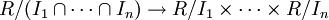$\ R/(I_1 \cap \cdots \cap I_n) \rightarrow R/I_1 \times \cdots \times R/I_n$ הוא על.

הרצאה שביעית

הוכחנו את משפט השאריות הסיני, בעזרת הצגת המספר 1 כצירוף האברים של אידיאלים מקסימליים. ההוכחה מבוססת על בניה של "וקטורי יחידה", שהם אברים של החוג המקורי, השקולים ל-1 מודולו אחד האידיאלים, ושקולים לאפס מודולו כל השאר.

כשמפעילים את המשפט על חוגים מהצורה 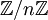$\ \mathbb{Z}/n\mathbb{Z}$ (כלומר מנות של חוג המספרים השלמים) מתברר שכל חוג כזה הוא מכפלה של חוגי מנה ביחס לחזקות של אידיאלים מקסימליים. הגדרנו מהו חוג מקומי (קומוטטיבי) - חוג שיש לו אידיאל מקסימלי יחיד - והראינו שכל חוג מהצורה 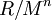$\ R/M^n$, כאשר M מקסימלי, הוא מקומי.

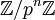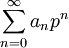את החוגים המקומיים קל לזהות לפי אוסף האברים הלא-הפיכים שלהם (שהוא אידיאל). בנוסף לדוגמאות מהצורה $\ \mathbb{Z}/p^n\mathbb{Z}$, ראינו שגם $\ F[[x]]$ הוא מקומי. אפשר לחקות את הבניה של החוג האחרון ולהגדיר את חוג השלמים ה-p-אדיים בתור חוג הסכומים הפורמליים $\ \sum_{n=0}^\infty a_n p^n$, כאשר המקדמים שלמים כלשהם. שני סכומים מייצגים את אותו איבר אם הם שקולים זה לזה מודולו כל חזקה של p. גם חוג השלמים ה-p-אדיים הוא מקומי: כל מספר שאינו מתחלק ב-p, הפיך שם (ויותר מזה: כאשר p אי-זוגי, לכל מספר שיש לו שורש מודולו p, יש גם שורש בחוג הזה).

כל חוג מקומי מלווה באופן טבעי בשדה - שדה השאריות (=חוג המנה) של החוג ביחס לאידיאל המקסימלי שלו.

הרצאה שמינית

שוחחנו קצת על חוגים סדורים ובמיוחד על שדות סדורים (שדות שמוגדר עליהם יחס סדר לינארי, כך שסכום או מכפלה של אברים חיוביים הם חיוביים). הקדשנו את עיקר השעור לבניה של חוג מעניין, R, עם מנה מקומית R/J, ששדה השאריות שלה הוא שדה סדור ארכימדי ושלם. לשדה הזה קוראים שדה המספרים הממשיים. R הוא החוג של כל סדרות-קושי מעל הרציונליים, J הוא האידיאל של הסדרות המתאפסות-לבסוף, והאידיאל המקסימלי של R/J כולל את כל הסדרות המתכנסות לאפס, מודולו J כמובן.

אגב, הנסיון להוכיח שה"אלכסון" של סדרת קושי של אברים של R/J מתכנס היה חסר תוחלת, משום שאף איבר קונקרטי של סדרה ב-R/J אינו מוגדר היטב: הרי אפשר לשנות בסדרה כזו מספר סופי של אברים מבלי להרגיש. ראו הוכחה מלאה ופרטים נוספים בחוברת (סוף סעיף 2.3 בגרסאות 1.1 ומעלה). בניית המספרים הממשיים אינה נכללת בחומר למבחן.