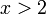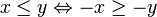88-611 אנליזה 1 למורים סמסטר א תשעו/מערכי תרגול/שיעור 1
תוכן עניינים
חזקות ושורשים
1) אם a הוא מספר כלשהוא ו-n מספר טבעי, אזי a בחזקת n מוגדר באופן הבא: 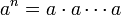 , מספר a נקרא בסיס
החזקה, מספר n נקרא מעריך החזקה.
, מספר a נקרא בסיס
החזקה, מספר n נקרא מעריך החזקה.
2) ניקח מספר ממשי חיובי x וניקח חזקה  כאשר n הוא מספר טבעי.נגדיר את x בחזקת
כאשר n הוא מספר טבעי.נגדיר את x בחזקת  להיות השורש ה-n-י של x:
להיות השורש ה-n-י של x: ![y=x^{\frac{1}{n}}=\sqrt[n]{x}](/images/math/2/5/9/259f18559f69a911aedba5f33c46fc93.png)
3) באופן כללי נגדיר חזקה רציונאלית באופן הבא: ![x^{\frac{p}{q}}=\left(\sqrt[q]{x}\right)^{p}](/images/math/0/e/e/0eec9697c289d642f384efe221ece676.png)
חוקי חזקות
- לכל x מתקיים
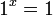
- לכל x מתקיים
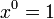 ובפרט
ובפרט 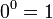
- לכל x שונה מאפס מתקיים
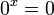
-
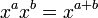
-
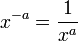
-
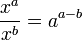
הגדרה: פונקציה מעריכית היא פונקציה מהצורה 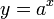 כאשר בסיס a הוא מספר קבוע.
כאשר בסיס a הוא מספר קבוע.
תרגיל: מצא את הפתרונות של המשוואה 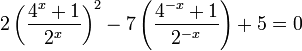
פתרון: ראשית נשים לב לכך ש: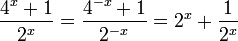 ולכן נסמן
ולכן נסמן 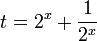 נציב את t במשוואה ונקבל
נציב את t במשוואה ונקבל 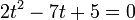 עם הפתרונות
עם הפתרונות
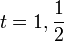 , לכן עלינו לפתור שתי משוואות:
, לכן עלינו לפתור שתי משוואות:
1) 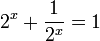 נעשה מכנה משותף ונקבל
נעשה מכנה משותף ונקבל 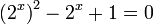 נסמן ב-
נסמן ב-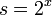 ונקבל משוואה
ונקבל משוואה 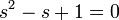 קל לראות שלמשוואה הזאת אין פתרון.
קל לראות שלמשוואה הזאת אין פתרון.
2) 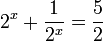 שוב נעשה מכנה משותף ונקבל
שוב נעשה מכנה משותף ונקבל 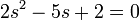 לאחר שנציב
לאחר שנציב 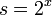 , פתרונות למשוואה הזאת הם
, פתרונות למשוואה הזאת הם 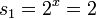 u> ו-
u> ו-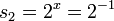 ולכן ה-x-ים שמקיימים את המשוואה הם
ולכן ה-x-ים שמקיימים את המשוואה הם 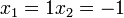
הגדרת הלוגריתם
לוגריתם של מספר x לפי בסיס a הוא b אם b הוא מעריך החזקה שבסיסה a וערכה x, כלומר 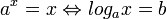 .
.
תכונות
אם 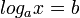 אזי:
אזי:
1) 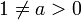
2) 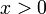
3) b מספר כלשהוא.
4) 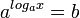
הגדרה: פונקציה לוגריתמית היא פונקציה מהצורה 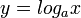 כאשר a הוא מספר קבוע חיובי ושונה מ-1 ותחום ההגדרה שלה הוא
כאשר a הוא מספר קבוע חיובי ושונה מ-1 ותחום ההגדרה שלה הוא 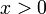 .
.
חוקי לוגריתמים
1) 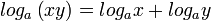
2) 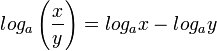
3) 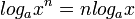
4) 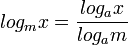
5) 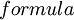 וגם
וגם 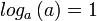
הערה: מקרה פרטי החשוב ביותר בו נתענין בקורס הוא 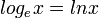 כאשר
כאשר 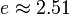
תרגיל: פתרו את 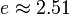 פתרון: נשתמש בחוקי הלוגריתמים
פתרון: נשתמש בחוקי הלוגריתמים 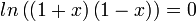 ואז נקבל
ואז נקבל 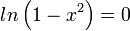 ואז לפי ההגדרה של הלוגריתם מקבלים
ואז לפי ההגדרה של הלוגריתם מקבלים 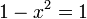 u> ולכן תושבה סופית היא היא x שווה אפס.
u> ולכן תושבה סופית היא היא x שווה אפס.
ערך מוחלט ואי שוויון
הגדרה: ערך מוחלט של מספר הוא המרחק שלו מנקודה אפס ומסמנים אותו בצורה הבאה:
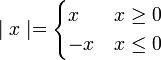
מרחק בין שתי נקודות מוגדר להיות 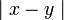
תכונות של ערך מוחלט
1) לכל x מתקיים 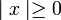
2) 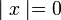 אם ורק אם
אם ורק אם 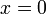
3) 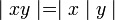
4) 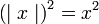
5) 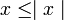
6) אי שוויון המשולש: 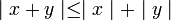
7) נניח ש-L מספר אי שלילי אזי 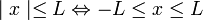
תכונות של אי שוויונים
- נניח ש-x,y אי שליליים אזי
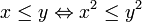
- נניח ש-x,y אי שליליים אזי
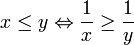
תרגיל: מצא עבור אילו ערכי x מתקיים אי השוויון הבא: 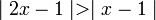
פתרון: מקרה ראשון: 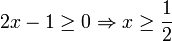 וגם
וגם 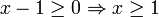
במקרה הזה נוריד את ערך מוחלט ונקבל 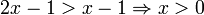 , חיתוך בין שלושת התחומים הוא
, חיתוך בין שלושת התחומים הוא 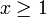 וזה פתרון במקרה 1.
וזה פתרון במקרה 1.
מקרה 2: 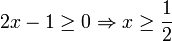 וגם
וגם 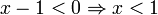 ולכן לאחר שנוריד את ערך מוחלט נוסיף מינוס לפני
ולכן לאחר שנוריד את ערך מוחלט נוסיף מינוס לפני 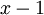 ונקבל
ונקבל 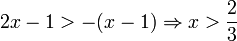 ולכן חיתוך בין שלושת התחומים הוא
ולכן חיתוך בין שלושת התחומים הוא 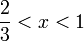
מקרה 3: 2x-1<0\Rightarrow x<\frac{1}{2} וגם 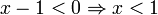 ולכן לאחר שנוריד את ערך מוחט נוסיף מינוס לפני כל אחד משלושת הביטויים ונקבל:
ולכן לאחר שנוריד את ערך מוחט נוסיף מינוס לפני כל אחד משלושת הביטויים ונקבל: 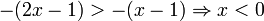
ולכן פתרון לאי שוויום יהיה איחוד של שלושת המקרים: 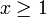 או
או 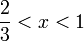 או
או 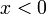
אי שוויונים מעריכיים
בפתרון של אי שוויונים מעריכיים יש לשים לב לכללים הבאים:
1) כל הבסיסים המופיעים באי שוויון חייבים להיות חיוביים.
2) * אם 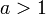 אזי אם
אזי אם 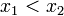 אז
אז 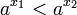 ולכן אי שוויון שבין החזקות זהה לאי שוויון שבין המעריכים.
ולכן אי שוויון שבין החזקות זהה לאי שוויון שבין המעריכים.
- אם
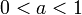 אזי אם
אזי אם 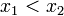 אז
אז 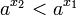 ולכן אי השוויון שבין החזקות הוא הפוך בכיוונו לאי השוויון שבין המעריכים.
ולכן אי השוויון שבין החזקות הוא הפוך בכיוונו לאי השוויון שבין המעריכים.
תרגיל: פתור את אי השוויון: 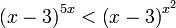
פתרון: כאן x מופיע גם בחזקה וגם בבסיס ולכן נצטרך לחלק לשני מקרים:
מקרה 1: 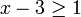 ולכן
ולכן 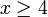 במקרה זה אי שוויון בין מעריכים הוא כמו אי שוויון בין החזקות ונקבל:
במקרה זה אי שוויון בין מעריכים הוא כמו אי שוויון בין החזקות ונקבל: 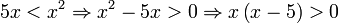 פתרון ואי שוויון זה הוא
פתרון ואי שוויון זה הוא 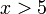 או
או 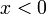 ולכן חיתוך בין שני התחומים הוא
ולכן חיתוך בין שני התחומים הוא 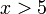
מקרה 2: 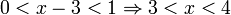 ואז אי שוויון שבין המעריכים הפוך בכיוונו לאי שוויון שבין החזקות ולכן מתקיים
ואז אי שוויון שבין המעריכים הפוך בכיוונו לאי שוויון שבין החזקות ולכן מתקיים 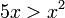 ותרון לאי שוויון זה הוא
ותרון לאי שוויון זה הוא 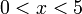 והפתרון המקרה זה יהיה חיתוך בין שני התחומים והוא
והפתרון המקרה זה יהיה חיתוך בין שני התחומים והוא 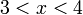
פתרון של אי שוויון יהיה איחוד בין שני המקרים: 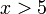 או
או 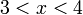
אי שוויונים לוגריתמיים
בפתרון של אי שוויונים לוגריתמיים יש לשים לב לכללים הבאים:
1) כל הביטויים שבתוך הלוגריתמים חייבים להיות חיוביים.
2) * אם 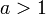 אזי אם
אזי אם 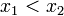 אזי
אזי 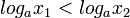 ואז אי שוויון שבין הלוגריתמים הוא באותו כיוון של אי שוויון שבין הביטויים שבתוך הלוגריתמים.
ואז אי שוויון שבין הלוגריתמים הוא באותו כיוון של אי שוויון שבין הביטויים שבתוך הלוגריתמים.
- אם
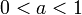 אז אם
אז אם 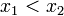 אז
אז 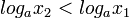 ואז אי שוויון שבין הלוגריתמים הפוך בכיוונו לאי שוויון שבין הביטויים שבתוך הלוגריתמים.
ואז אי שוויון שבין הלוגריתמים הפוך בכיוונו לאי שוויון שבין הביטויים שבתוך הלוגריתמים.
- אם x מופיע גם בבסיס הלוגריתם צריך לזכור שהבסיס הוא חיובי ושונה מ-1.
תרגיל: פתור את אי שוויון 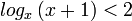
פתרון: קודם כל נסדר את הביטוי: 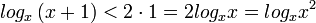 http://math-wiki.com/extensions/Math/images/button_math.png
קודם כל נדאג שביטויים בתוך הלוגריתם יהיו חיוביים
http://math-wiki.com/extensions/Math/images/button_math.png
קודם כל נדאג שביטויים בתוך הלוגריתם יהיו חיוביים 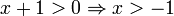 וגם
וגם 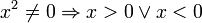 אבל יש לנו x בבסיס ואנחנו דורשים שהוא יהיה חיובי ולכן חיתוך בין שלושת התחומים נותן
אבל יש לנו x בבסיס ואנחנו דורשים שהוא יהיה חיובי ולכן חיתוך בין שלושת התחומים נותן 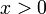 .
.
נחלק למקרים, מקרה 1: 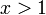 אזי
אזי 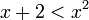 פתרון לאי שוויון ריבועי זה הוא
פתרון לאי שוויון ריבועי זה הוא 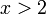 או
או 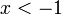 אבל ראינו ש-
אבל ראינו ש-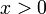 ולכן החיתוך בין התחומים כאן הוא
ולכן החיתוך בין התחומים כאן הוא 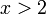 .
.
מקרה 2: אם 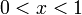 נקבל
נקבל 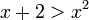 פתרון של אי שוויון ריבועי זה הוא
פתרון של אי שוויון ריבועי זה הוא 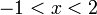 , סה"כ פתרון נוא חיתוך של התחומים והוא שווה
, סה"כ פתרון נוא חיתוך של התחומים והוא שווה 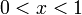 .
.
פתרון של אי שוויון הוא איחוד של שני המקרים והוא שווה ל-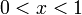 או
או