הבדלים בין גרסאות בדף "אנליזה מתקדמת למורים תרגול 2"
(←פתרון) |
(←פתרון) |
||
| שורה 45: | שורה 45: | ||
=====פתרון===== | =====פתרון===== | ||
| − | נתחיל עם הצמוד. מה אנחנו רוצים שיתקיים? נעבור רגע להצגה הקרטזית <math>z=r\cos \theta+r\sin \theta i</math>, ולכן <math>\overline{z}=r\cos \theta-r\sin \theta i</math>. הערך המוחלט לא משתנה, אנחנו רק צריכם למצוא זוית <math>\varphi</math> שתקיים לנו: <math>\cos \varphi=\cos \theta, \sin \varphi=-\sin \theta</math>. לצורך זה ניעזר בזהויות הבאות: <math>\sin(-\alpha)=-\sin \alpha,\cos(-\alpha)=\cos \alpha</math> | + | נתחיל עם הצמוד. מה אנחנו רוצים שיתקיים? נעבור רגע להצגה הקרטזית <math>z=r\cos \theta+r\sin \theta i</math>, ולכן <math>\overline{z}=r\cos \theta-r\sin \theta i</math>. הערך המוחלט לא משתנה, אנחנו רק צריכם למצוא זוית <math>\varphi</math> שתקיים לנו: <math>\cos \varphi=\cos \theta, \sin \varphi=-\sin \theta</math>. לצורך זה ניעזר בזהויות הבאות: <math>\sin(-\alpha)=-\sin \alpha,\cos(-\alpha)=\cos \alpha</math>, ולכן הבחירה <math>\varphi=-\theta</math> היא הבחירה המוצלחת! |
בדומה לזה נעשה עם <math>-z=-r\cos \theta-r\sin \theta i</math>. כאן אנחנו צריכים למצוא זוית <math>\varphi</math> שתקיים לנו: <math>\cos \varphi=-\cos \theta, \sin \varphi=-\sin \theta</math>. לצורך זה ניעזר בזהויות הבאות: | בדומה לזה נעשה עם <math>-z=-r\cos \theta-r\sin \theta i</math>. כאן אנחנו צריכים למצוא זוית <math>\varphi</math> שתקיים לנו: <math>\cos \varphi=-\cos \theta, \sin \varphi=-\sin \theta</math>. לצורך זה ניעזר בזהויות הבאות: | ||
גרסה מ־10:54, 6 בנובמבר 2018
חזרה ל מערכי תרגול.
תוכן עניינים
הצגה פולרית של מספרים מרוכבים
נתבונן במספר מרוכב 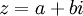 , נסמן ב
, נסמן ב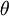 את הזוית עם הציר הממשי נגד השעון וב
את הזוית עם הציר הממשי נגד השעון וב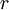 את הנורמה, אז נקבל:
את הנורמה, אז נקבל: 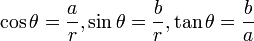 . ולכן נקבל
. ולכן נקבל 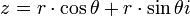 , שמסומן בקצרה:
, שמסומן בקצרה: 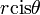 .
.
מעבר בין הצגות
מקרטזית לפולרית: בהינתן 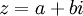 , ניקח
, ניקח 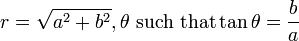 עד כדי הוספת
עד כדי הוספת 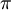 לפי מיקום המספר על הצירים.
לפי מיקום המספר על הצירים.
לדוגמא: עבור המספר 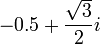 נקבל
נקבל 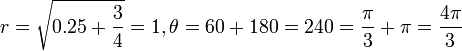 .
.
מפולרית לקרטזית: אם 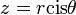 אז
אז 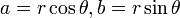 .
.
תרגיל
חשבו:
1. 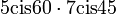 .
.
2. 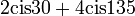 .
.
פתרון
1. הנורמה מוכפלת והזויות מתחברות: 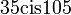
2. עוברים לקרטזית ושם מחברים: 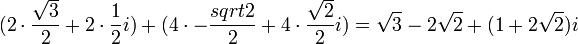
נוסחת דה-מואבר
מסקנה מכפל בהצגה פולרית נקבל: 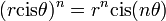 .
.
לדוגמא: 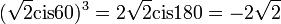 .
.
כך נוכל למצוא שורשים של מספרים מרוכבים. באופן כללי: אם 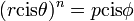 אז
אז ![r=\sqrt[n]{p}, n\cdot \theta=\phi + 2\pi k \Rightarrow \theta=\frac{\phi +2\pi k}{n}=\frac{\phi}{n}+\frac{2\pi k}{n}](/images/math/7/c/e/7ce287a3204a05da80ec87e1456db13f.png) .
.
תרגיל
חשב את ![\sqrt[3]{8\text{cis}\frac{\pi}{4}}](/images/math/b/1/b/b1bf956c42751ca642752e6026f40438.png)
פתרון
נקבל 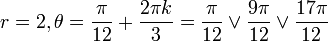 . נשים לב שאם ניקח
. נשים לב שאם ניקח 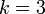 נקבל
נקבל 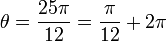 , ולכן זה בדיוק אותו מספר כמו עבור
, ולכן זה בדיוק אותו מספר כמו עבור 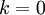 .
.
תרגיל - הצמוד בראי ההצגה הפולרית
נניח ש- 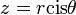 . מצאו את
. מצאו את 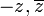 כתלות ב-
כתלות ב-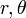 .
.
פתרון
נתחיל עם הצמוד. מה אנחנו רוצים שיתקיים? נעבור רגע להצגה הקרטזית 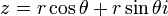 , ולכן
, ולכן 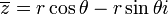 . הערך המוחלט לא משתנה, אנחנו רק צריכם למצוא זוית
. הערך המוחלט לא משתנה, אנחנו רק צריכם למצוא זוית 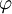 שתקיים לנו:
שתקיים לנו: 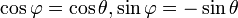 . לצורך זה ניעזר בזהויות הבאות:
. לצורך זה ניעזר בזהויות הבאות: 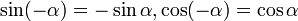 , ולכן הבחירה
, ולכן הבחירה 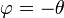 היא הבחירה המוצלחת!
היא הבחירה המוצלחת!
בדומה לזה נעשה עם 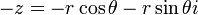 . כאן אנחנו צריכים למצוא זוית
. כאן אנחנו צריכים למצוא זוית 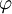 שתקיים לנו:
שתקיים לנו: 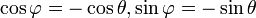 . לצורך זה ניעזר בזהויות הבאות:
. לצורך זה ניעזר בזהויות הבאות:
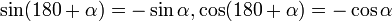 (הן נובעות מהזהויות של זוית משלימה ל180 והזהויות הקודמות), ולכן הבחירה
(הן נובעות מהזהויות של זוית משלימה ל180 והזהויות הקודמות), ולכן הבחירה 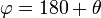 היא הבחירה המוצלחת!
היא הבחירה המוצלחת!
בסה"כ: 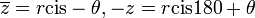 .
.
תרגיל
שורשים של פולינם
ראיתם בהרצאה שלכל פולינום, אם יש לו שורש מרוכב אז גם הצמוד שלו הוא שורש. בנוסף, המשפט היסודי של האלגברה אומר שכל פולינום מעל הממשיים מתפרק לגורמים ממשיים ממעלה 1 או 2. עכשיו נמצא פירוק כזה לפולינום פשוט.
תרגיל
פרקו את הפולינום: 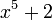 לגורמים ממשיים ממעלה 1 או 2.
לגורמים ממשיים ממעלה 1 או 2.
פתרון
ראשית נרשום את הפולינום כמשוואה במרוכבים: 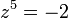 , ולצורך נוחות נעביר את המספר מימין להצגה פולרית:
, ולצורך נוחות נעביר את המספר מימין להצגה פולרית: 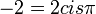 . עכשיו נשתמש בדה-מואבר: אנחנו מחפשים את כל המספרים המקיימים את המשוואה, ולכן מתקיים:
. עכשיו נשתמש בדה-מואבר: אנחנו מחפשים את כל המספרים המקיימים את המשוואה, ולכן מתקיים: ![z=\sqrt[5]{2}cis\frac{\pi}{5}+\frac{2\pi k}{5},k=0,\dots 4](/images/math/e/6/b/e6b2a36ef3ca8cf3ecc5e0a1f37fea0b.png) ...
...
כעת, ניקח מהשורשים את הממשיים (חייב להיות לפחת אחד, כי 5 מספר אי-זוגי), ואותם נשים בגורם מהצורה 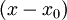 . לכל זוג שורשים מרוכבים (שורש והצמוד שלו), נמצא את הגורם ממעלה 2 המתאים להם המתקבל
ממכפלת הגורמים הליניאריים המרוכבים:
. לכל זוג שורשים מרוכבים (שורש והצמוד שלו), נמצא את הגורם ממעלה 2 המתאים להם המתקבל
ממכפלת הגורמים הליניאריים המרוכבים: 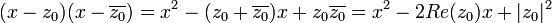 . וכאן כל המקדמים ממשיים.
. וכאן כל המקדמים ממשיים.
הזויות של השורשים הן: 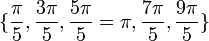 . הזוית היחידה שנותנת שורש ממשי היא
. הזוית היחידה שנותנת שורש ממשי היא 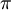 , וממנה נקבל את הגורם
, וממנה נקבל את הגורם ![(x+\sqrt[5]{2})](/images/math/c/a/4/ca4029ad55f8a2d4daae0922b7d4fc3a.png) .
.
הזוגות של הזוית הצמודות הן: 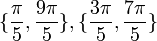 .
.
מהצמד הראשון נקבל את הגורם:
![(x-\sqrt[5]{2}\text{cis}\frac{\pi}{5})(x-\sqrt[5]{2}\text{cis}\frac{9\pi}{5})=x^2-2Re(\sqrt[5]{2}\text{cis}\frac{\pi}{5})x+\sqrt[5]{4}=x^2-2\cdot \sqrt[5]{2}\cos \frac{\pi}{5}+\sqrt[5]{4}](/images/math/a/8/8/a88511ea02517d13f3946341d839c716.png) .
.
מהצמד השני נקבל את הגורם:
![(x-\sqrt[5]{2}\text{cis}\frac{3\pi}{5})(x-\sqrt[5]{2}\text{cis}\frac{7\pi}{5})=x^2-2Re(\sqrt[5]{2}\text{cis}\frac{3\pi}{5})x+\sqrt[5]{4}=x^2-2\cdot \sqrt[5]{2}\cos \frac{3\pi}{5}+\sqrt[5]{4}](/images/math/1/a/b/1ab63628b3ffa4273447d1670ba0268e.png) .
.
כעת הפירוק הוא: ![x^5+2=(x+\sqrt[5]{2})(x^2-2\cdot \sqrt[5]{2}\cos \frac{\pi}{5}+\sqrt[5]{4})(x^2-2\cdot \sqrt[5]{2}\cos \frac{3\pi}{5}+\sqrt[5]{4})](/images/math/e/f/0/ef0171761043cd28f07cec0af88c6f89.png) .
.