אנליזה מתקדמת למורים תרגול 2

חזרה ל מערכי תרגול.

הצגה פולרית של מספרים מרוכבים

נתבונן במספר מרוכב 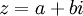$z=a+bi$, נסמן ב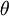$\theta$ את הזוית עם הציר הממשי נגד השעון וב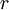$r$ את הנורמה, אז נקבל: 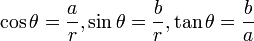$\cos \theta = \frac{a}{r},\sin \theta = \frac{b}{r}, \tan \theta = \frac{b}{a}$. ולכן נקבל 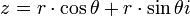$z=r\cdot \cos \theta +r\cdot \sin \theta i$, שמסומן בקצרה: $r\text{cis} \theta$.

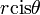מעבר בין הצגות

מקרטזית לפולרית: בהינתן 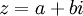$z=a+bi$, ניקח 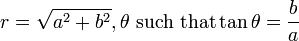$r=\sqrt{a^2+b^2},\theta \text{ such that} \tan \theta =\frac{b}{a}$ עד כדי הוספת 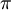$\pi$ לפי מיקום המספר על הצירים.

לדוגמא: עבור המספר 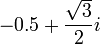$-0.5+\frac{\sqrt{3}}{2}i$ נקבל $r=\sqrt{0.25+\frac{3}{4}}=1,\theta=60+180=240=\frac{\pi}{3}+\pi=\frac{4\pi}{3}$.

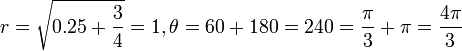מפולרית לקרטזית: אם 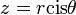$z=r\text{cis} \theta$ אז $a=r\cos \theta,b=r\sin \theta$.

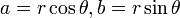תרגיל

חשבו:

1. $5\text{cis}60\cdot 7\text{cis}45$.

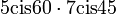2. $2\text{cis}30+4\text{cis}135$.

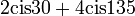פתרון

1. הנורמה מוכפלת והזויות מתחברות: 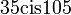$35\text{cis}105$

2. עוברים לקרטזית ושם מחברים: 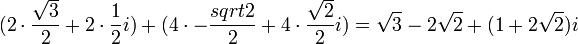$(2\cdot \frac{\sqrt{3}}{2}+2\cdot \frac{1}{2}i)+(4\cdot -\frac{sqrt{2}}{2} +4\cdot \frac{\sqrt{2}}{2}i)=\sqrt{3}-2\sqrt{2}+(1+2\sqrt{2})i$

נוסחת דה-מואבר

מסקנה מכפל בהצגה פולרית נקבל: 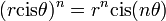$(r\text{cis} \theta )^n=r^n\text{cis} (n\theta)$.

לדוגמא: 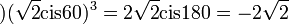$)(\sqrt{2}\text{cis}60)^3=2\sqrt{2}\text{cis}180=-2\sqrt{2}$.

כך נוכל למצוא שורשים של מספרים מרוכבים. באופן כללי: אם 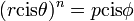$(r\text{cis}\theta)^n=p\text{cis}\phi$ אז $r=\sqrt[n]{p}, n\cdot \theta=\phi + 2\pi k \Rightarrow \theta=\frac{\phi +2\pi k}{n}=\frac{\phi}{n}+\frac{2\pi k}{n}$.

תרגיל

חשב את $\sqrt[3]{8\text{cis}\frac{\pi}{4}}$

פתרון

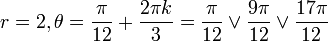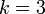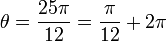נקבל $r=2,\theta=\frac{\pi}{12}+\frac{2\pi k}{3}=\frac{\pi}{12}\lor \frac{9\pi}{12}\lor \frac{17\pi}{12}$. נשים לב שאם ניקח $k=3$ נקבל $\theta=\frac{25\pi}{12}=\frac{\pi}{12}+2\pi$, ולכן זה בדיוק אותו מספר כמו עבור $k=0$.

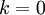שורשים של פולינם

תרגיל

פתרו: 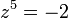$z^5=-2$.

פתרון

ראשית נרשום את המספר מימין בהצגה פולרית: 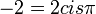$-2=2cis\pi$. עכשיו נשתמש בדה-מואבר: אנחנו מחפשים את כל המספרים המקיימים את המשוואה, ולכן מתקיים: $z=\sqrt[5]{2}cis\frac{\pi}{5}+\frac{2\pi k}{5},k=0,\dots 4$...

ראיתם בהרצאה שלכל פולינום, אם יש לו שורש מרוכב אז גם הצמוד שלו הוא שורש. בנוסף, המשפט היסודי של האלגברה אומר שכל פולינום מעל הממשיים מתפרק לגורמים ממעלה 1 או 2. נוכל להראות זאת בקצרה פה עבור הפולינום 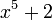$x^5+2$. ניקח מהשורשים את הממשיים (חייב להיות לפחת אחד, כי 5 מספר אי-זוגי), ואותם נשים בגורם מהצורה 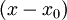$(x-x_0)$. לכל זוג שורשים מרוכבים (שורש והצמוד שלו), נמצא את הגורם ממעלה 2 המתאים לו ע"י בחירת המשוואה הריבועית המתוקנת (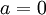$a=0$) ששורשיה מתקבלים מהנוסחה $\frac{-b\pm \sqrt{b^2-4c}}{2}$. כך נמצא את $b,c$.