דוגמא לחקר התכנסות טור עם פרמטר
תרגיל
קבע עבור אילו ערכי x הטור הבא מתכנס בהחלט/בתנאי/מתבדר:
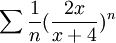
פתרון
דבר ראשון, נוכיח את הטענות הבאות:
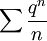 מתכנס בהחלט אם
מתכנס בהחלט אם 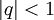 .
.
הוכחה:
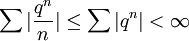
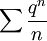 מתבדר אם
מתבדר אם 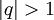
הוכחה:
נסמן 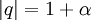 , כאשר
, כאשר 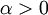 . לכן לפי אי שיוויון ברנולי
. לכן לפי אי שיוויון ברנולי 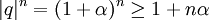
לכן 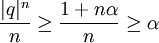 ולכן
ולכן 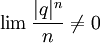 ולכן
ולכן 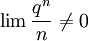 ולכן הטור וודאי מתבדר.
ולכן הטור וודאי מתבדר.
כעת, נסמן 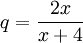 נותר לבדוק מתי |q| גדול מאחד, קטן מאחד או שווה ממש לאחד.
נותר לבדוק מתי |q| גדול מאחד, קטן מאחד או שווה ממש לאחד.
נפתור את אי השיוויון 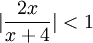 . קל לראות ש
. קל לראות ש 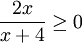 כאשר
כאשר 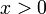 או
או 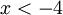 . במקרים אלה ניתן להוריד את הערך המוחלט ולפתור את אי השיוויון.
. במקרים אלה ניתן להוריד את הערך המוחלט ולפתור את אי השיוויון.
אם 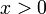 אזי
אזי 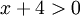 , ורוצים לפתור את אי השיוויון
, ורוצים לפתור את אי השיוויון 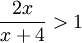 מותר לכפול ב(x+4) ולכן נקבל x>4. לכן סה"כ הטור מתבדר עבור x>4. עבור x<4 יוצא ש
מותר לכפול ב(x+4) ולכן נקבל x>4. לכן סה"כ הטור מתבדר עבור x>4. עבור x<4 יוצא ש  ולכן הטור מתכנס בהחלט עבור
ולכן הטור מתכנס בהחלט עבור 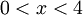
אם 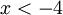 אזי
אזי 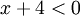 ולכן נכפול ב(x+4) ונחליף את כיוון אי השיוויון לקבל x<4. ביחד עם x<-4 נקבל שהטור מתבדר עבור x<-4. המקרה x>4 לא רלוונטי לנו במקרה זה.
ולכן נכפול ב(x+4) ונחליף את כיוון אי השיוויון לקבל x<4. ביחד עם x<-4 נקבל שהטור מתבדר עבור x<-4. המקרה x>4 לא רלוונטי לנו במקרה זה.
אם 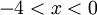 אזי צריך לפתור את אי השיוויון
אזי צריך לפתור את אי השיוויון 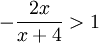 , שוב x+4 >0 ולכן מותר לכפול בו על מנת לקבל
, שוב x+4 >0 ולכן מותר לכפול בו על מנת לקבל 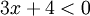 ולכן
ולכן 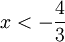 , ולכן עבור
, ולכן עבור 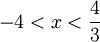 הטור מתבדר. עבור
הטור מתבדר. עבור 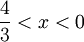 הטור מתכנס בהחלט.
הטור מתכנס בהחלט.
סיכום ביניים:
עבור 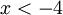 מתבדר
מתבדר
עבור 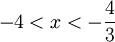 מתבדר
מתבדר
עבור 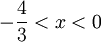 מתכנס בהחלט
מתכנס בהחלט
עבור 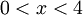 מתכנס בהחלט
מתכנס בהחלט
עבור  מתבדר
מתבדר
כל שנותר לעשות הוא לבדוק את מקרי הקצה 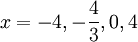
עבור 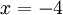 הטור כלל אינו מוגדר.
הטור כלל אינו מוגדר.
עבור 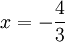 מקבלים את הטור
מקבלים את הטור 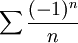 שהוא מתכנס בתנאי כידוע
שהוא מתכנס בתנאי כידוע
עבור 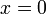 מקבלים את הטור של הסדרה הקבועה אפס שהוא בוודאי מתכנס בהחלט
מקבלים את הטור של הסדרה הקבועה אפס שהוא בוודאי מתכנס בהחלט
עבור 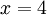 מקבלים את הטור ההרמוני
מקבלים את הטור ההרמוני 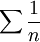 שהוא מתבדר.
שהוא מתבדר.
סיכום
עבור 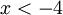 מתבדר
מתבדר
עבור 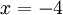 לא מוגדר
לא מוגדר
עבור 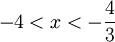 מתבדר
מתבדר
עבור 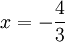 מתכנס בתנאי
מתכנס בתנאי
עבור 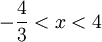 מתכנס בהחלט
מתכנס בהחלט
עבור 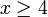 מתבדר
מתבדר