הבדלים בין גרסאות בדף "דוגמא לחקר התכנסות טור עם פרמטר"
(דף חדש: ==תרגיל== קבע עבור אילו ערכי x הטור הבא מתכנס בהחלט/בתנאי/מתבדר: <math>\sum\frac{1}{n}(\frac{2x}{x+4})^n</math> ==פתרון==) |
(←פתרון) |
||
| שורה 5: | שורה 5: | ||
==פתרון== | ==פתרון== | ||
| + | דבר ראשון, נוכיח את הטענות הבאות: | ||
| + | |||
| + | |||
| + | *<math>\sum\frac{q^n}{n}</math> מתכנס בהחלט אם <math>|q|<1</math>. | ||
| + | |||
| + | הוכחה: | ||
| + | <math>\sum|\frac{q^n}{n}|\leq \sum|q^n| < \infty</math> | ||
| + | |||
| + | |||
| + | |||
| + | *<math>\sum\frac{q^n}{n}</math> מתבדר אם <math>|q|>1</math> | ||
| + | |||
| + | הוכחה: | ||
| + | נסמן <math>|q|=1+\alpha</math>, כאשר <math>\alpha>0</math>. לכן לפי אי שיוויון ברנולי <math>|q|^n = (1+\alpha)^n \geq 1+n\alpha</math> | ||
| + | |||
| + | לכן <math>\frac{|q|^n}{n}\geq \frac{1+n\alpha}{n} \geq \alpha </math> ולכן <math>\lim \frac{|q|^n}{n} \neq 0</math> ולכן <math>\lim\frac{q^n}{n}\neq 0</math> ולכן הטור וודאי מתבדר. | ||
| + | |||
| + | |||
| + | |||
| + | כעת, נסמן <math>q=\frac{2x}{x+4}</math> נותר לבדוק מתי |q| גדול מאחד, קטן מאחד או שווה ממש לאחד. | ||
| + | |||
| + | |||
| + | נפתור את אי השיוויון <math>|\frac{2x}{x+4}| <1</math>. קל לראות ש <math>\frac{2x}{x+4}\geq 0</math> כאשר <math>x>0</math> או <math>x<-4</math>. במקרים אלה ניתן להוריד את הערך המוחלט ולפתור את אי השיוויון. | ||
| + | |||
| + | אם <math>x>0</math> אזי <math>x+4 >0 </math>, ורוצים לפתור את אי השיוויון <math>\frac{2x}{x+4} > 1</math> מותר לכפול ב(x+4) ולכן נקבל x>4. לכן סה"כ הטור מתבדר עבור x>4. עבור x<4 יוצא ש <math>\frac{2x}{x+4} < 1</math> ולכן הטור מתכנס בהחלט עבור <math>0<x<4</math> | ||
| + | |||
| + | אם <math>x<-4</math> אזי <math>x+4 <0 </math> ולכן נכפול ב(x+4) ונחליף את כיוון אי השיוויון לקבל x<4. ביחד עם x<-4 נקבל שהטור מתבדר עבור x<-4. המקרה x>4 לא רלוונטי לנו במקרה זה. | ||
| + | |||
| + | אם <math>-4<x<0</math> אזי צריך לפתור את אי השיוויון <math>-\frac{2x}{x+4} > 1</math>, שוב x+4 >0 ולכן מותר לכפול בו על מנת לקבל <math>3x+4<0</math> ולכן <math>x<-\frac{4}{3}</math>, ולכן עבור <math>-4<x<\frac{4}{3}</math> הטור מתבדר. עבור <math>\frac{4}{3}<x<0</math> הטור מתכנס בהחלט. | ||
גרסה מ־22:12, 21 בנובמבר 2010
תרגיל
קבע עבור אילו ערכי x הטור הבא מתכנס בהחלט/בתנאי/מתבדר:
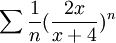
פתרון
דבר ראשון, נוכיח את הטענות הבאות:
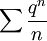 מתכנס בהחלט אם
מתכנס בהחלט אם 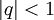 .
.
הוכחה:
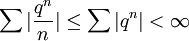
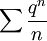 מתבדר אם
מתבדר אם 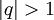
הוכחה:
נסמן 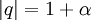 , כאשר
, כאשר 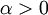 . לכן לפי אי שיוויון ברנולי
. לכן לפי אי שיוויון ברנולי 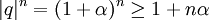
לכן 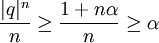 ולכן
ולכן 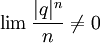 ולכן
ולכן 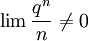 ולכן הטור וודאי מתבדר.
ולכן הטור וודאי מתבדר.
כעת, נסמן 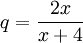 נותר לבדוק מתי |q| גדול מאחד, קטן מאחד או שווה ממש לאחד.
נותר לבדוק מתי |q| גדול מאחד, קטן מאחד או שווה ממש לאחד.
נפתור את אי השיוויון 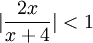 . קל לראות ש
. קל לראות ש 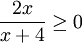 כאשר
כאשר 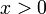 או
או 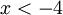 . במקרים אלה ניתן להוריד את הערך המוחלט ולפתור את אי השיוויון.
. במקרים אלה ניתן להוריד את הערך המוחלט ולפתור את אי השיוויון.
אם 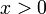 אזי
אזי 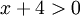 , ורוצים לפתור את אי השיוויון
, ורוצים לפתור את אי השיוויון 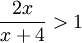 מותר לכפול ב(x+4) ולכן נקבל x>4. לכן סה"כ הטור מתבדר עבור x>4. עבור x<4 יוצא ש
מותר לכפול ב(x+4) ולכן נקבל x>4. לכן סה"כ הטור מתבדר עבור x>4. עבור x<4 יוצא ש  ולכן הטור מתכנס בהחלט עבור
ולכן הטור מתכנס בהחלט עבור 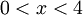
אם 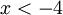 אזי
אזי 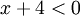 ולכן נכפול ב(x+4) ונחליף את כיוון אי השיוויון לקבל x<4. ביחד עם x<-4 נקבל שהטור מתבדר עבור x<-4. המקרה x>4 לא רלוונטי לנו במקרה זה.
ולכן נכפול ב(x+4) ונחליף את כיוון אי השיוויון לקבל x<4. ביחד עם x<-4 נקבל שהטור מתבדר עבור x<-4. המקרה x>4 לא רלוונטי לנו במקרה זה.
אם 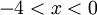 אזי צריך לפתור את אי השיוויון
אזי צריך לפתור את אי השיוויון 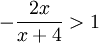 , שוב x+4 >0 ולכן מותר לכפול בו על מנת לקבל
, שוב x+4 >0 ולכן מותר לכפול בו על מנת לקבל 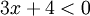 ולכן
ולכן 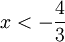 , ולכן עבור
, ולכן עבור 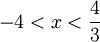 הטור מתבדר. עבור
הטור מתבדר. עבור 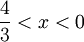 הטור מתכנס בהחלט.
הטור מתכנס בהחלט.