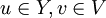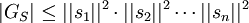היטל

הגדרה

יהי V מרחב מכפלה פנימית, ויהיו W תת מרחב של V ו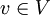$v\in V$ וקטור. ההגדרות הבאות למושג היטל v על המרחב W שקולות:

א. יהי 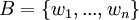$B=\{w_1,...,w_n\}$ בסיס אורתוגונלי לתת המרחב W, אזי ההיטל הינו 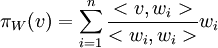$\pi_W(v)=\sum_{i=1}^n \frac{<v,w_i>}{<w_i,w_i>}w_i$ (התוצאה לא תלוייה בבחירת הבסיס)

ב. ההיטל הוא הוקטור 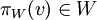$\pi_W(v)\in W$ המקיים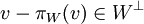 $v-\pi_W(v)\in W^\perp$

תרגילים

1

יהי V מרחב מכפלה פנימית מעל 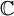$\mathbb{C}$ ממימד n ויהי 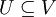$U\subseteq V$ תת מרחב ממימד k

א. הוכיחו כי לכל בסיס אורתונורמלי 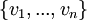$\{v_1,...,v_n\}$ למרחב V מתקיים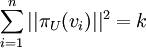 $\sum_{i=1}^n||\pi_U(v_i)||^2=k$

ב. יהי 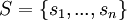$S=\{s_1,...,s_n\}$ בסיס כלשהו למרחב V ותהי 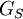$G_S$ מטריצת הגראם של S. הוכיחו כי:

$|G_S|\leq ||s_1||^2\cdot ||s_2||^2\cdots ||s_n||^2$

2

יהי V מרחב מכפלה פנימית ויהיו 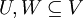$U,W\subseteq V$ תתי מרחבים כך ש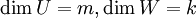 $\dim{U}=m, \dim{W}=k$

א. הוכיחו כי 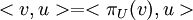$<v,u>=<\pi_U(v),u>$ לכל $u\in Y, v\in V$