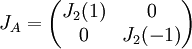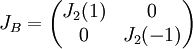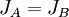|
|
| (4 גרסאות ביניים של 3 משתמשים אינן מוצגות) |
| שורה 1: |
שורה 1: |
| − | '''הערה:''' מי שיוסיף, לאחר הפתרון של אוהד להלן, פתרון סטנדרטי יותר לפי החוברת בנושא משפט ג'ורדן שהעליתי לאתר הקורס, יזכה גם הוא בנקודה על שאלה זו. (בועז)
| + | נתונות המטריצות <math>A=\begin{pmatrix} |
| | + | 1& 1 & 0 & 0\\ |
| | + | 0 & -1 & 1 & 0\\ |
| | + | 0 & 0 & 1 & 1\\ |
| | + | 0 & 0 & 0 & -1 |
| | + | \end{pmatrix} |
| | + | , B=\begin{pmatrix} |
| | + | 0 & 1 & 0 & 1\\ |
| | + | 1 & 0 & 0 & 0\\ |
| | + | 0 & 0 & 0 & 1\\ |
| | + | 0 & 0 & 1 & 0 |
| | + | \end{pmatrix}</math> האם הן דומות? הוכח את טענת. |
| | | | |
| − | התרגיל:
| + | כן הן דומות. נוכיח שצורת הג'ורדן של שתיהן שווה, ונקבל ש: <math>A\sim J_{A}=J_{B}\sim B</math> ומטרנזיטיביות של דמיון מטריצות נקבל ש <math>A\sim B</math> |
| − | נתונה המטר': <math>A=\begin{pmatrix}
| + | |
| − | 5 & 0 & 0 & 0 \\
| + | |
| − | 1 & 4 & 0 & 0\\
| + | |
| − | 2 & 3 & 3 & 0\\
| + | |
| − | 4 & 5 & 6 & 3
| + | |
| − | \end{pmatrix}</math>
| + | |
| | | | |
| − | א) מצא את צורת ז'ורדן של A
| + | נחשב את הפולינום האופייני של A, ונקבל כי <math>P_{A}(x)=(x+1)^{2}(x-1)^{2}</math> וגם כי הפולינום המינימלי של A שווה לפולינום האופייני ובסה"כ <math>M_{A}(x)=(x+1)^{2}(x-1)^{2}</math> |
| | | | |
| − | ב) מצא P הפיכה כך ש <math>P^{-1}AP</math> היא צורת ז'ורדן של A.
| + | במקרה זה, המטריצה הנ"ל מורכבת משני חלקי ג'ורדן (כאשר באחד <math>\lambda =1</math> ובשני <math>\lambda =-1</math>), וכל אחד מהם בגודל 2. |
| | | | |
| − | מקור: [http://u.cs.biu.ac.il/~tsaban/LinearAlgebra/Exams/HU_LA2/80135_2009_2_1_1.pdf]
| + | מכיון שבשניהם הבלוק הגדול ביותר הוא מגודל 2, נקבל כי צורת הגורדן היא |
| | | | |
| − | '''פתרון:'''
| + | <math>J_{A}=\begin{pmatrix} |
| − | נתבונן בפולינום האופייני של A (שהוא קל לחישוב, מטר' משולשית): <math>P_A(x) = (x-5)(x-4)(x-3)^{2}</math> לפי משפט, אותם גורמים לינאריים בדיוק יופיעו בפולינום המינימלי של A.
| + | J_{2}(1) & 0\\ |
| − | ברור שהריבוי הגיאומטרי של הע"ע 4,5 הוא 1. כמו כן הגורמים <math>x-4,x-5</math> יופיעו בפולינום המינימלי של A [לפי משפט], והמעלה שלהם לא תיהיה גדולה מ 1 כי פולינום מינימלי מחלק כל פולינום שמאפס את A, ובפרט את הפולינום האופייני, לפי משפט קיילי המילטון.
| + | 0 & J_{2}(-1) |
| − | לכן לפי משפט, הבלוקים הגדולים ביותר ביותר המתאימים לע"ע 4,5 הם בגודל של החזקה של <math>x-4,x-5</math> בפולינום המינימלי של A, בהתאמה. ולפי מה שאמרנו זה יהיה שווה בדיוק 1.
| + | \end{pmatrix}</math> |
| − | לכן צורת ז'ורדן של A היא משהו בסגנון של <math>J_1(5) \oplus J_1(4) \oplus B</math>
| + | |
| | | | |
| − | כמו כן, אין עוד בלוקים המתאימים לע"ע 4,5 כי הריבוי הגיאומטרי שלהם הוא בדיוק 1 = כמות הבלוקים שלהם בצורת ז'ורדן.
| + | נעשה אותו הדבר למטריצה B, ונקבל כי יש לה אותו פולינום אופייני ואותו פולינום מינימלי, ולכן <math>J_{B}=\begin{pmatrix} |
| − | סך הבלוקים המתאימים לע"ע 3 הוא (ריבוי גאומטרי) כמימד מרחב האיפוס של <math>A-3I = \begin{pmatrix}
| + | J_{2}(1) & 0\\ |
| − | 2 & 0 & 0 & 0 \\ | + | 0 & J_{2}(-1) |
| − | 1 & 1 & 0 & 0\\
| + | |
| − | 2 & 3 & 0 & 0\\ | + | |
| − | 4 & 5 & 6 & 0
| + | |
| | \end{pmatrix}</math> | | \end{pmatrix}</math> |
| − | וזו מטר' מדורגת מדרגה 3 מסדר 4, ולכן מימד מרחב האיפוס שלה הוא בדיוק 1, ולכן סה"כ צורת ז'ורדן של A היא: <math>G = J_1(5) \oplus J_1(4) \oplus J_2(3)</math>
| |
| | | | |
| | + | וקבלנו כי <math>J_{A}=J_{B}</math> |
| | | | |
| − | | + | מ.ש.ל. |
| − | ב) נסמן את העמודות של P ב (v1,v2,v3,v4) בהתאמה. אזי: <math>G = P^{-1}AP</math> ולכן <math>PG=AP</math> ולכן לכל i רלוונטי <math>P*Ci(G) = A*v_i</math>.
| + | |
| − | | + | |
| − | אז עבור i = 1,2 זה ממש קל כי אנחנו רק צריכים למצוא וקטורים עצמיים שמתאימים לע"ע 4,5... ברור שאנחנו יודעים לעשות את זה, לכן אני אחסוך לכולם[חוץ מלעצמי] חישוב מפרך ונגיע ל <math>v_1 = (2, 2, 5, 24), v_2 = (0, 1, 3, 23)</math>
| + | |
| − | נקבל לפי הנ"ל גם את המשוואות הבאות: <math>3v_3=Av_3, v_3 + 3v_4=Av_4</math> נעביר קצת אגפים ונקבל: <math>v_3 \in N(A-3I), v_3 = (A-3I)v_4 \in C(A-3I)</math> כאשר N מציין את מרחב האיפוס ו C מציין את מרחב העמודות.
| + | |
| − | | + | |
| − | כבר כתבנו למעלה את A-3I אז אפשר להסתכל עליה.
| + | |
| − | | + | |
| − | כבר אמרנו גם שמימד המרחב העצמי של הע"ע 3 הוא 1, ולכן ל <math>v_3</math> יש לנו רק אפשרות אחת (עד כדי כפל בסקלר שלא מעניין אותנו פה), ממש קל לראות שאותו וקטור הוא <math>v_3=(0, 0, 0, 1)</math>
| + | |
| − | ולכן קיבלנו משוואה: <math>(A-3I)v_4=v_3 = e_4 = (0, 0, 0, 1)</math> זו משוואה פשוטה למדי בארבעה נעלמים שאפשר לפתור עם דירוג [אגב, אין לזה פתרון יחיד]: <math>v_4 = (0, 0, \frac{1}{6}, a)</math> אבל נבחר a = 0 שיהיה נוח לכולם... <math>v_4 = (0, 0, \frac{1}{6}, 0)</math>
| + | |
| − | | + | |
| − | סוף סוף קיבלנו את <math>P = \begin{pmatrix}
| + | |
| − | 2 & 0 & 0 & 0 \\
| + | |
| − | 2 & 1 & 0 & 0\\
| + | |
| − | 5 & 3 & 0 & \frac{1}{6}\\
| + | |
| − | 24 & 23 & 1 & 0
| + | |
| − | \end{pmatrix}</math>
| + | |
| − | זה מגניב כי אם נחליף את שורה 3,4 אנחנו רואים ש P היא הפיכה [דרגה 4], אז לא דיברנו שטויות לגמרי, יש ניצוץ של תקווה... טוב נו, אם בודקים זה אכן יוצא נכון [סתם עבודה טכנית, שלצערי עשיתי אותה]
| + | |
כן הן דומות. נוכיח שצורת הג'ורדן של שתיהן שווה, ונקבל ש: 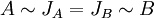 ומטרנזיטיביות של דמיון מטריצות נקבל ש
ומטרנזיטיביות של דמיון מטריצות נקבל ש 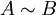
נעשה אותו הדבר למטריצה B, ונקבל כי יש לה אותו פולינום אופייני ואותו פולינום מינימלי, ולכן 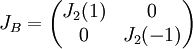
מ.ש.ל.
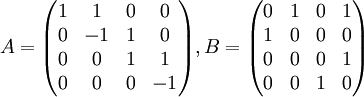 האם הן דומות? הוכח את טענת.
האם הן דומות? הוכח את טענת.
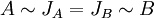 ומטרנזיטיביות של דמיון מטריצות נקבל ש
ומטרנזיטיביות של דמיון מטריצות נקבל ש 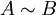
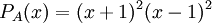 וגם כי הפולינום המינימלי של A שווה לפולינום האופייני ובסה"כ
וגם כי הפולינום המינימלי של A שווה לפולינום האופייני ובסה"כ 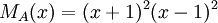
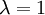 ובשני
ובשני 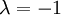 ), וכל אחד מהם בגודל 2.
), וכל אחד מהם בגודל 2.