הבדלים בין גרסאות בדף "88-240 משוואות דיפרנציאליות רגילות סמסטר א תשעב"
(←קישורים) |
(←הודעות) |
||
| (22 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 7: | שורה 7: | ||
'''[[88-240 משוואות דיפרנציאליות רגילות סמסטר א תשעב/מערך תרגול|מערכי התרגול]]''' | '''[[88-240 משוואות דיפרנציאליות רגילות סמסטר א תשעב/מערך תרגול|מערכי התרגול]]''' | ||
| + | |||
| + | [http://www.math-wiki.com/images/0/0d/Green_boundary.pdf שיטת גרין עבור בעיית שפה] | ||
| + | |||
| + | [http://www.math-wiki.com/images/5/50/Annihilator_Method.doc קובץ הסבר על שיטת המשמיד (באנגלית)] | ||
| + | |||
| + | [http://www.vibrationdata.com/math/Laplace_Transforms.pdf טבלה של התמרות לפלס - יש גם דברים שלא למדנו] | ||
| + | |||
| + | [http://www.math-wiki.com/images/d/d1/T11s.pdf פתרון תרגיל 11] | ||
| + | |||
| + | [http://www.math-wiki.com/images/9/92/Odegradespdf.pdf ציוני תרגיל] | ||
=הודעות= | =הודעות= | ||
| + | '''חשוב: תאריך ההגשה של תרגיל 8 הוא עד יום ראשון הקרוב בשעה 12:00 לתא של פרופ' שיף (113)''' --[[משתמש:Michael|Michael]] 18:02, 4 בינואר 2012 (IST) | ||
| + | |||
| + | העלתי קובץ ובו פתרון של בעיית שפה לפי שיטת גרין. | ||
| + | שימו לב שמדובר כאן על תנאי שפה מסויימים, נא לא להתבלבל. | ||
| + | --[[משתמש:Michael|Michael]] 20:24, 27 בנובמבר 2011 (IST) | ||
| + | |||
| + | העלתי את פתרון תרגיל 11 ואת ציוני התרגילים. מי שמוצא טעות נא להודיע לי --[[משתמש:Michael|Michael]] 20:28, 22 בפברואר 2012 (IST) | ||
| + | ---- | ||
| + | לגבי התרגול היום (6.12.2011): | ||
| + | הגענו לפתרון <math>y=c_1\cos{\omega_0t}+c_2\sin{\omega_0t}+\frac{\cos{\omega t}}{\omega_0^2-\omega^2}</math> | ||
| + | |||
| + | ומשם בלי ממש להסביר איך, שינינו קצת את <math>c_1</math> כדי שהגבול יתכנס. | ||
| + | הדרך המלאה היא כך: | ||
| + | |||
| + | <math>y(0)=c_1+\frac{1}{\omega_0^2-\omega^2}</math> | ||
| + | |||
| + | <math>y'(0)=\omega_0 c_2</math> | ||
| + | |||
| + | (לא קשה לראות שזה נכון). אפשר לבודד את הקבועים: | ||
| + | |||
| + | <math>c_1=y(0)-\frac{1}{\omega_0^2-\omega^2}</math> | ||
| + | |||
| + | <math>c_2=\frac{y'(0)}{\omega_0}</math> | ||
| + | |||
| + | ולכן הפתרון הוא: | ||
| + | |||
| + | <math>y=(y(0)-\frac{1}{\omega_0^2-\omega^2})\cos{\omega_0 t}+\frac{y'(0)}{\omega_0}\sin{\omega_0 t}+\frac{\cos{\omega t}}{\omega_0^2-\omega^2}</math> | ||
| + | |||
| + | <math>=y(0)\cos{\omega_0 t}+\frac{y'(0)}{\omega_0}\sin{\omega_0 t}+\frac{\cos{\omega t}-\cos{\omega_0 t}}{\omega_0^2-\omega^2}</math> | ||
| + | |||
| + | עכשיו נוכל להשאיף <math>\omega \rightarrow \omega_0</math> ולקבל (תוך כדי שימוש בכלל לופיטל): | ||
| + | |||
| + | <math>y=A_1\cos{\omega_0 t}+A_2\sin{\omega_0 t}+\lim_{\omega \rightarrow \omega_0}\frac{\frac{d}{d \omega} (\cos{\omega t}-\cos{\omega_0 t})}{\frac{d}{d \omega} (\omega_0^2-\omega^2)}=</math> | ||
| + | |||
| + | <math>=A_1\cos{\omega_0 t}+A_2\sin{\omega_0 t}+\lim_{\omega \rightarrow \omega_0} \frac{-t \sin{\omega t}}{-2\omega}=A_1\cos{\omega_0 t}+A_2\sin{\omega_0 t}+\frac{t \sin{\omega_0 t}}{2\omega_0}</math> | ||
| + | |||
| + | כאשר: | ||
| + | |||
| + | <math>A_1=y(0)</math> ו- <math>A_2=\frac{y'(0)}{\omega_0}</math> הם קבועים חופשיים. | ||
| + | |||
| + | רצוי מאוד שתשתמשו בדרך המלאה הזו, ולא בדרך הקצרה יותר שלמדנו היום. | ||
| + | --[[משתמש:Michael|Michael]] 22:53, 6 בדצמבר 2011 (IST) | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | |||
| + | בתרגול היום דיברנו על מערכות הומוגניות עם מקדמים קבועים: | ||
| + | הדבר הראשון שצריכים לעשות הוא למצוא ע"ע. | ||
| + | |||
| + | למקרה שתתקלו במד"ר בספרות, כדאי שתדעו את השמות של המקרים שנתקלנו בהם. | ||
| + | |||
| + | המקרה הראשון היה ע"ע פשוט ממשי - simple real eigenvalue | ||
| + | |||
| + | המקרה השני היה זוג ע"ע מרוכבים פשוטים - simple complex conjugate pair eigenvalues | ||
| + | |||
| + | המקרה השלישי היה ע"ע מריבוי אלגברי גבוה m שבכל זאת (למזלנו) ניתן למצוא לו m וקטורים עצמיים. לע"ע שכזה קוראים ע"ע שלם - complete eigenvalue | ||
| + | |||
| + | והמקרה הכי פחות קל, ע"ע מריבוי גבוה m שיש לו '''פחות''' מ-m ו"ע. ע"ע כזה נקרא ע"ע דפקטיבי - defective eigenvalue | ||
| + | |||
| + | פתרון יותר מפורט של המקרה האחרון: | ||
| + | |||
| + | רצינו לפתור את המד"ר | ||
| + | <math>\vec{y}=A \vec{y}</math>, כאשר <math>A=\begin{pmatrix} 2 & 1\\ 0 & 2 \end{pmatrix}</math> | ||
| + | |||
| + | ל-A יש רק ע"ע אחד <math>\lambda=2</math>. נחפש ו"ע <math>\vec{v}=\begin{pmatrix} a\\ b \end{pmatrix}</math>: | ||
| + | |||
| + | <math>A \vec{v}=\lambda \vec{v}</math> | ||
| + | |||
| + | <math>A \vec{v}=2 \vec{v}</math> | ||
| + | |||
| + | <math>(2I-A)\vec{v}=0</math> | ||
| + | |||
| + | <math>\begin{pmatrix} 0 & -1\\ 0 & 0 \end{pmatrix} \vec{v}=0</math> | ||
| + | |||
| + | מקבלים את התנאי <math>b=0</math> וניתן לקחת <math>a=0</math> ולקבל ו"ע <math>\vec{v}=\begin{pmatrix} 1\\ 0 \end{pmatrix}</math> ולכן את הפתרון הקלאסי : | ||
| + | |||
| + | <math>\vec{v} e^{\lambda t}=\begin{pmatrix} 1\\ 0 \end{pmatrix} e^{2t}</math> | ||
| + | |||
| + | נראה שאין תקווה כי אי אפשר לבנות עוד פתרון כזה. אבל צריכים לחפש פתרון מהצורה <math>\vec{y}=e^{2t} \left( \begin{pmatrix} a\\b \end{pmatrix}t+ \begin{pmatrix} c\\d \end{pmatrix} \right)</math>. | ||
| + | |||
| + | מצד אחד: | ||
| + | |||
| + | <math>\vec{y}'=\left[e^{2t} \begin{pmatrix} at+c\\bt+d \end{pmatrix}\right] '=2e^{2t}\begin{pmatrix} at+c\\bt+d \end{pmatrix}+e^{2t}\begin{pmatrix} a\\b \end{pmatrix}=e^{2t}\begin{pmatrix} 2at+2c+a\\2bt+2d+b \end{pmatrix}</math> | ||
| + | |||
| + | ומצד שני: | ||
| + | |||
| + | <math>A \vec{y}=\begin{pmatrix} 2 & 1\\ 0&2 \end{pmatrix}\left[ e^{2t} \begin{pmatrix} at+c\\bt+d \end{pmatrix}\right]=e^{2t} \begin{pmatrix} 2at+2c+bt+d\\ 2bt+2d\end{pmatrix}</math> | ||
| + | |||
| + | כדי לקבל שוויון ביניהם, נצטרך: | ||
| + | |||
| + | <math>a=d</math> | ||
| + | |||
| + | <math>b=0</math> | ||
| + | |||
| + | (<math>c</math> נשאר חופשי) | ||
| + | |||
| + | נציב זאת בניחוש ונקבל: | ||
| + | |||
| + | <math>\vec{y}=e^{2t} \left( \begin{pmatrix} a\\0 \end{pmatrix}t+\begin{pmatrix} c\\a \end{pmatrix}\right)=e^{2t} \begin{pmatrix} at+c\\a \end{pmatrix}=a \begin{pmatrix} t\\1 \end{pmatrix} e^{2t}+c \begin{pmatrix} 1\\0 \end{pmatrix} e^{2t}=c_1 \begin{pmatrix} 1\\0 \end{pmatrix} e^{2t}+c_2 \begin{pmatrix} t\\1 \end{pmatrix} e^{2t}</math> | ||
| + | |||
| + | בתרגול לקחתי c=0 ו-a=1 ובניתי פתרון נוסף שבכל מקרה הצטרף לפתרון הראשוני. סליחה על הבלבול. | ||
| + | |||
| + | --[[משתמש:Michael|Michael]] 21:50, 22 בדצמבר 2011 (IST) | ||
| + | |||
| + | למרות שראיתם בהרצאה דוגמה לפתרון מערכת לא הומוגנית אני חושב שכדאי שאפתור עוד אחת כאן. נניח שרוצים לפתור את: | ||
| + | |||
| + | <math>\vec{y}'=\underbrace{\begin{pmatrix} 4 & -3\\8 & -6 \end{pmatrix}}_{A(t)} \vec{y}+\underbrace{\begin{pmatrix} t\\ e^t \end{pmatrix}}_{\vec{b}(t)}</math> | ||
| + | |||
| + | הדבר הראשון שצריכים לעשות הוא למצוא מטריצה יסודית כלשהי, בתרגול ראינו למשל את המטריצה: | ||
| + | |||
| + | <math>Y(t)=\begin{pmatrix} 3 & e^{-2t}\\4 & 2e^{-2t} \end{pmatrix}</math> | ||
| + | |||
| + | השלב הבא הוא לחשב את המטריצה ההופכית, המחשב נתן לי: | ||
| + | |||
| + | <math>Y^{-1}(t)=\begin{pmatrix} 1 & -\frac{1}{2}\\ -2e^{2t} & \frac{3e^{2t}}{2} \end{pmatrix}</math> | ||
| + | |||
| + | נחשב עכשיו את <math>Y^{-1}(t) \vec{b}(t)</math>: | ||
| + | |||
| + | <math>Y^{-1}(t) \vec{b}(t)=\begin{pmatrix} 1 & -\frac{1}{2}\\ -2e^{2t} & \frac{3e^{2t}}{2} \end{pmatrix} \begin{pmatrix} t\\ e^t \end{pmatrix}=\left( | ||
| + | \begin{array}{c} | ||
| + | t-\frac{e^t}{2} \\ | ||
| + | \frac{3 e^{3 t}}{2}-2 e^{2 t} t | ||
| + | \end{array} | ||
| + | \right) </math> | ||
| + | |||
| + | ניקח אינטגרל (אינטגרל של וקטור עושים רכיב-רכיב): | ||
| + | |||
| + | <math>\int{Y^{-1}(t) \vec{b}(t) dt}=\left( | ||
| + | \begin{array}{c} | ||
| + | \frac{t^2}{2}-\frac{e^t}{2}+k_1 \\ | ||
| + | -e^{2 t} t+\frac{e^{2 t}}{2}+\frac{e^{3 t}}{2}+k_2 | ||
| + | \end{array} | ||
| + | \right)=\left( | ||
| + | \begin{array}{c} | ||
| + | \frac{t^2}{2}-\frac{e^t}{2} \\ | ||
| + | -e^{2 t} t+\frac{e^{2 t}}{2}+\frac{e^{3 t}}{2} | ||
| + | \end{array} | ||
| + | \right)+\begin{pmatrix} k_1\\k_2 \end{pmatrix}</math> | ||
| + | |||
| + | כל מה שנותר לעשות הוא להכפיל במטריצה יסודית: | ||
| + | |||
| + | <math>Y(t)( \int{Y^{-1}(t) \vec{b}(t) dt}+\vec{k})= | ||
| + | \left( | ||
| + | \begin{array}{c} | ||
| + | \frac{3 t^2}{2}-t-e^t+\frac{1}{2} \\ | ||
| + | 2 t^2-2 t-e^t+1 | ||
| + | \end{array} | ||
| + | \right)+k_1 \begin{pmatrix} 3\\4 \end{pmatrix}+k_2 \begin{pmatrix} e^{-2t}\\2e^{-2t} \end{pmatrix}</math> | ||
| + | |||
| + | זהו בדיוק הפתרון הכללי של המערכת <math>(\vec{y})</math>. אם היה נתון תנאי התחלה היינו צריכים למצוא את הקבועים החופשיים. | ||
| + | --[[משתמש:Michael|Michael]] 01:49, 27 בדצמבר 2011 (IST) | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | לגבי סוף התרגול היום: עסקנו במשוואה <math>4xy''+2y'+y=0</math>. המשוואה האינדנציאלית נתנה לנו שני ערכים מותרים עבור <math>\alpha</math>: <math>\alpha_{1,2}=0,\frac{1}{2}</math> הגענו לפתרון אחד כאשר לקחנו <math>\alpha=0</math>: | ||
| + | |||
| + | <math>y_1=a_0 \sum_{n=0}^\infty{\frac{(-1)^n}{2n!} x^n}</math> | ||
| + | אמרנו שאם מדובר בתחום שבו x>0 ניתן לרשום אותו בצורה: | ||
| + | |||
| + | <math>y_1=a_0 \cos{\sqrt{x}}</math> | ||
| + | נגיע עכשי לפתרון השני, ניקח הפעם את <math>\alpha=\frac{1}{2}</math>. הרקורסיה שלנו היא | ||
| + | |||
| + | <math>a_{n+1}=\frac{-a_n}{2(n+\frac{3}{2})(2n+2)}=\frac{-a_n}{(2n+2)(2n+3)}</math> | ||
| + | |||
| + | נמצא קצת מהמקדמים: | ||
| + | |||
| + | <math>a_1=\frac{-a_0}{2*3}</math> | ||
| + | |||
| + | <math>a_2=\frac{-a_1}{4*3}=\frac{a_0}{5*4*3*2}</math> | ||
| + | |||
| + | <math>a_3=\frac{-a_2}{7*6}=\frac{-a_0}{7!}</math> | ||
| + | |||
| + | כבר ניתן לנחש: | ||
| + | |||
| + | <math>a_n=\frac{a_0 (-1)^n}{(2n+1)!}</math> | ||
| + | |||
| + | אם כך, נקבל פתרון שני: | ||
| + | |||
| + | <math>y_2=x^\alpha \sum_{n=0}^\infty {a_n x^n}=x^\frac{1}{2} \sum_{n=0}^\infty {\frac{a_0 (-1)^n}{(2n+1)!} x^n}=\sum_{n=0}^\infty {\frac{a_0 (-1)^n}{(2n+1)!} x^{n+\frac{1}{2}}}</math> | ||
| + | |||
| + | אם x חיובי נוכל לרשום אותו בצורה: | ||
| + | |||
| + | <math>y_2=\sum_{n=0}^\infty {\frac{a_0 (-1)^n}{(2n+1)!} \sqrt{x}^{2n+1}}=a_0 \sin{\sqrt{x}}</math> | ||
| + | |||
| + | הפתרון הכללי יהיה צירוף לינארי שלהם: | ||
| + | |||
| + | <math>y=c_1 y_1+c_2 y_2=C_1 \sum_{n=0}^\infty {\frac{(-1)^n}{(2n)!} x^n}+C_2 \sum_{n=0}^\infty {\frac{(-1)^n}{(2n+1)!} x^{n+\frac{1}{2}}}</math> | ||
| + | |||
| + | כאשר הקבועים הגדולים בלעו את <math>a_0</math> | ||
| + | |||
| + | הערה חשובה: שימו לב שלא תמיד ניתן לפתור את הרקורסיות (אפילו לא במונחים של פונקציית גמא). במקרה כזה רצוי שלפחות תפתחו את הטור לכמה איברים ראשונים. | ||
| + | |||
| + | --[[משתמש:Michael|Michael]] 01:37, 3 בינואר 2012 (IST) | ||
| + | |||
| + | |||
| + | ---- | ||
| + | |||
| + | הנה דוגמא של מד"ר, כאשר אגף ימין הוא מוגדר למקוטעין: | ||
| + | |||
| + | <math>y''=\begin{cases} 2t & 0 \le t \le \frac{1}{2} \\ 2-2t & \frac{1}{2} \le t \le 1 \end{cases}=f(t), y(0)=y'(0)=0</math> | ||
| + | |||
| + | "כזכור", ניתן לרשום פונקצייה מוגדרת למקוטעין בעזרת פונקציית הביסייד עם שני פרמטרים כך: | ||
| + | |||
| + | <math>f(t)=2t H_{0,\frac{1}{2}}(t)+(2-2t) H_{\frac{1}{2},1}(t)</math> | ||
| + | |||
| + | (האמת שיש כאן קצת בלוף: יש בעיה בנקודות ה"תפירה" <math>t=\frac{1}{2}</math>. לא אמרנו מה קורה לפונקציית הביסייד באפס. אבל בכל מקרה, להתמרת לפלס לא ממש אכפת מה קורה בנקודה בודדת) | ||
| + | |||
| + | נפשט קצת את <math>f(t)</math>: | ||
| + | |||
| + | <math>f(t)=2t (H(t-0)-H(t-\frac{1}{2})+(2-2t) (H(t-\frac{1}{2})-H(t-1))=2t H(t)+(2-2t-2t) H(t-\frac{1}{2})-(2-2t) H(t-1)=</math> | ||
| + | |||
| + | <math>=2tH(t)-4 (t-\frac{1}{2})H(t-\frac{1}{2})+2 (t-1)H(t-1)</math> | ||
| + | |||
| + | נגדיר פונקצייה נוספת לנוחיותנו: | ||
| + | |||
| + | <math>g(t)=t</math> | ||
| + | |||
| + | ואז ניתן לרשום: | ||
| + | |||
| + | <math>f(t)=2g(t)H(t)-4g(t-\frac{1}{2})H(t-\frac{1}{2})+2g(t-1)H(t-1)</math> | ||
| + | |||
| + | את התמרת הלפלס של g קל לחשב: | ||
| + | |||
| + | <math>\mathcal{L} \{g(t)\}=\mathcal{L} \{t \}=\mathcal{L} \{t \cdot 1 \}=-\frac{d}{ds} \mathcal{L} \{ 1 \}=-\frac{d}{ds} \frac{1}{s}=- \left(-\frac{1}{s^2} \right)=\frac{1}{s^2}=G(s)</math> | ||
| + | |||
| + | (השתמשתי בתכונה מהשיעור: <math>\mathcal{L} \{ t \cdot (t) \}=-\frac{d}{ds} \mathcal{L} \{ f(t) \}</math>) | ||
| + | |||
| + | נפעיל כעת התמרת לפלס על המד"ר שלנו: | ||
| + | |||
| + | <math>\mathcal{L} \{y''\}=\mathcal{L} \{f \}</math> | ||
| + | |||
| + | <math>s^2Y(s)-sy(0)-y'(0)=\mathcal{L} \{ 2g(t)H(t)-4g(t-\frac{1}{2})H(t-\frac{1}{2})+2g(t-1)H(t-1) \}</math> | ||
| + | |||
| + | ע"פ תנאי ההתחלה אגף שמאל הוא בדיוק <math>s^2Y(s)</math>. כדי לחשב את אגף ימין נשתמש בלינאריות של התמרת לפלס, וניזכר בתכונה: | ||
| + | |||
| + | <math>\mathcal{L} \{g(t-c) \cdot H(t-c)\}=e^{-cs} G(s)</math> | ||
| + | |||
| + | המשוואה היא: | ||
| + | |||
| + | <math>s^2Y(s)=2\mathcal{L} \{g(t) H(t) \}-4\mathcal{L} \{g(t-\frac{1}{2}) H(t-\frac{1}{2}) \}+2 \mathcal{L} \{g(t-1) H(t-1) \}</math> | ||
| + | |||
| + | <math>s^2 Y(s)=2 e^{-0 s}G(s)-4 e^{-\frac{1}{2} s} G(s)+2 e^{-1 s} G(s)</math> | ||
| + | |||
| + | <math>s^2 Y(s)=(2-4 e^{-\frac{1}{2} s}+2 e^{-s}) G(s)</math> | ||
| + | |||
| + | <math>s^2 Y(s)=(2-4 e^{-\frac{1}{2} s}+2 e^{-s}) \frac{1}{s^2}</math> | ||
| + | |||
| + | <math>Y(s)=(2-4 e^{-\frac{1}{2} s}+2 e^{-s}) \frac{1}{s^4}</math> | ||
| + | |||
| + | <math>Y(s)=2\frac{1}{s^4}-4 e^{-\frac{1}{2} s}\frac{1}{s^4}+2 e^{-s}\frac{1}{s^4}</math> | ||
| + | |||
| + | נפעיל התמרת לפלס הפוכה כדי לקבל את הפתרון: | ||
| + | |||
| + | <math>y(t)=\mathcal{L}^{-1} \left\{ 2\frac{1}{s^4}-4 e^{-\frac{1}{2} s}\frac{1}{s^4}+2 e^{-s}\frac{1}{s^4} \right\}</math> | ||
| + | |||
| + | ע"פ לינאריות ההתמרה ההפוכה: | ||
| + | |||
| + | <math>y(t)=2\mathcal{L}^{-1} \left\{ \frac{1}{s^4} \right\}-4\mathcal{L}^{-1} \left\{ e^{-\frac{1}{2} s} \frac{1}{s^4} \right\}+2\mathcal{L}^{-1} \left\{ e^{-s} \frac{1}{s^4} \right\}</math> | ||
| + | |||
| + | לפי טבלת התמרת לפלס: | ||
| + | |||
| + | <math>\mathcal{L}^{-1} \left\{ \frac{1}{s^4} \right\}=\frac{t^3}{3!}=\frac{t^3}{6}</math> | ||
| + | |||
| + | אם כן: | ||
| + | |||
| + | <math>y(t)=2\frac{t^3}{6}-4 \frac{(t-\frac{1}{2})^3}{6}H \left(t-\frac{1}{2} \right)+2 \frac{(t-1)^3}{6} H(t-1)</math> | ||
| + | |||
| + | וזהו הפתרון. ניתן לבדוק שהוא רציף וגזיר אפילו בנקודה הבעייתית <math>t=\frac{1}{2}</math> | ||
| + | |||
| + | --[[משתמש:Michael|Michael]] 23:27, 31 בינואר 2012 (IST) | ||
גרסה אחרונה מ־18:28, 22 בפברואר 2012
88-240 משוואות דיפרנציאליות רגילות
קישורים
קובץ הסבר על שיטת המשמיד (באנגלית)
טבלה של התמרות לפלס - יש גם דברים שלא למדנו
הודעות
חשוב: תאריך ההגשה של תרגיל 8 הוא עד יום ראשון הקרוב בשעה 12:00 לתא של פרופ' שיף (113) --Michael 18:02, 4 בינואר 2012 (IST)
העלתי קובץ ובו פתרון של בעיית שפה לפי שיטת גרין. שימו לב שמדובר כאן על תנאי שפה מסויימים, נא לא להתבלבל. --Michael 20:24, 27 בנובמבר 2011 (IST)
העלתי את פתרון תרגיל 11 ואת ציוני התרגילים. מי שמוצא טעות נא להודיע לי --Michael 20:28, 22 בפברואר 2012 (IST)
לגבי התרגול היום (6.12.2011):
הגענו לפתרון 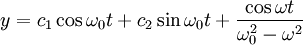
ומשם בלי ממש להסביר איך, שינינו קצת את 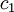 כדי שהגבול יתכנס.
הדרך המלאה היא כך:
כדי שהגבול יתכנס.
הדרך המלאה היא כך:
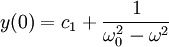
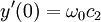
(לא קשה לראות שזה נכון). אפשר לבודד את הקבועים:
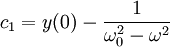
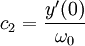
ולכן הפתרון הוא:
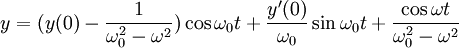
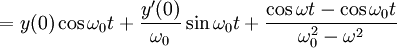
עכשיו נוכל להשאיף 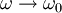 ולקבל (תוך כדי שימוש בכלל לופיטל):
ולקבל (תוך כדי שימוש בכלל לופיטל):
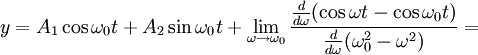
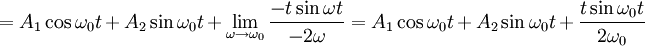
כאשר:
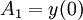 ו-
ו- 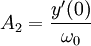 הם קבועים חופשיים.
הם קבועים חופשיים.
רצוי מאוד שתשתמשו בדרך המלאה הזו, ולא בדרך הקצרה יותר שלמדנו היום. --Michael 22:53, 6 בדצמבר 2011 (IST)
בתרגול היום דיברנו על מערכות הומוגניות עם מקדמים קבועים:
הדבר הראשון שצריכים לעשות הוא למצוא ע"ע.
למקרה שתתקלו במד"ר בספרות, כדאי שתדעו את השמות של המקרים שנתקלנו בהם.
המקרה הראשון היה ע"ע פשוט ממשי - simple real eigenvalue
המקרה השני היה זוג ע"ע מרוכבים פשוטים - simple complex conjugate pair eigenvalues
המקרה השלישי היה ע"ע מריבוי אלגברי גבוה m שבכל זאת (למזלנו) ניתן למצוא לו m וקטורים עצמיים. לע"ע שכזה קוראים ע"ע שלם - complete eigenvalue
והמקרה הכי פחות קל, ע"ע מריבוי גבוה m שיש לו פחות מ-m ו"ע. ע"ע כזה נקרא ע"ע דפקטיבי - defective eigenvalue
פתרון יותר מפורט של המקרה האחרון:
רצינו לפתור את המד"ר
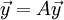 , כאשר
, כאשר 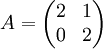
ל-A יש רק ע"ע אחד 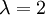 . נחפש ו"ע
. נחפש ו"ע 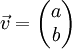 :
:
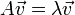
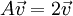
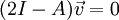
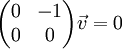
מקבלים את התנאי 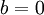 וניתן לקחת
וניתן לקחת 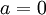 ולקבל ו"ע
ולקבל ו"ע 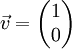 ולכן את הפתרון הקלאסי :
ולכן את הפתרון הקלאסי :
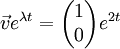
נראה שאין תקווה כי אי אפשר לבנות עוד פתרון כזה. אבל צריכים לחפש פתרון מהצורה 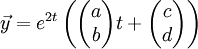 .
.
מצד אחד:
![\vec{y}'=\left[e^{2t} \begin{pmatrix} at+c\\bt+d \end{pmatrix}\right] '=2e^{2t}\begin{pmatrix} at+c\\bt+d \end{pmatrix}+e^{2t}\begin{pmatrix} a\\b \end{pmatrix}=e^{2t}\begin{pmatrix} 2at+2c+a\\2bt+2d+b \end{pmatrix}](/images/math/b/b/d/bbd00cd9f2213bf29bea7c7e059f673a.png)
ומצד שני:
![A \vec{y}=\begin{pmatrix} 2 & 1\\ 0&2 \end{pmatrix}\left[ e^{2t} \begin{pmatrix} at+c\\bt+d \end{pmatrix}\right]=e^{2t} \begin{pmatrix} 2at+2c+bt+d\\ 2bt+2d\end{pmatrix}](/images/math/0/c/8/0c88b5c854b3d20cd14ca50f79b600db.png)
כדי לקבל שוויון ביניהם, נצטרך:
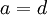
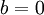
(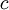 נשאר חופשי)
נשאר חופשי)
נציב זאת בניחוש ונקבל:
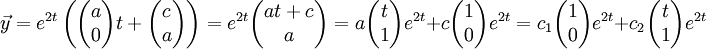
בתרגול לקחתי c=0 ו-a=1 ובניתי פתרון נוסף שבכל מקרה הצטרף לפתרון הראשוני. סליחה על הבלבול.
--Michael 21:50, 22 בדצמבר 2011 (IST)
למרות שראיתם בהרצאה דוגמה לפתרון מערכת לא הומוגנית אני חושב שכדאי שאפתור עוד אחת כאן. נניח שרוצים לפתור את:
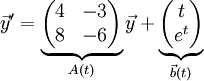
הדבר הראשון שצריכים לעשות הוא למצוא מטריצה יסודית כלשהי, בתרגול ראינו למשל את המטריצה:
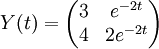
השלב הבא הוא לחשב את המטריצה ההופכית, המחשב נתן לי:
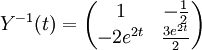
נחשב עכשיו את 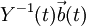 :
:
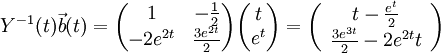
ניקח אינטגרל (אינטגרל של וקטור עושים רכיב-רכיב):
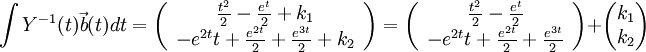
כל מה שנותר לעשות הוא להכפיל במטריצה יסודית:
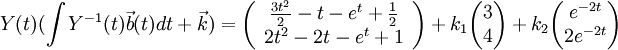
זהו בדיוק הפתרון הכללי של המערכת 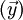 . אם היה נתון תנאי התחלה היינו צריכים למצוא את הקבועים החופשיים.
--Michael 01:49, 27 בדצמבר 2011 (IST)
. אם היה נתון תנאי התחלה היינו צריכים למצוא את הקבועים החופשיים.
--Michael 01:49, 27 בדצמבר 2011 (IST)
לגבי סוף התרגול היום: עסקנו במשוואה 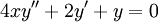 . המשוואה האינדנציאלית נתנה לנו שני ערכים מותרים עבור
. המשוואה האינדנציאלית נתנה לנו שני ערכים מותרים עבור 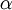 :
: 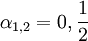 הגענו לפתרון אחד כאשר לקחנו
הגענו לפתרון אחד כאשר לקחנו 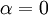 :
:
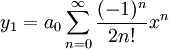 אמרנו שאם מדובר בתחום שבו x>0 ניתן לרשום אותו בצורה:
אמרנו שאם מדובר בתחום שבו x>0 ניתן לרשום אותו בצורה:
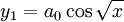 נגיע עכשי לפתרון השני, ניקח הפעם את
נגיע עכשי לפתרון השני, ניקח הפעם את 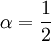 . הרקורסיה שלנו היא
. הרקורסיה שלנו היא
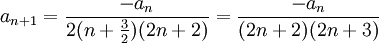
נמצא קצת מהמקדמים:
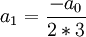
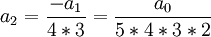
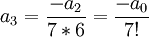
כבר ניתן לנחש:
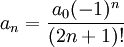
אם כך, נקבל פתרון שני:
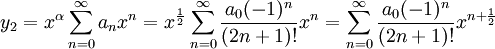
אם x חיובי נוכל לרשום אותו בצורה:
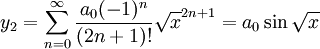
הפתרון הכללי יהיה צירוף לינארי שלהם:
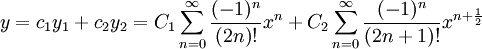
כאשר הקבועים הגדולים בלעו את 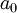
הערה חשובה: שימו לב שלא תמיד ניתן לפתור את הרקורסיות (אפילו לא במונחים של פונקציית גמא). במקרה כזה רצוי שלפחות תפתחו את הטור לכמה איברים ראשונים.
--Michael 01:37, 3 בינואר 2012 (IST)
הנה דוגמא של מד"ר, כאשר אגף ימין הוא מוגדר למקוטעין:
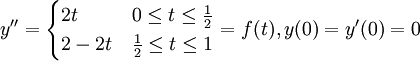
"כזכור", ניתן לרשום פונקצייה מוגדרת למקוטעין בעזרת פונקציית הביסייד עם שני פרמטרים כך:
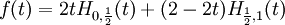
(האמת שיש כאן קצת בלוף: יש בעיה בנקודות ה"תפירה" 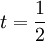 . לא אמרנו מה קורה לפונקציית הביסייד באפס. אבל בכל מקרה, להתמרת לפלס לא ממש אכפת מה קורה בנקודה בודדת)
. לא אמרנו מה קורה לפונקציית הביסייד באפס. אבל בכל מקרה, להתמרת לפלס לא ממש אכפת מה קורה בנקודה בודדת)
נפשט קצת את 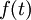 :
:
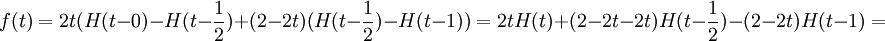
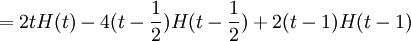
נגדיר פונקצייה נוספת לנוחיותנו:
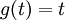
ואז ניתן לרשום:
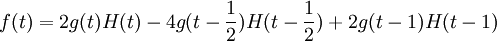
את התמרת הלפלס של g קל לחשב:
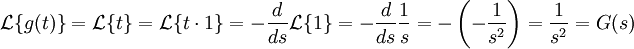
(השתמשתי בתכונה מהשיעור: 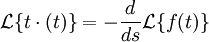 )
)
נפעיל כעת התמרת לפלס על המד"ר שלנו:
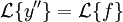
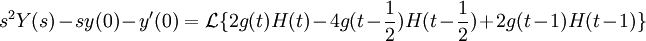
ע"פ תנאי ההתחלה אגף שמאל הוא בדיוק 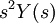 . כדי לחשב את אגף ימין נשתמש בלינאריות של התמרת לפלס, וניזכר בתכונה:
. כדי לחשב את אגף ימין נשתמש בלינאריות של התמרת לפלס, וניזכר בתכונה:
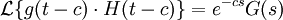
המשוואה היא:
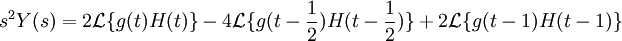
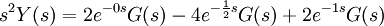
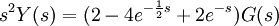
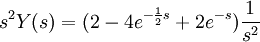
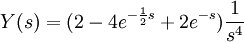
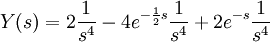
נפעיל התמרת לפלס הפוכה כדי לקבל את הפתרון:
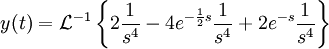
ע"פ לינאריות ההתמרה ההפוכה:
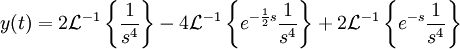
לפי טבלת התמרת לפלס:
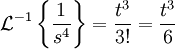
אם כן:
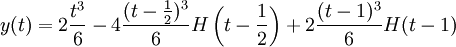
וזהו הפתרון. ניתן לבדוק שהוא רציף וגזיר אפילו בנקודה הבעייתית 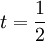
--Michael 23:27, 31 בינואר 2012 (IST)