88-240 משוואות דיפרנציאליות רגילות סמסטר א תשעב
88-240 משוואות דיפרנציאליות רגילות
קישורים
קובץ הסבר על שיטת המשמיד (באנגלית)
הודעות
העלתי קובץ ובו פתרון של בעיית שפה לפי שיטת גרין. שימו לב שמדובר כאן על תנאי שפה מסויימים, נא לא להתבלבל. --Michael 20:24, 27 בנובמבר 2011 (IST)
לגבי התרגול היום (6.12.2011):
הגענו לפתרון 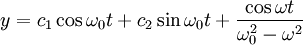
ומשם בלי ממש להסביר איך, שינינו קצת את 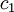 כדי שהגבול יתכנס.
הדרך המלאה היא כך:
כדי שהגבול יתכנס.
הדרך המלאה היא כך:
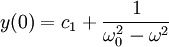
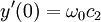
(לא קשה לראות שזה נכון). אפשר לבודד את הקבועים:
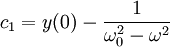
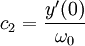
ולכן הפתרון הוא:
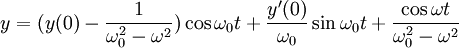
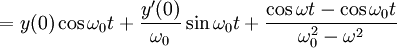
עכשיו נוכל להשאיף 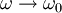 ולקבל (תוך כדי שימוש בכלל לופיטל):
ולקבל (תוך כדי שימוש בכלל לופיטל):
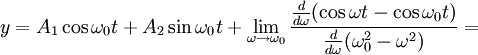
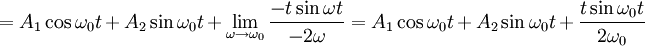
כאשר:
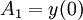 ו-
ו- 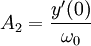 הם קבועים חופשיים.
הם קבועים חופשיים.
רצוי מאוד שתשתמשו בדרך המלאה הזו, ולא בדרך הקצרה יותר שלמדנו היום. --Michael 22:53, 6 בדצמבר 2011 (IST)
בתרגול היום דיברנו על מערכות הומוגניות עם מקדמים קבועים:
הדבר הראשון שצריכים לעשות הוא למצוא ע"ע.
למקרה שתתקלו במד"ר בספרות, כדאי שתדעו את השמות של המקרים שנתקלנו בהם.
המקרה הראשון היה ע"ע פשוט ממשי - simple real eigenvalue
המקרה השני היה זוג ע"ע מרוכבים פשוטים - simple complex conjugate pair eigenvalues
המקרה השלישי היה ע"ע מריבוי אלגברי גבוה m שבכל זאת (למזלנו) ניתן למצוא לו m וקטורים עצמיים. לע"ע שכזה קוראים ע"ע שלם - complete eigenvalue
והמקרה הכי פחות קל, ע"ע מריבוי גבוה m שיש לו פחות מ-m ו"ע. ע"ע כזה נקרא ע"ע דפקטיבי - defective eigenvalue
פתרון יותר מפורט של המקרה האחרון:
רצינו לפתור את המד"ר
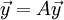 , כאשר
, כאשר 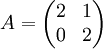
ל-A יש רק ע"ע אחד 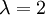 . נחפש ו"ע
. נחפש ו"ע 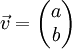 :
:
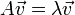
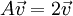
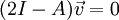
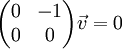
מקבלים את התנאי 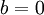 וניתן לקחת
וניתן לקחת 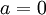 ולקבל ו"ע
ולקבל ו"ע 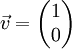 ולכן את הפתרון הקלאסי :
ולכן את הפתרון הקלאסי :
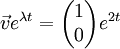
נראה שאין תקווה כי אי אפשר לבנות עוד פתרון כזה. אבל צריכים לחפש פתרון מהצורה 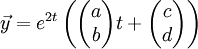 .
.
מצד אחד:
![\vec{y}'=\left[e^{2t} \begin{pmatrix} at+c\\bt+d \end{pmatrix}\right] '=2e^{2t}\begin{pmatrix} at+c\\bt+d \end{pmatrix}+e^{2t}\begin{pmatrix} a\\b \end{pmatrix}=e^{2t}\begin{pmatrix} 2at+2c+a\\2bt+2d+b \end{pmatrix}](/images/math/b/b/d/bbd00cd9f2213bf29bea7c7e059f673a.png)
ומצד שני:
![A \vec{y}=\begin{pmatrix} 2 & 1\\ 0&2 \end{pmatrix}\left[ e^{2t} \begin{pmatrix} at+c\\bt+d \end{pmatrix}\right]=e^{2t} \begin{pmatrix} 2at+2c+bt+d\\ 2bt+2d\end{pmatrix}](/images/math/0/c/8/0c88b5c854b3d20cd14ca50f79b600db.png)
כדי לקבל שוויון ביניהם, נצטרך:
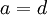
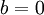
(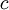 נשאר חופשי)
נשאר חופשי)
נציב זאת בניחוש ונקבל:
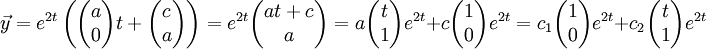
בתרגול לקחתי c=0 ו-a=1 ובניתי פתרון נוסף שבכל מקרה הצטרף לפתרון הראשוני. סליחה על הבלבול.
--Michael 21:50, 22 בדצמבר 2011 (IST)
למרות שראיתם בהרצאה דוגמה לפתרון מערכת לא הומוגנית אני חושב שכדאי שאפתור עוד אחת כאן. נניח שרוצים לפתור את:
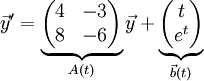
הדבר הראשון שצריכים לעשות הוא למצוא מטריצה יסודית כלשהי, בתרגול ראינו למשל את המטריצה:
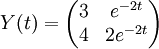
השלב הבא הוא לחשב את המטריצה ההופכית, המחשב נתן לי:
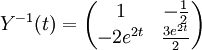
נחשב עכשיו את 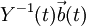 :
:
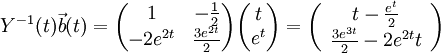
ניקח אינטגרל (אינטגרל של וקטור עושים רכיב-רכיב):
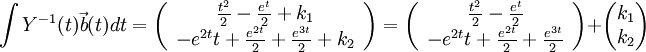
כל מה שנותר לעשות הוא להכפיל במטריצה יסודית:
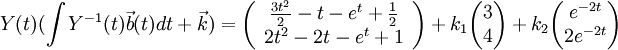
זהו בדיוק הפתרון הכללי של המערכת 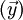 . אם היה נתון תנאי התחלה היינו צריכים למצוא את הקבועים החופשיים.
--Michael 01:49, 27 בדצמבר 2011 (IST)
. אם היה נתון תנאי התחלה היינו צריכים למצוא את הקבועים החופשיים.
--Michael 01:49, 27 בדצמבר 2011 (IST)
לגבי סוף התרגול היום: עסקנו במשוואה 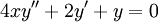 . המשוואה האינדנציאלית נתנה לנו שני ערכים מותרים עבור
. המשוואה האינדנציאלית נתנה לנו שני ערכים מותרים עבור 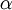 :
: 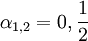 הגענו לפתרון אחד כאשר לקחנו
הגענו לפתרון אחד כאשר לקחנו 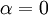 :
:
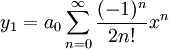 אמרנו שאם מדובר בתחום שבו x>0 ניתן לרשום אותו בצורה:
אמרנו שאם מדובר בתחום שבו x>0 ניתן לרשום אותו בצורה:
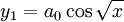 נגיע עכשי לפתרון השני, ניקח הפעם את
נגיע עכשי לפתרון השני, ניקח הפעם את 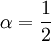 . הרקורסיה שלנו היא
. הרקורסיה שלנו היא
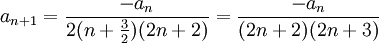
נמצא קצת מהמקדמים:
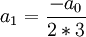
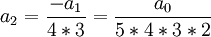
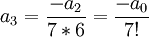
כבר ניתן לנחש:
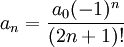
אם כך, נקבל פתרון שני:
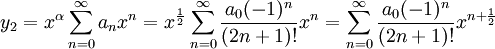
אם x חיובי נוכל לרשום אותו בצורה:
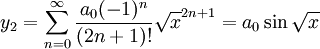
הפתרון הכללי יהיה צירוף לינארי שלהם:
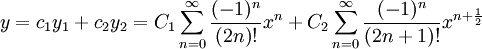
כאשר הקבועים הגדולים בלעו את 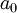
הערה חשובה: שימו לב שלא תמיד ניתן לפתור את הרקורסיות (אפילו לא במונחים של פונקציית גמא). במקרה כזה רצוי שלפחות תפתחו את הטור לכמה איברים ראשונים.
--Michael 01:37, 3 בינואר 2012 (IST)