אורך עקומה
מתוך Math-Wiki
תהי  פונקציה גזירה ברציפות בקטע סגור
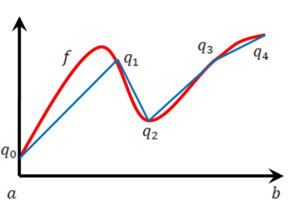
פונקציה גזירה ברציפות בקטע סגור ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) . נקרב את אורך העקומה שלה (אורך הקו שלה בגרף) על-ידי גבול סכום המיתרים בין נקודות הפונקציה על חלוקות (סכום הקווים הכחולים בציור).
. נקרב את אורך העקומה שלה (אורך הקו שלה בגרף) על-ידי גבול סכום המיתרים בין נקודות הפונקציה על חלוקות (סכום הקווים הכחולים בציור).
עבור חלוקת הקטע 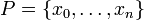 , הנוסחא לסכום המיתרים נתונה על-ידי:
, הנוסחא לסכום המיתרים נתונה על-ידי:
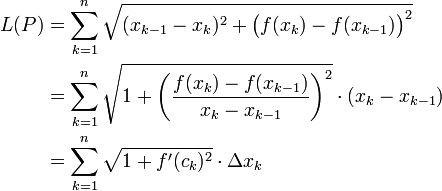
כאשר הנקודות 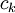 מקיימות
מקיימות 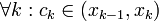 . אכן קיימות נקודות כאלה לפי משפט לגראנז'.
. אכן קיימות נקודות כאלה לפי משפט לגראנז'.
הגענו לסכום רימאן עבור הפונקציה 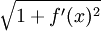 . כיון שנתון כי
. כיון שנתון כי 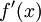 רציפה, גם
רציפה, גם 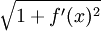 רציפה בקטע הסגור ולכן אינטגרבילית.
רציפה בקטע הסגור ולכן אינטגרבילית.
על כן סכומי רימאן אלה שואפים לאינטגרל 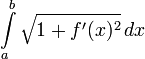 וזוהי הנוסחא לחישוב אורך עקום של פונקציה.
וזוהי הנוסחא לחישוב אורך עקום של פונקציה.