אנליזה מתקדמת למורים תרגול 5

חזרה ל מערכי תרגול.

הגדרה

נאמר שפונקציה גזירה בנקד' 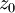$z_0$ אם לכל סדרה 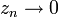$z_n\to 0$ קיים הגבול 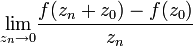$\underset{z_n\to 0}{\lim}\frac{f(z_n+z_0)-f(z_0)}{z_n}$, ואז ערך הנגזרת זה הגבול הנ"ל.

פונקציה היא גזירה אם היא גזירה בכל נקודה.

דוגמאות

תרגיל

האם הפונקציה 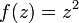$f(z)=z^2$ גזירה?

פתרון

כן. לפי הגדרה, מקבלים בדיוק כמו בממשיים!

תרגיל

האם הפונקציה 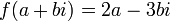$f(a+bi)=2a-3bi$ גזירה?

פתרון

לא! לוקחים סדרה ממשית וסדרה מדומה טהורה.

משפטים

סכום ומכפלה של גזירות גזירה. כלל השרשת גם מתקיים!

תרגיל

א. תהי 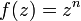$f(z)=z^n$ הוכיחו: $f'(z)=nz^{n-1}$.

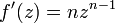ב. יהי 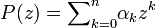$P(z)={\sum}_{k=0}^{n} \alpha_kz^k$ פולינום. הוכיחו ש- $P'(z)={\sum}_{k=1}^{n} k\alpha_kz^{k-1}$.

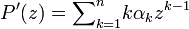פתרון

א. באינדוקציה ע"י כלל המכפלה.

ב. מסעיף קודם וכלל החיבור.

תנאי קושי-רימן

נגזרות חלקיות

תהי 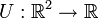$U:\mathbb{R}^2\to \mathbb{R}$ פונקציה, אזי הנגזרת החלקית לפי אחד המשתנים, זה לגזור כאילו זה המשתנה והמשתנה השני קבוע.

דוגמא: 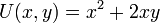$U(x,y)=x^2+2xy$ אז הנגזרות החלקיות הן: $U_x=2x+2y,U_y=2x$.

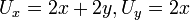עוד דוגמא כרוח המתרגל באותה שעה.

כעת נראה קריטריון לגזירות פונקציה, ע"י הנגזרות החלקיות של 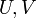$U,V$ המתאימות.

תנאי קושי רימן

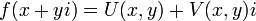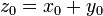תהי $f(x+yi)=U(x,y)+V(x,y)i$ פונקציה מרוכבת. $f$ גזירה בנקודה $z_0=x_0+y_0$ אם ורק אם הנגזרות החלקיות קיימות ומקיימות את המשוואות הבאות:

$\begin{cases} U_x=V_y \\ U_y=-V_x \end{cases}$.

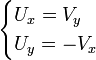ובמקרה זה מתקיים: 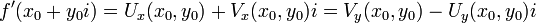$f'(x_0+y_0i)=U_x(x_0,y_0)+V_x(x_0,y_0)i=V_y(x_0,y_0)-U_y(x_0,y_0)i$.

תרגיל

בדקו באילו נקודות הפונקציות הבאות גזירות, ומצאו את הנגזרת בנקודות אלו:

1. $f(x+yi)=e^x\text{cis}y$

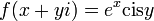
2. $f(z)=z+Re(z)$

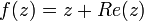
3. $f(z)=(z-1)(Re(z))^2$

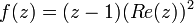
4. $f(x+yi)=x+y^3i$

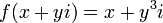
פתרון

1. נקבל: 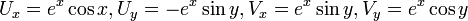$U_x=e^x\cos x,U_y=-e^x\sin y,V_x=e^x\sin y,V_y=e^x\cos y$. ואכן מתקיים תנאי קושי-רימן בכל נקודה. לכן זו פונקציה גזירה בכל נקודה שנגזרתה: 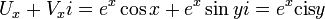$U_x+V_xi=e^x\cos x+e^x\sin yi=e^x\text{cis}y$. שימו לב מה קיבלנו - הנגזרת שלה זה היא בעצמה!!

2. לא גזירה באף נקודה כי נקבל 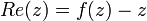$Re(z)=f(z)-z$, ואם היא גזירה בנקודה אז גם פונקציית החלק הממשי גזירה שם, כהפרש גזירות, בסתירה לכך שהיא לא גזירה באף נקודה.

3. נרשום: 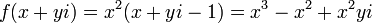$f(x+yi)=x^2(x+yi-1)=x^3-x^2+x^2yi$. נמצא נגזרות חלקיות: 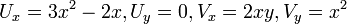$U_x=3x^2-2x,U_y=0,V_x=2xy,V_y=x^2$. נבדוק מתי התנאי מתקיים:

$U_x=V_y\iff 3x^2-2x=x^2\iff x(x-2)=0\iff x=0\lor x=2$.

$U_y=-V_x\iff 0=-2xy\iff x=0\lor y=0$.

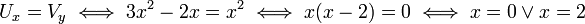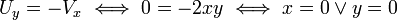שני התנאים מתקיים כאשר: 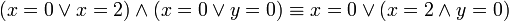$(x=0\lor x=2)\land (x=0\lor y=0)\equiv x=0\lor (x=2\land y=0)$. כלומר גזירה בציר המדומה, ובנקודה $(2,0)$.

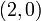הנגזרת שם היא: 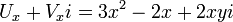$U_x+V_xi=3x^2-2x+2xyi$. נשים לב שעל הציר המדומה 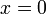$x=0$ ולכן הנגזרת היא אפס. בנקודה 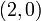$(2,0)$ נקבל $f'(2)=3\cdot 2^2-2\cdot 2=8$.

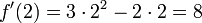4. נקבל את הנגזרות החלקיות: 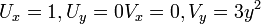$U_x=1,U_y=0V_x=0,V_y=3y^2$. נבדוק את התנאי:

$U_x=V_y\iff 1=3y^2\iff y^2=\frac{1}{3}\iff y=\pm\frac{1}{\sqrt{3}}$.

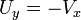$U_y=-V_x$ תמיד.

לכן רק בנקודות 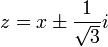$z=x\pm\frac{1}{\sqrt{3}}i$ הפונקציה גזירה, ונגזרתה שם: $U_x+V_xi=1$.

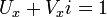משפט

פונקציה גזירה שנגזרתה אפס על כל הממשיים היא פונקציה קבועה.

תרגיל

הוכיחו שאם 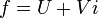$f=U+Vi$ גזירה והחלק הממשי של $f$ הוא פונקציה קבועה אז $f$ קבועה.

פתרון

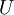$U$ קבועה ולכן 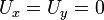$U_x=U_y=0$, וכיון שהפונקציה גזירה נובע שמתקיימות משוואות קושי-רימן, ולכן 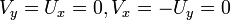$V_y=U_x=0,V_x=-U_y=0$, ולכן גם $V$ קבועה. ולכן$f$ קבועה.