מדר קיץ תשעב/סיכומים/תרגולים/1.8.12
טרם נערך
………
תוכן עניינים
דוגמה
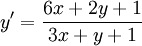
פתרון
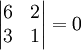
לכן 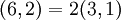 ונסמן
ונסמן 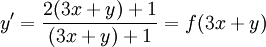 . נציב
. נציב 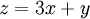 ונגזור לפי
ונגזור לפי  :
: 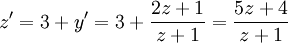 .
.
נבדוק 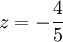 ונקבל שזה פיתרון. עתה נניח ש־
ונקבל שזה פיתרון. עתה נניח ש־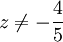 ולכן
ולכן
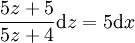 .
.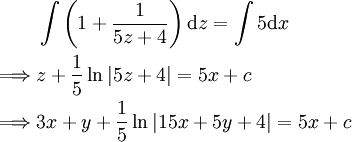
ו־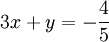 פתרון סינגולרי בצורת קו ישר.
פתרון סינגולרי בצורת קו ישר.
מקרה 2
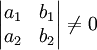 . במקרה זה נציב
. במקרה זה נציב 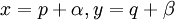 . נבחר את
. נבחר את 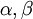 כך שיאפסו את המחוברים הקבועים במונה ובמכנה, וכך נגיע למד״ר הומוגנית עבור
כך שיאפסו את המחוברים הקבועים במונה ובמכנה, וכך נגיע למד״ר הומוגנית עבור 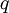 כפונקציה של
כפונקציה של 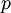 .
.
דוגמה
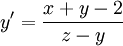 . אזי
. אזי 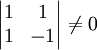 ונציב באופן הנ״ל. מתקיים
ונציב באופן הנ״ל. מתקיים 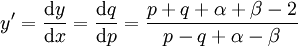 . נרצה ש־
. נרצה ש־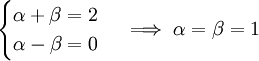 . לפיכך
. לפיכך 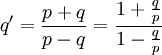 ונסמן
ונסמן 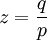 .לפיכך
.לפיכך 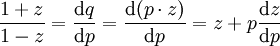 . נקבל
. נקבל 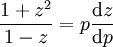 ומכאן ש־
ומכאן ש־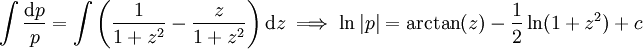 . לבסוף,
. לבסוף, 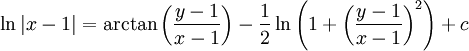 .
.
מד״ר לינאריות מסדר ראשון
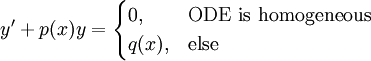 . אם המד״ר הומוגנית ניתן להפריד משתנים ולהגיע לפתרון
. אם המד״ר הומוגנית ניתן להפריד משתנים ולהגיע לפתרון 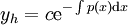 . כדי לפתור מד״ר אי־הומוגנית קודם כל פותרים את המד״ר ההומוגנית המתאימה (בודקים
. כדי לפתור מד״ר אי־הומוגנית קודם כל פותרים את המד״ר ההומוגנית המתאימה (בודקים 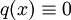 ) ואז מציבים
) ואז מציבים 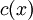 במקום
במקום 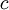 . לסיום פותרים עבור הפונקציה
. לסיום פותרים עבור הפונקציה 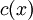 .
.
תרגיל
מצא את הפתרון הכללי של המד״ר 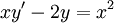 .
.
פתרון
נביא את המד״ר לצורה 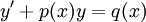 ע״י חילוק ב־
ע״י חילוק ב־ :
: 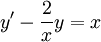 . לכן
. לכן 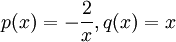 . המד״ר ההומוגנית המתאימה היא
. המד״ר ההומוגנית המתאימה היא 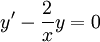 שפתרונה
שפתרונה 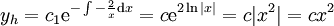 . נשתמש בווריאציית המקדמים ונצא פתרון מהצורה
. נשתמש בווריאציית המקדמים ונצא פתרון מהצורה 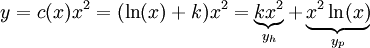 .
. 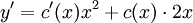 נציב במד״ר
נציב במד״ר 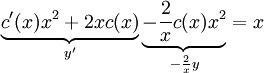 . עתה
. עתה 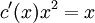 ולכן
ולכן 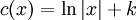 .
.
תרגיל
נתון מעגל חשמלי כמתואר בציור. לפי חוק קירכהוף הזרם במעגל, 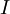 , מקיים את המשוואה הדיפרנציאלית
, מקיים את המשוואה הדיפרנציאלית 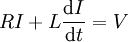 .
.
- בהנתן שבזמן
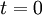 המעגל פתוח ומייד לאחר מכן סוגרים את המתג, מצא את הזרם החשמלי במעגל בזמן
המעגל פתוח ומייד לאחר מכן סוגרים את המתג, מצא את הזרם החשמלי במעגל בזמן 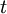 כלשהו.
כלשהו. - מהו הזרם החשמלי במעגל לאחר זמן רב,
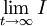 ?
?
פתרון
- כשהמעגל פתוח לא זורם בו זרם – משמע יש לנו תנאי התחלה
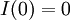 . המד״ר היא
. המד״ר היא 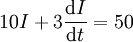 . נביא לצורה
. נביא לצורה 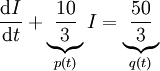 . עפ״י הנוסחה מההרצאה, הפתרון הכללי הוא
. עפ״י הנוסחה מההרצאה, הפתרון הכללי הוא 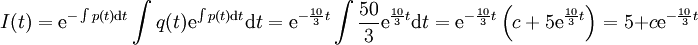
………
- כעבור זמן רב הזרם הוא
![\lim_{t\to\infty}I(t)=5(1-0)=5[A]](/images/math/8/d/4/8d47ad11dbfbc5e1174472478acb07a2.png) (Ampe`re).
(Ampe`re).
תרגיל
פתור 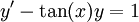 בקטע
בקטע 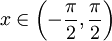 .
.
פתרון
זוהי מד״ר לינארית מסדר ראשון עם 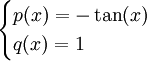 . ע״ס הנוסחה
. ע״ס הנוסחה 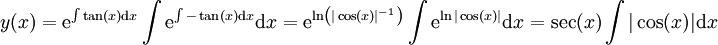 בקטע הנתון
בקטע הנתון 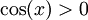 ולכן ניתן להתעלם מהערך המוחלט.
ולכן ניתן להתעלם מהערך המוחלט.
………
משוואת ברנולי
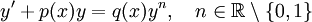 . ניתן להציב
. ניתן להציב 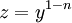 ולקבל מד״ר לינארית, או לחלופין להשתמש בנוסחה המפלצתית
ולקבל מד״ר לינארית, או לחלופין להשתמש בנוסחה המפלצתית ![y(x)=\sqrt[1-n]{\mathrm e^{-\int(1-n)p(x)\mathrm dx}\int(1-n)q(x)\mathrm e^{\int(1-n)p(x)\mathrm dx}\mathrm dx}](/images/math/d/5/3/d53e6fe6c5c49618a6a6fbf734fea332.png)
………
מד״ר מדויקת
מד״ר מהצורה 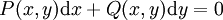 נקראת מדוייקת בתחום
נקראת מדוייקת בתחום 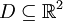 אם קיימת פוקנציה סקלרית
אם קיימת פוקנציה סקלרית 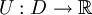 כך ש־
כך ש־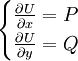 . אם כן המד״ר היא
. אם כן המד״ר היא 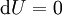 ופתרונותיה
ופתרונותיה 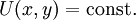 הן עקומות הרמה של
הן עקומות הרמה של 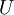 . תנאי הכרחי הוא
. תנאי הכרחי הוא 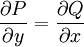 .
.
תרגיל
פתור את המד״ר 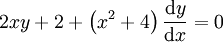 .
.
פתרון
נכפיל ב־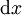 ונקבל
ונקבל 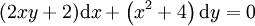 ונחפש פונקצית דיפרנציאל
ונחפש פונקצית דיפרנציאל 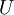 כנ״ל.
כנ״ל.
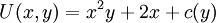 .
.
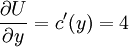
………
ואם המד״ר לא מדוייקת? נכפיל פי 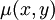 ונגרוש ש־
ונגרוש ש־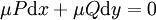 מדוייקת. כדי ש־
מדוייקת. כדי ש־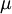 תהא תלויה ב־
תהא תלויה ב־ בלבד צריך להתקיים
בלבד צריך להתקיים 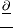
…………
תרגיל
פתרו 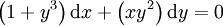 . אזי
. אזי 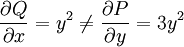 . ולכן המד״ר אינה מדויקת. אבל
. ולכן המד״ר אינה מדויקת. אבל 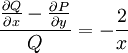 , כלומר התלות ב־
, כלומר התלות ב־ בלבד, כדרוש.
בלבד, כדרוש.