מכינה למתמטיקה קיץ תשעב/תרגילים/8/פתרון 8
מתוך Math-Wiki
1
קבעו אילו מן המשפטים הבאים שקולים לשלילה של המשפט "לכל קוף ולכל קרנף, יש ג'ירפה שאם אביה שמן כמו הקרנף, אז אמה מכוערת כמו הקוף"
- יש קוף כך שלכל הג'ירפות אין אבא שמן כמו אף קרנף או שאימן יפה מהקוף
- לא שלילה. קוף אחד, קרנף אחד, ג'ירפה אחת. האב של הג'ירפה רזה מהקרנף
- יש קוף, קרנף וג'ירפה עם אבא ששמן כמו הקרנף ואמא שיפה מהקוף
- לא שלילה. קוף אחד, קרנף אחד, שתי ג'ירפות. האב של הג'ירפה הראשונה רזה מהקרנף. לג'ירפה השנייה יש אבא ששמן כמו הקרנף ואמא שיפה מהקוף
- לכל קוף אין קרנף כך שיש ג'ירפה שאם אביה שמן כמו הקרנף, אז אמה מכוערת כמו הקוף
- לא שלילה. קוף אחד, שני קרנפים, ג'ירפה אחת. האמא של הג'ירפה יפה מהקוף. אביה של הג'ירפה שמן כמו הקרנף הראשון, ורזה מהקרנף השני.
- יש קוף וקרנף שלכל הג'ירפות שאין להן אבא שמן כמו הקרנף, אין להם אמא מכוערת כמו הקוף
- לא שלילה. קוף אחד, קרנף אחד, ג'ירפה אחת. האבא של הג'ירפה רזה מהקרנף, והאמא שלה יפה מהקוף.
- יש קוף וקרנף שלכל הג'ירפות שאביהן שמן כמו הקרנף, אימן יפה מן הקוף
- לא שלילה. קוף אחד, קרנף אחד, ג'ירפה אחת. האבא של הג'ירפה רזה מהקרנף.
- יש קוף וקרנף שלכל הג'ירפות או שאימן יפה מן הקוף או שאבא שלהן רזה מן הקרנף
- לא שלילה. קוף אחד, קרנף אחד, ג'ירפה אחת. האבא של הג'ירפה רזה מהקרנף, האמא שלה מכוערת כמו הקוף.
מצא דוגמא נגדית לכל אחד מן המשפטים שאינו שקול לשלילה.
2
הגדרה:
קבוצת וקטורים 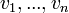 נקראת תלוייה לינארית אם קיימים סקלרים
נקראת תלוייה לינארית אם קיימים סקלרים 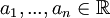 כך שלפחות אחד מהם שונה מאפס וגם
כך שלפחות אחד מהם שונה מאפס וגם 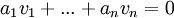
אילו מן ההגדרות הבאות מתאימה לקבוצת וקטורים שאינה תלוייה לינארית:
- וקטורים המקיימים
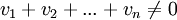
- לא, כי יתכן שקיים צירוף לינארי לא טריוויאלי אחר של הוקטורים שכן מתאפס
- וקטורים המקיימים
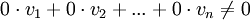
- לא, אף קבוצת וקטורים לא מקיימת הגדרה זו (למרות שכן יש קבוצות וקטורים שאינן תלויות לינארית)
- וקטורים המקיימים את התנאי- אם
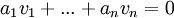 אזי
אזי 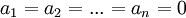
- כן, כי אם הקבוצה הייתה תלויה לינארית אז היו קיימים סקלרים
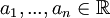 כך שלפחות אחד מהם שונה מאפס וגם
כך שלפחות אחד מהם שונה מאפס וגם 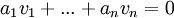 , אבל אז כולם היו שווים לאפס לפי ההגדרה בסתירה.
, אבל אז כולם היו שווים לאפס לפי ההגדרה בסתירה.
- כן, כי אם הקבוצה הייתה תלויה לינארית אז היו קיימים סקלרים
- וקטורים שלעולם לא מקיימים את התנאי
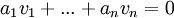
- לא, מכיוון שקבוצת וקטורים שאינה תלויה לינארית יכולה לקיים את התנאי עבור
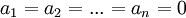
- לא, מכיוון שקבוצת וקטורים שאינה תלויה לינארית יכולה לקיים את התנאי עבור
3
תהיינה A,B,C קבוצות. נניח נתון 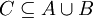 .
.
הוכח/הפרך כל אחת מן הטענות הבאות:
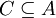 או
או 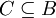
- הפרכה:
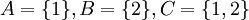
- הפרכה:
- אם
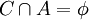 אזי
אזי 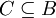
- הוכחה: יהי
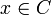 . לכן
. לכן 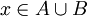 לכן
לכן 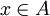 או
או 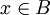 . נתון
. נתון 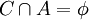 לכן
לכן 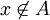 לכן
לכן 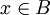
- הוכחה: יהי
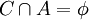 אם ורק אם
אם ורק אם 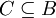
- הפרכה:
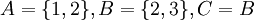
- הפרכה:
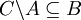
- הוכחה: יהי
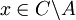 . לכן
. לכן 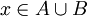 לכן
לכן 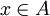 או
או 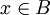 . לפי הגדרת x הוא לא בA לכן הוא בB.
. לפי הגדרת x הוא לא בA לכן הוא בB.
- הוכחה: יהי
- אם
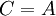 אזי
אזי 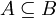
- הפרכה:
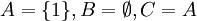
- הפרכה:
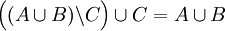
- הוכחה. היעזרו במשפטים הבאים (אחרי שתוכיחו אותם):
1. אם 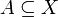 וגם
וגם 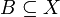 אז
אז 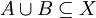
2. 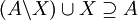
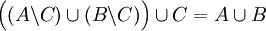
- הוכחה:
אגף שמאל הוא איחוד של שלוש קבוצות המוכלות ב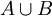 לכן כל אגף שמאל מוכל באגף ימין
יהי
לכן כל אגף שמאל מוכל באגף ימין
יהי 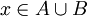 . אם
. אם 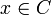 אז הוא באגף שמאל בגלל האיחוד עם C. אחרת,
אז הוא באגף שמאל בגלל האיחוד עם C. אחרת, 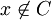 . לפי ההגדרה של x הוא בA או בB. אם הוא בA אז הוא ב
. לפי ההגדרה של x הוא בA או בB. אם הוא בA אז הוא ב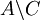 ואם הוא בB אז הוא ב
ואם הוא בB אז הוא ב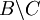 . לכן סה"כ הוא תמיד באגף שמאל לכן אגף ימין מוכל באגף שמאל
. לכן סה"כ הוא תמיד באגף שמאל לכן אגף ימין מוכל באגף שמאל