משתמש:אור שחף/133 - הרצאה/22.3.11
מתוך Math-Wiki
< משתמש:אור שחף | 133 - הרצאה
גרסה מ־14:16, 22 במרץ 2011 מאת אור שחף (שיחה | תרומות) (יצירת דף עם התוכן "===דוגמאות=== # <math>\int\limits_0^2 x^2e^{x^3}}\mathrm dx</math>. שיטה א - נתעלם מהגבולות עד סוף החישוב. נציב <math>t=x^3\...")
דוגמאות
- עיבוד הנוסחה נכשל (שגיאת תחביר): \int\limits_0^2 x^2e^{x^3}}\mathrm dx
. שיטה א - נתעלם מהגבולות עד סוף החישוב. נציב 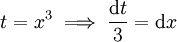 . לכן
. לכן ![\int=\int e^t\frac{\mathrm dt}3=\frac{e^t}3=\left[\frac{e^{x^3}}3\right]_{x=0}^2=\frac{e^8-1}3](/images/math/c/1/7/c1764f07b38b4f5fc2a98dc5e07a519e.png) . דרך ב - נחליף את הגבולות בדרך:
. דרך ב - נחליף את הגבולות בדרך: 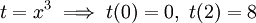 ולכן עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \int=\limits_0^8\frac{e^t}3\mathrm dt=\left[\frac{e^t}3\right]_{t=0}^8=\frac{e^8-1}3
ולכן עיבוד הנוסחה נכשל (ההמרה ל־PNG נכשלה; אנא בדקו אם התקנתם נכון את latex ואת dvipng (או צירוף של dvips, gs ו־convert)): \int=\limits_0^8\frac{e^t}3\mathrm dt=\left[\frac{e^t}3\right]_{t=0}^8=\frac{e^8-1}3
- נחשב שטח עיגול בעל רדיוס r.
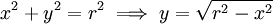 . לכן השטח הוא
. לכן השטח הוא 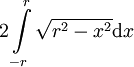 . נציב
. נציב 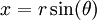 ... הערה: כאשר החלפנו את גבולות האינטגרציה בהצגה
... הערה: כאשר החלפנו את גבולות האינטגרציה בהצגה 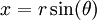 היינו צריכים לבחור
היינו צריכים לבחור 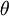 כך ש-
כך ש-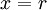 , אבל יכולנו לבחור
, אבל יכולנו לבחור 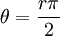 כי אז
כי אז 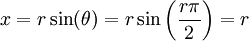 , ועבור
, ועבור 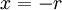 יכולנו לבחור
יכולנו לבחור 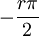 . אם כן היינו מוצאים
. אם כן היינו מוצאים 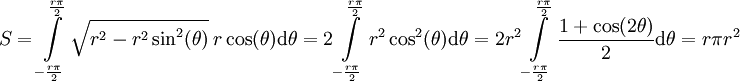 . הטעות נובעת מכך שקבענו ש-
. הטעות נובעת מכך שקבענו ש-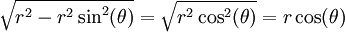 , מה שנכון רק כאשר
, מה שנכון רק כאשר 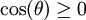 . הטווח של האינטגרציה היה
. הטווח של האינטגרציה היה ![\left[-\frac{r\pi}2,\frac{r\pi}2\right]](/images/math/9/c/e/9ce51cd7682cb87fd3c5249ea9da5741.png) , שכולל תחומים בהם
, שכולל תחומים בהם 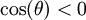 . בתחומים אלה צריך לבחור
. בתחומים אלה צריך לבחור 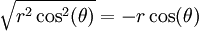 ולחלק את הקטע
ולחלק את הקטע ![\left[-\frac{r\pi}2,\frac{r\pi}2\right]](/images/math/9/c/e/9ce51cd7682cb87fd3c5249ea9da5741.png) לתחומים שונים לפי הסימן של
לתחומים שונים לפי הסימן של 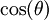 .
.
יישומים של אינטגרציה
- אם בקטע
![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) מתקיים
מתקיים 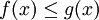 כבר ראינו שהשטח בין הגרפים הוא
כבר ראינו שהשטח בין הגרפים הוא 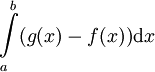 .
. - נפח של גוף סיבוב גרף (1). נסובב את השטח מתחת לגרף
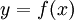 בין a ל-b סביב ציר ה-x ונחשב את הנפח הנוצר. עבור
בין a ל-b סביב ציר ה-x ונחשב את הנפח הנוצר. עבור 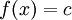 קבוע הסיבוב יוצר גליל שנפחו ידוע לנו -
קבוע הסיבוב יוצר גליל שנפחו ידוע לנו - 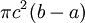 . כעת נניח ש-
. כעת נניח ש-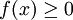 רציפה ב-
רציפה ב-![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ונחשב את הנפח הנוצר ע"י סיבוב הגרף. ובכן: נקח חלוקה כלשהי P של
ונחשב את הנפח הנוצר ע"י סיבוב הגרף. ובכן: נקח חלוקה כלשהי P של ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) ,
, 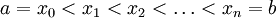 . תחילה נעיין בנפח הנוצר כאשר אותו חלק מהגרף שמעל
. תחילה נעיין בנפח הנוצר כאשר אותו חלק מהגרף שמעל ![[x_{k-1},x_k]](/images/math/2/2/4/224be76d80cdbec9a700c2096afa4264.png) מסתובב סביב ציר ה-x עפ"י המשפט השני של וירשטרס יש ל-f מקסימום
מסתובב סביב ציר ה-x עפ"י המשפט השני של וירשטרס יש ל-f מקסימום 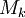 ומינימום
ומינימום 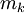 בקטע זה. נסמן ב-
בקטע זה. נסמן ב-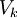 הנפח שנוצר ע"י חלק זה של הגרף. אז מתקיים
הנפח שנוצר ע"י חלק זה של הגרף. אז מתקיים 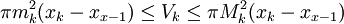 . יוצא שהנפח בסה"כ הוא
. יוצא שהנפח בסה"כ הוא 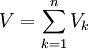 ומתקיים
ומתקיים 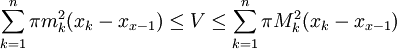 . נעיר שהסכום בצד ימין הוא בדיוק
. נעיר שהסכום בצד ימין הוא בדיוק 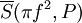 ובצד שמאל
ובצד שמאל 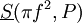 . ז"א לכל חלוקה P
. ז"א לכל חלוקה P 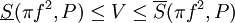 . נשאיף
. נשאיף 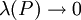 וכיוון ש-f רציפה גם
וכיוון ש-f רציפה גם 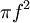 רציפה ולכן שני הסכומים הנ"ל שואפים לאותו הגבול
רציפה ולכן שני הסכומים הנ"ל שואפים לאותו הגבול 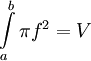 .
.
דוגמאות
- נחשב נפח של כדור בעל רדיוס r:
![V=\pi\int\limits_{-r}^r f^2=\pi\int\limits_{-r}^r (r^2-x^2)\mathrm dx=\pi\left[r^2x-\frac{x^3}3\right]_{x=-r}^r=2\pi(r^3-\frac{r^3}3)=\frac43\pi r^3](/images/math/4/f/a/4fa55419af890bc8c3cb89cf7e77d692.png) .
. - נחשב נפח של חרוט בעל גובה h ורדיוס בסיס r. גרף (3) זהו גרף סיבוב המתקבל מסיבוב משולש סביב ציר ה-x. גרף (4)
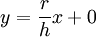 . לפי זה הנפח הוא עיבוד הנוסחה נכשל (שגיאת תחביר): \pi\int\limits_0^h\left(\frac rhx\right)^2\mathrm dx=\pi(\frac rh)^2\int\limits_0^h x^2\mathrm dx=\pi\left(\frac rh\right)^2\frac{x^3}3\right]_{x=0}^h=\frac{\pi r^2h}3
. לפי זה הנפח הוא עיבוד הנוסחה נכשל (שגיאת תחביר): \pi\int\limits_0^h\left(\frac rhx\right)^2\mathrm dx=\pi(\frac rh)^2\int\limits_0^h x^2\mathrm dx=\pi\left(\frac rh\right)^2\frac{x^3}3\right]_{x=0}^h=\frac{\pi r^2h}3
, כלומר נפח החרוט הוא שליש מנפח הגליל בעל אותו גובה ורדיוס בסיסים.
- נגדיר ממוצע של פונקציה רציפה: תהא f מוגדרת ורציפה