סיבוכיות
מתוך Math-Wiki
סיבוכיות היא דרך להשוות בין קצב גידול של פונקציות ממשיות. הסיבוכיות של פונקציה אינה מושפעת מהכפלתה בקבוע (גדול מ-0).
או גדול, אומגה, תטה
הגדרה תהיינה 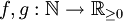 פונקציות אי שליליות מהטבעיים לממשיים.
פונקציות אי שליליות מהטבעיים לממשיים.
- נאמר ש-
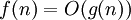 אם קיים
אם קיים 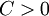 ממשי ו-
ממשי ו-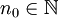 כך ש-
כך ש-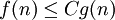 לכל
לכל 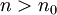 (הקבוע
(הקבוע 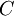 יכול להיות גדול כרצוננו).
יכול להיות גדול כרצוננו). - נאמר ש-
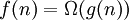 אם קיים
אם קיים 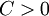 ממשי ו-
ממשי ו-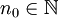 כך ש-
כך ש-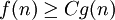 לכל
לכל 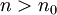 (הקבוע
(הקבוע 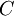 יכול קטן גדול כרצוננו).
יכול קטן גדול כרצוננו). - נאמר ש-
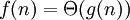 אם
אם 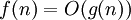 וגם
וגם 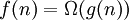 , כלומר קיימים
, כלומר קיימים 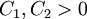 ממשיים ו-
ממשיים ו-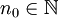 כך ש-
כך ש-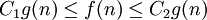 לכל
לכל 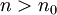 .
.
לעיתים משתמשים גם בהגדה הבאה:
- נאמר ש-
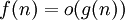 (סימון אחר
(סימון אחר 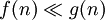 ) אם
) אם 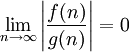 . (הגדרה זו תקפה גם עבור פונקציות המקבלות ערכים שליליים ולכן הערך המוחלט.)
. (הגדרה זו תקפה גם עבור פונקציות המקבלות ערכים שליליים ולכן הערך המוחלט.)
דוגמא: אם 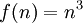 ו-
ו-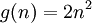 אז לא קשה לראות ש-
אז לא קשה לראות ש-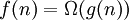 ו-
ו-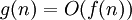 אבל לא מתקיים
אבל לא מתקיים 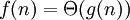 .
.
קצת אינטואיציה: 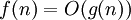 אומר ש-
אומר ש- גדלה כמו
גדלה כמו 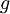 או פחות מכך (עד כדי כפל בקבוע).
או פחות מכך (עד כדי כפל בקבוע). 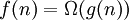 אומר ש-
אומר ש- גדלה כמו
גדלה כמו 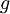 או יותר מכך (עד כדי כפל בקבוע).
או יותר מכך (עד כדי כפל בקבוע).
הערה: כשכותבים 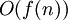 בחישובים (לדוגמא:
בחישובים (לדוגמא: 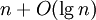 ) בדרך כלל מתכוונים לפונקציה שהיא
) בדרך כלל מתכוונים לפונקציה שהיא 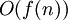 . הנ"ל נכון גם עבור
. הנ"ל נכון גם עבור 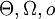 .
.
הערה: ההגדרות לעיל תקפות גם עבור פונקציות מ-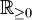 ל-
ל-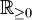
תכונות בסיסיות
נניח כי 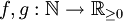 אזי:
אזי:
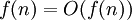 . כנ"ל עבור
. כנ"ל עבור 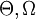 . (זהירות:
. (זהירות: 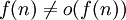 !)
!)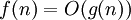 אם ורק אם
אם ורק אם 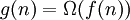 .
.-
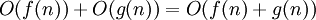 . כנ"ל עבור
. כנ"ל עבור 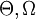 .
. -
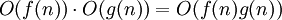 . כנ"ל עבור
. כנ"ל עבור 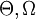 .
. -
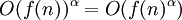 לכל
לכל 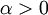 . כנ"ל עבור
. כנ"ל עבור 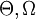 .
. - היחס
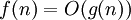 הוא טרנזיטיבי. (ניסוח אחר:
הוא טרנזיטיבי. (ניסוח אחר: 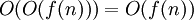 .) כנ"ל עבור
.) כנ"ל עבור 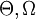 .
. - היחס
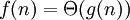 הוא יחס שקילות.
הוא יחס שקילות. -
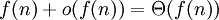 .
.
יחסים בין פונקציות נפוצות
- לכל
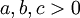 ו-
ו-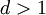 ממשיים מתקיים
ממשיים מתקיים 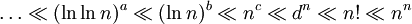 .
. - לכל
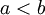 ממשיים
ממשיים 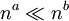 .
. - לכל
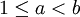 ממשיים
ממשיים 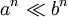 .
.