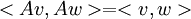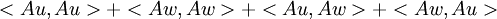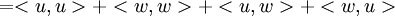הבדלים בין גרסאות בדף "עמוד ראשי"
(←תיקון לתרגיל 7) |
(←תיקון לתרגיל 7) |
||
| שורה 106: | שורה 106: | ||
*שימו לב לגרסא הפוסט-אחרונה לתרגיל 7. וקטור האפס בשאלה 3.a הוא עם 2 קואורדינטות ולא 3 | *שימו לב לגרסא הפוסט-אחרונה לתרגיל 7. וקטור האפס בשאלה 3.a הוא עם 2 קואורדינטות ולא 3 | ||
*שימו לב לגרסא הפוסט-אחרונה-חביבה לתרגיל 7. בשאלה 2 אתם נדרשים לחשב נפח של פוליטופ ולא סתם פוליטופ... | *שימו לב לגרסא הפוסט-אחרונה-חביבה לתרגיל 7. בשאלה 2 אתם נדרשים לחשב נפח של פוליטופ ולא סתם פוליטופ... | ||
| + | |||
| + | ===השלמה לתרגיל, לתלמידי כל המתרגלים=== | ||
| + | בתרגיל הראנו שכל מטריצה <math>A</math> ששומרת נורמה שומרת מכפלה פנימית מעל הממשים. כלומר אם <math>\forall v \in V:||Av||=||v||</math> אזי גם <math>\forall v,w \in V: <Av,Aw>=<v,w></math>. | ||
| + | |||
| + | |||
| + | '''הוכחה''': | ||
| + | |||
| + | <math>A</math> שומרת נורמה ולכן <math>\forall v \in V:||Av||=||v||</math>, ניקח <math>v=w+u</math> אזי <math>||A(u+w)||=||u+w||</math> ולכן <math>||A(u+w)||^2=||u+w||^2</math> ולכן <math><A(u+w),A(u+w)>=<u+w,u+w></math>, ולכן <math><Au+Aw,Au+Aw>=<u+w,u+w></math>. נפתח את שני הצדדים לקבל: | ||
| + | |||
| + | |||
| + | :<math><Au,Au>+<Aw,Aw>+<Au,Aw>+<Aw,Au></math> | ||
| + | |||
| + | :<math>=<u,u>+<w,w>+<u,w>+<w,u></math> | ||
| + | |||
| + | |||
| + | אבל מעל הממשיים המכפלה הפנימית היא סימטרית ולכן: | ||
| + | |||
| + | <math><Au,Au>+<Aw,Aw>+2<Au,Aw>=<u,u>+<w,w>+2<u,w></math> | ||
| + | |||
| + | <math>||Au||^2+||Aw||^2+2<Au,Aw>=||u||^2+||w||^2+2<u,w></math> | ||
| + | |||
| + | <math>A</math> שומרת על נורמה ולכן אפשר לצמצם ולקבל | ||
| + | |||
| + | <math>2<Au,Aw>=2<u,w></math> | ||
| + | |||
| + | נחלק ב2 לקבל את שרצינו. | ||
| + | |||
| + | |||
| + | '''הוכחה מעל המרוכבים''': | ||
| + | |||
| + | כעת, אם אנחנו מעל המרוכבים, המכפלה הפנימית אינה סימטרית אלא הרמיטית. ולכן השיוויון יהיה: | ||
| + | |||
| + | <math><Au,Aw>+\overline{<Au,Aw>}=<u,w>+\overline{<u,w>}</math> | ||
| + | |||
| + | ולכן <math>2Re(<Au,Aw>)=2Re(<u,w>)</math>. | ||
| + | |||
| + | נותר להוכיח שיוויון גם עבור החלק המדומה. ניקח <math>v=u+iw</math> ונקבל: | ||
| + | |||
| + | <math><Au+iAw,Au+iAw>=<Au,Au>+<iAw,iAw>+<Au,iAw>+<iAw,Au></math> | ||
| + | |||
| + | <math>=<Au,Au>+i\overline{i}<Aw,Aw>+\overline{i}<Au,Aw>+i<Aw,Au></math> | ||
| + | |||
| + | <math>=<Au,Au>+<Aw,Aw>-i\cdot\overline{<Au,Aw>}+i<Au,Aw></math> | ||
| + | |||
| + | <math>=<Au,Au>+<Aw,Aw>+\overline{i<Au,Aw>}+i<Au,Aw></math> | ||
| + | |||
| + | <math>=||Au||^2+||Aw||^2+2Re(i<Au,Aw>)</math> | ||
| + | |||
| + | <math>=||Au||^2+||Aw||^2-2Im(<Au,Aw>)</math> | ||
| + | |||
| + | וע"י פיתוח הצד השני נקבל את השיוויון עבור החלק המדומה, וסה"כ נקבל <math><Av,Aw>=<v,w></math> | ||
גרסה מ־21:46, 12 בדצמבר 2009
תוכן עניינים
- 1 משוב והערות למרצים ולמתרגלים
- 2 חוברת הקורס אלגברה לינארית של ד"ר בועז צבאן
- 3 אינפי 1 לתיכוניסטים
- 4 לינארית 2 לתיכוניסטים
- 4.1 השלמה להרצאה
- 4.2 הוכחת משפט לפלס
- 4.3 דוגמא לליכסון מטריצה
- 4.4 אלגוריתם לשילוש מטריצה
- 4.5 השלמה לקבוצה של ד"ר צבאן
- 4.6 בוחן בקורס: ביום ג' שאחרי חנוכה
- 4.7 תיקון/השלמה לתרגיל - לתלמידי כל המתרגלים
- 4.8 תיקון/השלמה שנייה לתרגיל - לתלמידי כל המתרגלים
- 4.9 שאלת הבונוס
- 4.10 תיקון לתרגיל 7
- 4.11 השלמה לתרגיל, לתלמידי כל המתרגלים
משוב והערות למרצים ולמתרגלים
חוברת הקורס אלגברה לינארית של ד"ר בועז צבאן
אינפי 1 לתיכוניסטים
לינארית 2 לתיכוניסטים
השלמה להרצאה
דוגמא יפה שמראה שלכל פולינום מתוקן, יש מטריצה שהוא הפולינום האפייני שלה.
(לקריאה עצמית על ידי התלמיד)
הוכחת משפט לפלס
(לקריאה עצמית על ידי התלמיד)
דוגמא לליכסון מטריצה
הערה: שימו לב שעמודות המטריצה M הינן וקטורים עצמיים של המטריצה המהווים בסיס.
אלגוריתם לשילוש מטריצה
ניתן לקרוא בחוברת בעמוד 88: משפט השילוש ושאלה 4.2. בנוסף אפשר לקרוא בדף השאלות ותשובות
השלמה לקבוצה של ד"ר צבאן
החלק החסר מההוכחה בסוף השיעור.
(לקריאה עצמית על ידי התלמיד)
בוחן בקורס: ביום ג' שאחרי חנוכה
ביום ג', 22 דצמבר, בשעה שלש וחצי (במקום ההרצאה) ייערך בוחן על כל החומר שיילמד עד חנוכה.
איפה הבוחן? בניין 501, חדר 160 (אולם הספורט לשעבר, הכניסה ליד מגרש הספורט).
מה ללמוד לבוחן? מה שלמדנו בהרצאה ובתרגיל, עד חנוכה. (בחנוכה אין לימודים בקורס שלנו.) זה כולל הגדרות, ניסוח מדוייק והוכחות משפטים, משפטונים (שמשפטונים אפשר להוכיח גם כשלא זוכרים את ההוכחה מהכתה), ויכולת פתרון תרגילים ברמת קושי דומה לתרגילי הבית.
מטרות הבוחן:
1. הבאת ההתלמיד להבנה טובה של החומר שנלמד עד שלב זה, שתאפשר לו להתמודד עם המשך הקורס בצורה טובה.
2. נקודת ביקורת, שבה התלמיד מעריך את הידע והטכניקה הנוכחיים, במטרה לראות האם עליו לשפרם בצורה משמעותית לקראת המבחן.
מתי כדאי ללמוד לבוחן? מי שפנוי לכך בימי החנוכה, זה הזמן המומלץ ביותר. מי שלא, יכול ללמוד עד חנוכה, ולרענן את זכרונו מיום ראשון עד יום שלישי.
ואם יהיו לנו שאלות? ד"ר צבאן יעביר בהתנדבות שיעור ביום חמישי שחל בחנוכה (17 דצמבר), בשעות שתיים עד ארבע, בניין 105, חדר 106. השיעור הוא רשות, מיועד רק למי שיש לו שאלות או רוצה לשמוע תשובות לשאלות של האחרים, ופתוח לתלמידי שתי הקבוצות.
מה משקל הבוחן בציון הסופי? הבוחן הוא עשר אחוזים מהציון הסופי. למשל, מי שיקבל חמישים בבוחן, ציונו הסופי יהיה לכל היותר (בהנחה ששיפר את יכולותיו עד המבחן) תשעים וחמש.
ואם איני יכול להגיע לבוחן מסיבה מוצדקת? כעיקרון, אין הרבה סיבות מוצדקות להיעדר מהבוחן. במקרים מאד חריגים (שאנו מקוים שלא יהיו), ומגובים על ידי מסמכים רשמיים, ננסה לטפל בצורה פרטנית. לא מובטח שהפתרון למקרים כאלה יהיה אופטימלי, אך נעשה כמיטב יכלתנו לפתור את הבעיה לפחות חלקית.
תיקון/השלמה לתרגיל - לתלמידי כל המתרגלים
יהיה  ממ"פ ממימד
ממ"פ ממימד  . יהיו וקטורים
. יהיו וקטורים 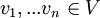 . נגדיר את מטריצת גרהם
. נגדיר את מטריצת גרהם  ע"י
ע"י 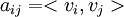 . הוכח:
. הוכח:
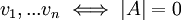 ת"ל
ת"ל
תיקון/השלמה שנייה לתרגיל - לתלמידי כל המתרגלים
 לכסינה
לכסינה 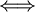 הפולינום המינימלי שלה הוא מהצורה
הפולינום המינימלי שלה הוא מהצורה 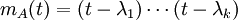 עבור
עבור 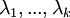 הע"ע השונים של
הע"ע השונים של 
שאלת הבונוס
תהי 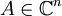 הפיכה, ונתון ש
הפיכה, ונתון ש 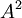 לכסינה. הוכח ש
לכסינה. הוכח ש לכסינה.
לכסינה.
הפתרונות עברו לדף הבא: דף הבונוס
הפותרים: רום דודקביץ, עידו קוטלר, דניאל ורדי-זר, אסף רוזן, ניל וקסלר, עדן קופרווסר
תיקון לתרגיל 7
- שימו לב לגרסא האחרונה לתרגיל 7. יש ערך מוחלט סביב
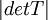 בשאלה 1.b
בשאלה 1.b - שימו לב לגרסא הפוסט-אחרונה לתרגיל 7. וקטור האפס בשאלה 3.a הוא עם 2 קואורדינטות ולא 3
- שימו לב לגרסא הפוסט-אחרונה-חביבה לתרגיל 7. בשאלה 2 אתם נדרשים לחשב נפח של פוליטופ ולא סתם פוליטופ...
השלמה לתרגיל, לתלמידי כל המתרגלים
בתרגיל הראנו שכל מטריצה  ששומרת נורמה שומרת מכפלה פנימית מעל הממשים. כלומר אם
ששומרת נורמה שומרת מכפלה פנימית מעל הממשים. כלומר אם 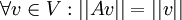 אזי גם
אזי גם 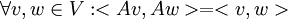 .
.
הוכחה:
 שומרת נורמה ולכן
שומרת נורמה ולכן 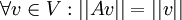 , ניקח
, ניקח 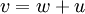 אזי
אזי 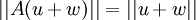 ולכן
ולכן 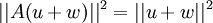 ולכן
ולכן 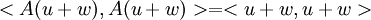 , ולכן
, ולכן 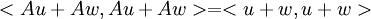 . נפתח את שני הצדדים לקבל:
. נפתח את שני הצדדים לקבל:
אבל מעל הממשיים המכפלה הפנימית היא סימטרית ולכן:
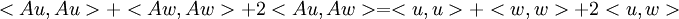
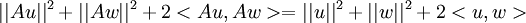
 שומרת על נורמה ולכן אפשר לצמצם ולקבל
שומרת על נורמה ולכן אפשר לצמצם ולקבל
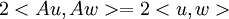
נחלק ב2 לקבל את שרצינו.
הוכחה מעל המרוכבים:
כעת, אם אנחנו מעל המרוכבים, המכפלה הפנימית אינה סימטרית אלא הרמיטית. ולכן השיוויון יהיה:
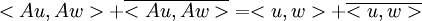
ולכן 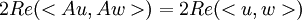 .
.
נותר להוכיח שיוויון גם עבור החלק המדומה. ניקח 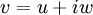 ונקבל:
ונקבל:
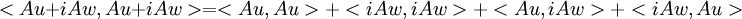
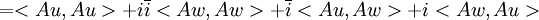
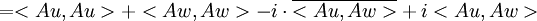
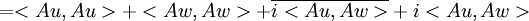
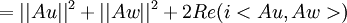
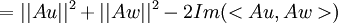
וע"י פיתוח הצד השני נקבל את השיוויון עבור החלק המדומה, וסה"כ נקבל