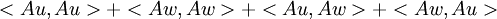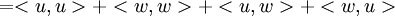עמוד ראשי
תוכן עניינים
- 1 משוב והערות למרצים ולמתרגלים
- 2 חוברת הקורס אלגברה לינארית של ד"ר בועז צבאן
- 3 אינפי 1 לתיכוניסטים
- 4 לינארית 2 לתיכוניסטים
- 4.1 מבחן
- 4.2 שילוש אורתוגונאלי
- 4.3 שניוניות
- 4.4 לכסון אורתוגונלי
- 4.5 שימו לב: תיקון תרגיל 12
- 4.6 הודעה לתלמידי שתי הקבוצות
- 4.7 השלמה לכתה של ד"ר צבאן בנושא מיון שניוניות (מיון המקרה הנותר ומקרים פרטיים חשובים)
- 4.8 ציונים בבוחן!
- 4.9 שימו לב: תרגיל 10
- 4.10 שימו לב: תרגיל 10
- 4.11 שימו לב: תרגיל 8
- 4.12 השלמה לתרגיל, לתלמידי כל המתרגלים
- 4.13 תיקון לתרגיל 7
- 4.14 שאלת הבונוס
- 4.15 תיקון/השלמה שנייה לתרגיל - לתלמידי כל המתרגלים
- 4.16 תיקון/השלמה לתרגיל - לתלמידי כל המתרגלים
- 4.17 בוחן בקורס: ביום ג' שאחרי חנוכה
- 4.18 השלמה לקבוצה של ד"ר צבאן
- 4.19 אלגוריתם לשילוש מטריצה
- 4.20 דוגמא לליכסון מטריצה
- 4.21 הוכחת משפט לפלס
- 4.22 השלמה להרצאה
משוב והערות למרצים ולמתרגלים
חוברת הקורס אלגברה לינארית של ד"ר בועז צבאן
אינפי 1 לתיכוניסטים
לינארית 2 לתיכוניסטים
מבחן
מספר הערות בנוגע למבחן:
- ככל שרמת ההבנה של הוכחות המשפטים גדלה, כך קל יותר לדעת להוכיח אותם במבחן (זוכרים את ה"טריקים" העיקריים ואז משלימים את החסר). לכן מומלץ כתהליך הלמידה למבחן להבין את החומר ולא לשנן את כולו.
- לגבי שניוניות: אין צורך לזכור את כל שמות השניוניות בעל פה. יש לדעת לפשט שניונית לצורתה הפשוטה ביותר, כלומר צורה בה כל משתנה מופיע לכל היותר פעם אחת (או בריבוע, או בחזקת אחד או שבכלל אינו מופיע), ובמידת האפשר יש לאפס את הקבוע (אם אחד המשתנים מופיע בצורתו הלינארית, הוא יכול "לבלוע" את הקבוע על ידי הזזה).
- חומר הקורס מסודר לנושאים, מומלץ ללמוד נושא מההרצאה, ואז מהתרגיל ואז לפתור תרגילים בנושא מתרגילי הבית או תרגילים ממבחנים ולאחר מכן לבדוק את עצמכם מול הפתרונות. לאחר שאתם מרגישים שאתם שולטים בנושא מסוים, תעברו לנושא הבא.
- האתר נשאר פעיל עד לזמן בלתי מוגבל, תנצלו אותו. גם אם אין לכם שאלות, כדאי לקרוא שאלות של אחרים, הם יכולים לרענן את החשיבה שלכם.
- לגבי משפט אוילר, הוא מחולק לחלק מתמטי וחלק פיסיקלי. את החלק הפיסיקלי לא צריך לדעת למבחן, אבל את החלק המתמטי כן (וכל המשפטונים שמובילים להוכחה כמובן).
שילוש אורתוגונאלי
דוגמא לשילוש אורתוגונאלי כאשר השילוש אינו טריוויאלי.
שניוניות
יש כבר פתרון לתרגיל 12 בנושא שניוניות, הפתרון חוזר על האלגוריתם שראינו בכיתה. למי שעוד מתקשה בנושא לכסון א"ג ראו הערה אחת למטה.
לכסון אורתוגונלי
למי שלא הבין כיצד לבצע לכסון אורתוגונלי, צירפנו את הדף הבא
שימו לב: תיקון תרגיל 12
שימו לב לתיקון שנוסף לתרגיל 12, שאלה 3.
הודעה לתלמידי שתי הקבוצות
חפשו בויקיפדיה את המונח Quadric, שם תמצאו דוגמאות איך נראות השניוניות במרחב  עבור כל אחד מהמקרים החשובים
עבור כל אחד מהמקרים החשובים
השלמה לכתה של ד"ר צבאן בנושא מיון שניוניות (מיון המקרה הנותר ומקרים פרטיים חשובים)
ציונים בבוחן!
שימו לב שבעקבות כתב החרטומים של חלק מיכם ייתכנו טעויות בת.ז. שלכם, לכן תבחרו בזו שהכי קרובה לאמיתית.
שימו לב: תרגיל 10
תיקון: בשאלה 3, המטריצה הנתונה הינה הפיכה.
הארכה: אפשר להגיש את התרגיל בשבוע הבא, בנוסף לתרגיל 11 שיפורסם מחר.
שימו לב: תרגיל 10
שימו לב לתוספת שאלה 6 בתרגיל 10.
שימו לב: תרגיל 8
הוספנו את תרגיל 8, תרגיל יחסית קליל על מנת להשאיר זמן ללמוד לבוחן.
השלמה לתרגיל, לתלמידי כל המתרגלים
בתרגיל הראנו שכל מטריצה  ששומרת נורמה שומרת מכפלה פנימית מעל הממשים. כלומר אם
ששומרת נורמה שומרת מכפלה פנימית מעל הממשים. כלומר אם 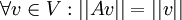 אזי גם
אזי גם 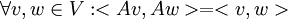 .
.
הוכחה:
 שומרת נורמה ולכן
שומרת נורמה ולכן 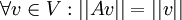 , ניקח
, ניקח 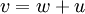 אזי
אזי 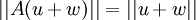 ולכן
ולכן 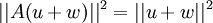 ולכן
ולכן 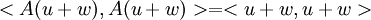 , ולכן
, ולכן 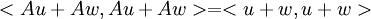 . נפתח את שני הצדדים לקבל:
. נפתח את שני הצדדים לקבל:
אבל מעל הממשיים המכפלה הפנימית היא סימטרית ולכן:
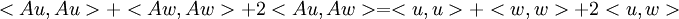
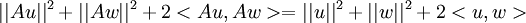
 שומרת על נורמה ולכן אפשר לצמצם ולקבל
שומרת על נורמה ולכן אפשר לצמצם ולקבל
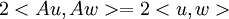
נחלק ב2 לקבל את שרצינו.
הוכחה מעל המרוכבים:
כעת, אם אנחנו מעל המרוכבים, המכפלה הפנימית אינה סימטרית אלא הרמיטית. ולכן השיוויון יהיה:
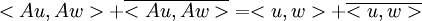
ולכן 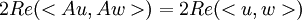 .
.
נותר להוכיח שיוויון גם עבור החלק המדומה. ניקח 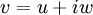 ונקבל:
ונקבל:
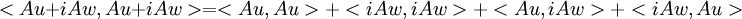
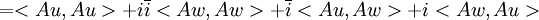
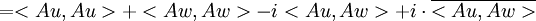
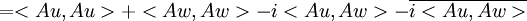
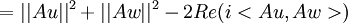
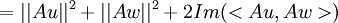
וע"י פיתוח הצד השני נקבל את השיוויון עבור החלק המדומה, וסה"כ נקבל 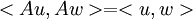
תיקון לתרגיל 7
- שימו לב לגרסא האחרונה לתרגיל 7. יש ערך מוחלט סביב
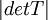 בשאלה 1.b
בשאלה 1.b - שימו לב לגרסא הפוסט-אחרונה לתרגיל 7. וקטור האפס בשאלה 3.a הוא עם 2 קואורדינטות ולא 3
- שימו לב לגרסא הפוסט-אחרונה-חביבה לתרגיל 7. בשאלה 2 אתם נדרשים לחשב נפח של פוליטופ ולא סתם פוליטופ...
שאלת הבונוס
תהי 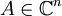 הפיכה, ונתון ש
הפיכה, ונתון ש 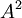 לכסינה. הוכח ש
לכסינה. הוכח ש לכסינה.
לכסינה.
הפתרונות עברו לדף הבא: דף הבונוס
הפותרים: רום דודקביץ, עידו קוטלר, דניאל ורדי-זר, אסף רוזן, ניל וקסלר, עדן קופרווסר
תיקון/השלמה שנייה לתרגיל - לתלמידי כל המתרגלים
 לכסינה
לכסינה 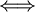 הפולינום המינימלי שלה הוא מהצורה
הפולינום המינימלי שלה הוא מהצורה 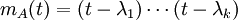 עבור
עבור 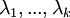 הע"ע השונים של
הע"ע השונים של 
תיקון/השלמה לתרגיל - לתלמידי כל המתרגלים
יהיה  ממ"פ ממימד
ממ"פ ממימד  . יהיו וקטורים
. יהיו וקטורים 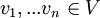 . נגדיר את מטריצת גרהם
. נגדיר את מטריצת גרהם  ע"י
ע"י 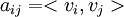 . הוכח:
. הוכח:
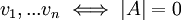 ת"ל
ת"ל
בוחן בקורס: ביום ג' שאחרי חנוכה
ביום ג', 22 דצמבר, בשעה שלש וחצי (במקום ההרצאה) ייערך בוחן על כל החומר שיילמד עד חנוכה.
איפה הבוחן? בניין 501, חדר 160 (אולם הספורט לשעבר, הכניסה ליד מגרש הספורט).
מה ללמוד לבוחן? מה שלמדנו בהרצאה ובתרגיל, עד חנוכה. (בחנוכה אין לימודים בקורס שלנו.) זה כולל הגדרות, ניסוח מדוייק והוכחות משפטים, משפטונים (שמשפטונים אפשר להוכיח גם כשלא זוכרים את ההוכחה מהכתה), ויכולת פתרון תרגילים ברמת קושי דומה לתרגילי הבית.
מטרות הבוחן:
1. הבאת ההתלמיד להבנה טובה של החומר שנלמד עד שלב זה, שתאפשר לו להתמודד עם המשך הקורס בצורה טובה.
2. נקודת ביקורת, שבה התלמיד מעריך את הידע והטכניקה הנוכחיים, במטרה לראות האם עליו לשפרם בצורה משמעותית לקראת המבחן.
מתי כדאי ללמוד לבוחן? מי שפנוי לכך בימי החנוכה, זה הזמן המומלץ ביותר. מי שלא, יכול ללמוד עד חנוכה, ולרענן את זכרונו מיום ראשון עד יום שלישי.
ואם יהיו לנו שאלות? ד"ר צבאן יעביר בהתנדבות שיעור ביום חמישי שחל בחנוכה (17 דצמבר), בשעות שתיים עד ארבע, בניין 105, חדר 106. השיעור הוא רשות, מיועד רק למי שיש לו שאלות או רוצה לשמוע תשובות לשאלות של האחרים, ופתוח לתלמידי שתי הקבוצות.
מה משקל הבוחן בציון הסופי? הבוחן הוא עשר אחוזים מהציון הסופי. למשל, מי שיקבל חמישים בבוחן, ציונו הסופי יהיה לכל היותר (בהנחה ששיפר את יכולותיו עד המבחן) תשעים וחמש.
ואם איני יכול להגיע לבוחן מסיבה מוצדקת? כעיקרון, אין הרבה סיבות מוצדקות להיעדר מהבוחן. במקרים מאד חריגים (שאנו מקוים שלא יהיו), ומגובים על ידי מסמכים רשמיים, ננסה לטפל בצורה פרטנית. לא מובטח שהפתרון למקרים כאלה יהיה אופטימלי, אך נעשה כמיטב יכלתנו לפתור את הבעיה לפחות חלקית.
השלמה לקבוצה של ד"ר צבאן
החלק החסר מההוכחה בסוף השיעור.
(לקריאה עצמית על ידי התלמיד)
אלגוריתם לשילוש מטריצה
ניתן לקרוא בחוברת בעמוד 88: משפט השילוש ושאלה 4.2. בנוסף אפשר לקרוא בדף השאלות ותשובות
דוגמא לליכסון מטריצה
הערה: שימו לב שעמודות המטריצה M הינן וקטורים עצמיים של המטריצה המהווים בסיס.
הוכחת משפט לפלס
(לקריאה עצמית על ידי התלמיד)
השלמה להרצאה
דוגמא יפה שמראה שלכל פולינום מתוקן, יש מטריצה שהוא הפולינום האפייני שלה.
(לקריאה עצמית על ידי התלמיד)