עמוד ראשי
תוכן עניינים
משוב והערות למרצים ולמתרגלים
חוברת הקורס אלגברה לינארית של ד"ר בועז צבאן
אינפי 1 לתיכוניסטים
לינארית 2 לתיכוניסטים
השלמה להרצאה
דוגמא יפה שמראה שלכל פולינום מתוקן, יש מטריצה שהוא הפולינום האפייני שלה.
(לקריאה עצמית על ידי התלמיד)
הוכחת משפט לפלס
(לקריאה עצמית על ידי התלמיד)
דוגמא לליכסון מטריצה
הערה: שימו לב שעמודות המטריצה M הינן וקטורים עצמיים של המטריצה המהווים בסיס.
אלגוריתם לשילוש מטריצה
ניתן לקרוא בחוברת בעמוד 88: משפט השילוש ושאלה 4.2. בנוסף אפשר לקרוא בדף השאלות ותשובות
השלמה לקבוצה של ד"ר צבאן
החלק החסר מההוכחה בסוף השיעור.
(לקריאה עצמית על ידי התלמיד)
בוחן בקורס: ביום ג' שאחרי חנוכה
ביום ג', 22 דצמבר, בשעה שלש וחצי (במקום ההרצאה) ייערך בוחן על כל החומר שיילמד עד חנוכה.
איפה הבוחן? בניין 501, חדר 160 (אולם הספורט לשעבר, הכניסה ליד מגרש הספורט).
מה ללמוד לבוחן? מה שלמדנו בהרצאה ובתרגיל, עד חנוכה. (בחנוכה אין לימודים בקורס שלנו.) זה כולל הגדרות, ניסוח מדוייק והוכחות משפטים, משפטונים (שמשפטונים אפשר להוכיח גם כשלא זוכרים את ההוכחה מהכתה), ויכולת פתרון תרגילים ברמת קושי דומה לתרגילי הבית.
מטרות הבוחן:
1. הבאת ההתלמיד להבנה טובה של החומר שנלמד עד שלב זה, שתאפשר לו להתמודד עם המשך הקורס בצורה טובה.
2. נקודת ביקורת, שבה התלמיד מעריך את הידע והטכניקה הנוכחיים, במטרה לראות האם עליו לשפרם בצורה משמעותית לקראת המבחן.
מתי כדאי ללמוד לבוחן? מי שפנוי לכך בימי החנוכה, זה הזמן המומלץ ביותר. מי שלא, יכול ללמוד עד חנוכה, ולרענן את זכרונו מיום ראשון עד יום שלישי.
ואם יהיו לנו שאלות? ד"ר צבאן יעביר בהתנדבות שיעור ביום חמישי שחל בחנוכה (17 דצמבר), בשעות שתיים עד ארבע, בניין 105, חדר 106. השיעור הוא רשות, מיועד רק למי שיש לו שאלות או רוצה לשמוע תשובות לשאלות של האחרים, ופתוח לתלמידי שתי הקבוצות.
מה משקל הבוחן בציון הסופי? הבוחן הוא עשר אחוזים מהציון הסופי. למשל, מי שיקבל חמישים בבוחן, ציונו הסופי יהיה לכל היותר (בהנחה ששיפר את יכולותיו עד המבחן) תשעים וחמש.
ואם איני יכול להגיע לבוחן מסיבה מוצדקת? כעיקרון, אין הרבה סיבות מוצדקות להיעדר מהבוחן. במקרים מאד חריגים (שאנו מקוים שלא יהיו), ומגובים על ידי מסמכים רשמיים, ננסה לטפל בצורה פרטנית. לא מובטח שהפתרון למקרים כאלה יהיה אופטימלי, אך נעשה כמיטב יכלתנו לפתור את הבעיה לפחות חלקית.
תיקון/השלמה לתרגיל - לתלמידי כל המתרגלים
יהיה  ממ"פ ממימד
ממ"פ ממימד  . יהיו וקטורים
. יהיו וקטורים 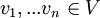 . נגדיר את מטריצת גרהם
. נגדיר את מטריצת גרהם  ע"י
ע"י 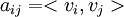 . הוכח:
. הוכח:
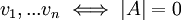 ת"ל
ת"ל
תיקון/השלמה שנייה לתרגיל - לתלמידי כל המתרגלים
 לכסינה
לכסינה 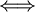 הפולינום המינימלי שלה הוא מהצורה
הפולינום המינימלי שלה הוא מהצורה 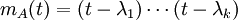 עבור
עבור 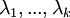 הע"ע השונים של
הע"ע השונים של 
שאלת הבונוס
תהי 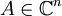 הפיכה, ונתון ש
הפיכה, ונתון ש 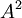 לכסינה. הוכח ש
לכסינה. הוכח ש לכסינה.
לכסינה.
יש פותרים לשאלת הבונוס. השאלה נפתרה בשלוש דרכים עיקריות:
1. הפותרים: רום דודקביץ ועידו קוטלר
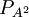 מתפרק לגורמים לינאריים כי אנחנו מעל המרוכבים. לכן
מתפרק לגורמים לינאריים כי אנחנו מעל המרוכבים. לכן 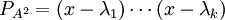 . המטריצה
. המטריצה  הפיכה ולכן גם
הפיכה ולכן גם 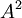 הפיכה, ולכן אין לה ע"ע אפס (לפי משפט). לכן לכל
הפיכה, ולכן אין לה ע"ע אפס (לפי משפט). לכן לכל 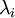 קיימים שני שורשים שונים
קיימים שני שורשים שונים 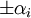 כך ש
כך ש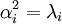 .
.
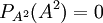 כלומר לכן
כלומר לכן
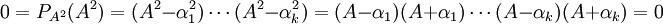 .
.
נסמן 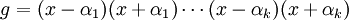 וקבלנו ש
וקבלנו ש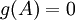 ולכן הפולינום המינימלי של
ולכן הפולינום המינימלי של  מחלק את
מחלק את 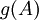 . אבל
. אבל 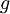 מכיל גורמים לינאריים בלבד ולכן גם הפולינום המינימלי של
מכיל גורמים לינאריים בלבד ולכן גם הפולינום המינימלי של  מכיל גורמים לינאריים בלבד (שימו לב, אם אפס היה ע"ע אז היה גורם
מכיל גורמים לינאריים בלבד (שימו לב, אם אפס היה ע"ע אז היה גורם 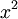 לא לינארי). ולכן ולפי משפט (ראה תיקון/השלמה שנייה)
לא לינארי). ולכן ולפי משפט (ראה תיקון/השלמה שנייה)  לכסינה.
לכסינה.
2. הפותרים: דניאל ורדי-זר, אסף רוזן וניל וקסלר
אנחנו מעל המרוכבים אז לכל מטריצה יש צורת ז'ורדן. תהיי 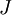 צורת הז'ורדן של
צורת הז'ורדן של  . אזי
. אזי 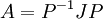 , נעלה בריבוע ונקבל
, נעלה בריבוע ונקבל 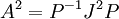 כלומר
כלומר 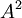 ו
ו 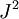 דומות.
דומות.
נניח בשלילה ש לא לכסינה ונוכיח שנובע ש
לא לכסינה ונוכיח שנובע ש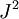 לא לכסינה וזו סתירה לכך ש
לא לכסינה וזו סתירה לכך ש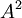 לכסינה.
לכסינה.
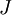 היא סכום ישר של בלוקים, ולכן
היא סכום ישר של בלוקים, ולכן 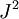 היא סכום ישר של הבלוקים של
היא סכום ישר של הבלוקים של 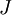 בריבוע. הנחנו ש
בריבוע. הנחנו ש לא לכסינה, לכן בצורת הז'ורדן שלה
לא לכסינה, לכן בצורת הז'ורדן שלה 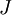 יש בלוק בגודל גדול או שווה ל2 (אחרת כל הבלוקים בגודל אחד וזו מטריצה אלכסונית).
יש בלוק בגודל גדול או שווה ל2 (אחרת כל הבלוקים בגודל אחד וזו מטריצה אלכסונית).
נניח 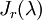 בלוק ז'ורדן ב
בלוק ז'ורדן ב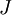 כך ש
כך ש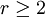 . מכיוון ש
. מכיוון ש הפיכה אין לה ע"ע אפס! ולכן
הפיכה אין לה ע"ע אפס! ולכן 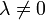 . לכן בהכרח (תרגיל)
. לכן בהכרח (תרגיל) 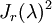 מכיל איברים שאינם אפסים מעל האלכסון, והאלכסון שלו מכיל את
מכיל איברים שאינם אפסים מעל האלכסון, והאלכסון שלו מכיל את 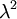 . ולכן
. ולכן 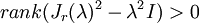 . לכן יש ל
. לכן יש ל 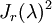 פחות מ
פחות מ 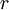 וקטורים עצמיים בת"ל.
וקטורים עצמיים בת"ל.
לפי משפט, כמות הוקטורים העצמיים הבת"ל של מטריצה שהיא סכום ישר של מטריצות, היא סכום כמויות הוקטורים העצמיים הבת"ל בכל אחת מן המטריצות. זה נכון כי 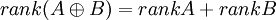 . אבל הראנו שיש בסכום הישר של המטריצה
. אבל הראנו שיש בסכום הישר של המטריצה 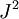 את הבלוק
את הבלוק 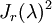 שתורם פחות מ
שתורם פחות מ 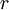 וקטורים עצמיים בת"ל. ולכן לכל המטריצה
וקטורים עצמיים בת"ל. ולכן לכל המטריצה 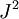 יש פחות מ
יש פחות מ וקטורים עצמיים בת"ל, ולכן היא לא לכסינה. סתירה.
וקטורים עצמיים בת"ל, ולכן היא לא לכסינה. סתירה.
3. הפותר: עדן קופרווסר
אנחנו מעל המרוכבים, ולכן  דומה למטריצה משולשית
דומה למטריצה משולשית 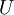 שבאלכסון שלה נמצאים הע"ע של
שבאלכסון שלה נמצאים הע"ע של  . לכן
. לכן 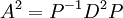 כלומר הע"ע של
כלומר הע"ע של 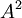 הם בדיוק הריבועים של הע"ע של
הם בדיוק הריבועים של הע"ע של  .
.
נוכיח שהמרחב העצמי של 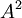 עבור הע"ע
עבור הע"ע 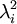 (נסמן אותו ב
(נסמן אותו ב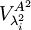 ), שווה לסכום המרחבים העצמיים של
), שווה לסכום המרחבים העצמיים של  עבור הע"ע
עבור הע"ע 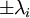 (נסמן אותם ב
(נסמן אותם ב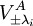 . כלומר נוכיח ש
. כלומר נוכיח ש 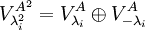 .
.
דבר ראשון נראה שהסכום הוא אכן ישר. נניח 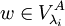 אזי
אזי 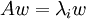 וגם
וגם 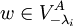 אזי
אזי 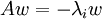 לכן ההפרש בינהם יוצא
לכן ההפרש בינהם יוצא 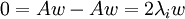 . כעת, נתון ש
. כעת, נתון ש לא הפיכה ולכן 0 לא ע"ע שלה. ולכן
לא הפיכה ולכן 0 לא ע"ע שלה. ולכן 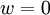 כלומר הסכום הוא ישר.
כלומר הסכום הוא ישר.
דבר שני, נראה הכלה בכיוון ראשון. נניח 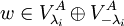 אזי
אזי 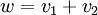 כך ש
כך ש 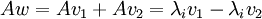 ונכפול שוב במטריצה לקבל
ונכפול שוב במטריצה לקבל 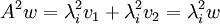 ולכן
ולכן 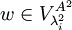 . ולכן
. ולכן 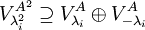 .
.
בכיוון ההפוך, נניח 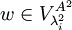 לכן
לכן 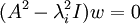 לכן
לכן 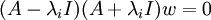 וגם
וגם 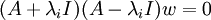 . אם
. אם 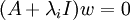 אזי
אזי 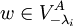 וסיימנו. אם
וסיימנו. אם 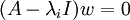 אזי
אזי 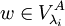 וסיימנו.
וסיימנו.
אם שתי האופציות לא נכונות, כלומר 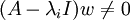 וגם
וגם 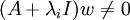 אזי נסמן
אזי נסמן 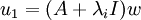 ונסמן
ונסמן 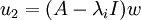 .
.
מהמשוואות למעלה רואים ש 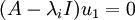 וגם
וגם 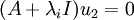 . לכן הם שייכים למרחבים העצמיים המתאימים של
. לכן הם שייכים למרחבים העצמיים המתאימים של  ולכן
ולכן 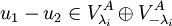 . אבל
. אבל 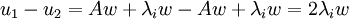 ולכן
ולכן 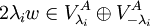 ולכן
ולכן 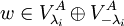 ולכן
ולכן 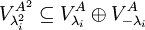 .
.
מכיוון שהראנו הכלה דו-כיוונית אזי 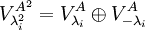 כפי שרצינו להוכיח.
כפי שרצינו להוכיח.
כעת, 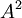 לסכינה, ולכן סכום הריבויים הגיאומטרים של הע"ע שלה שווה
לסכינה, ולכן סכום הריבויים הגיאומטרים של הע"ע שלה שווה  . אבל הריבוי הגיאומטרי זה מימד המרחב העצמי, ולכן
. אבל הריבוי הגיאומטרי זה מימד המרחב העצמי, ולכן 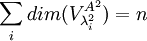 אבל זה שווה
אבל זה שווה ![n=\sum_idim(V_{\lambda_i^2}^{A^2})=\sum_i[dim(V_{\lambda_i}^A)+dim(V_{-\lambda_i}^A)]](/images/math/c/3/f/c3fac60d3e8ad7473b16dceaf2399fbc.png) אבל זה בדיוק סכום הריבויים הגיאומטריים של
אבל זה בדיוק סכום הריבויים הגיאומטריים של  , ויצא לנו שהוא גם כן שווה
, ויצא לנו שהוא גם כן שווה  . ולכן
. ולכן  לכסינה.
לכסינה.