פתרון אינפי 1, תשס"ג, מועד ב,
(המבחן )
חלק א
1) נכון. זאת ההגדרה.
2) נכון. נתבונן בסדרת הסכומים החלקיים: כיון שהטור חיובי היא עולה במובן החלש (אינדוקציה טריויאלית - מוסיפים אברים אי-שליליים). נתון שהיא חסומה. סדרה זאת היא חסומה ומונוטונית ולכן מתכנסת, ולכן הטור מתכנס על-פי הגדרה.
3)
- הוכחה
יהי 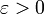 .
.
![\begin{align}\lim_{n\to\infty}\Big[a_n+b_n\Big]=a+b\ \Rightarrow\ \exists N_1\in\N:\forall n>N_1\to\Big|a_n+b_n-(a+b)\Big|<\varepsilon\\\lim_{n\to\infty}\Big[a_n-b_n\Big]=a-b\ \Rightarrow\ \exists N_2\in\N:\forall n>N_2\to\Big|a_n-b_n-(a-b)\Big|<\varepsilon\end{align}](/images/math/d/9/8/d9863870b8e9fb7d7d2439becf2b3408.png)
נגדיר: 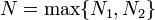 .
.
אז לכל 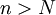 מתקיים
מתקיים
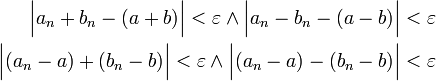
נחבר את שני אי-השוויונות: 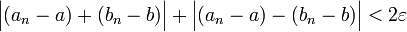
אבל לפי אי-שוויון המשולש
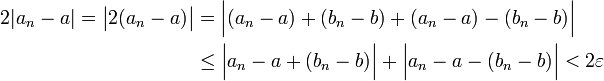
נצמצם ב-2 ונקבל 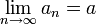 . כעת נחסר את המשוואות במקום לחבר, ונקבל באותו האופן עבור
. כעת נחסר את המשוואות במקום לחבר, ונקבל באותו האופן עבור 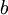 .
.
מש"ל! (התרגיל הזה והתרגיל הבא די יפים :))
- דרך טיפה יותר אלגנטית
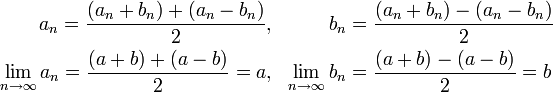
4)
- הוכחה
הטור מתכנס לפי הנתון ל-0. ע"י שינוי סדר אברים ניתן לשנות את הסכום, ולכן הטור מתכנס בתנאי (הוכחנו שלטורים מתכנסים בהחלט שינוי לא משפיע על הסכום). לפי משפט רימאן אכן קיים טור כדרוש.
5) הטענה נכונה. הוכחה: יהי 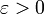 (התחלה מקורית).
(התחלה מקורית).
מהנתון על  נובע
נובע 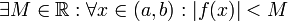 .
.
מהנתון על 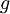 נובע
נובע 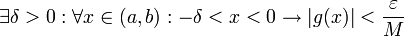 .
.
כעת, עבור 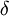 הנ"ל,
הנ"ל, 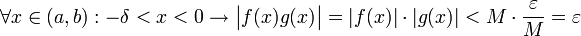 , כנדרש.
, כנדרש.
6)
- הוכחה
רוצים להראות שהפונקציה 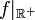 היא על. (זה שילוב סימנים מאינפי, בדידה ולינארית... XD)
היא על. (זה שילוב סימנים מאינפי, בדידה ולינארית... XD)
יהי 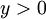 . נגדיר
. נגדיר 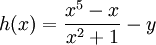 .
.
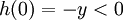 , ואילו מכיון ש-
, ואילו מכיון ש- 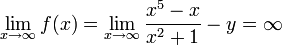 , קיימת נקודה
, קיימת נקודה 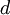 עבורה
עבורה 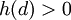 . לפי משפט ערך הביניים קיימת נקודה
. לפי משפט ערך הביניים קיימת נקודה 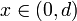 עבורה
עבורה 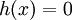 , כלומר
, כלומר 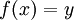 !
!
7) הפרכה: נתבונן בפונקציה 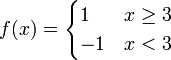 בקטע
בקטע 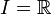 .
.
ברור כי  אינה רציפה ב-3, משום שהגבולות החד-צדדיים שונים, אבל
אינה רציפה ב-3, משום שהגבולות החד-צדדיים שונים, אבל 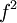 היא קבועה ולכן רציפה בכל הישר הממשי.
היא קבועה ולכן רציפה בכל הישר הממשי.
8)
- הוכחה
כיון שנתון כי 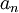 חיובית, גם
חיובית, גם 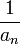 חיובית. נפעיל את מבחן קושי הגבולי על הטור המבוקש: מתקיים
חיובית. נפעיל את מבחן קושי הגבולי על הטור המבוקש: מתקיים
![\displaystyle\lim_{n\to\infty}\sqrt[n]{a_n}>1\Rightarrow\lim_{n\to\infty}\sqrt[n]{\frac{1}{a_n}}<1](/images/math/0/8/6/086a3619fecadc32b04fbeb7cec694bb.png) ולכן הטור המבוקש מתכנס :)
ולכן הטור המבוקש מתכנס :)
חלק ב'
9)
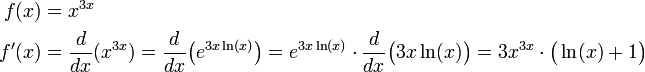
נציב את הנקודה הנתונה למציאת השיפוע: 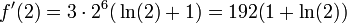 .
.
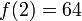 . נציב בנוסחה למשוואת ישר עפ"י נקודה ושיפוע, ונקבל:
. נציב בנוסחה למשוואת ישר עפ"י נקודה ושיפוע, ונקבל:
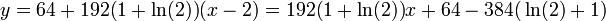 .
.
10) נראה שהטור מתבדר. ברור שהטור הנתון שווה 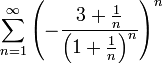 .
.
נבדוק התכנסות בהחלט: לפי מבחן קושי - צריך לבדוק את הגבול העליון של 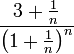 .
.
מתקיים 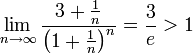 , ולכן הטור אינו מתכנס בהחלט. יתרה מזאת, הטור המקורי מתבדר לפי התוצאה שהוכחנו על מבחן קושי (ראה פתרון מבחן קודם).
, ולכן הטור אינו מתכנס בהחלט. יתרה מזאת, הטור המקורי מתבדר לפי התוצאה שהוכחנו על מבחן קושי (ראה פתרון מבחן קודם).
11) השאלה אמנם נראית מפחידה, אבל זה בסך הכל כלל השרשרת: ניזכר בנוסחה - 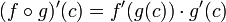
לכן הנגזרת המבוקשת היא
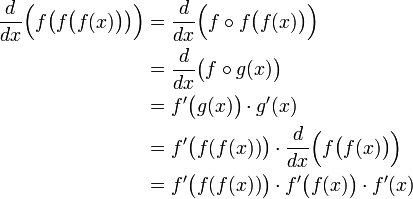
נציב את הנקודה הנתונה: 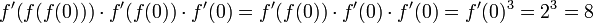 .
.
דוגמא פשוטה היא 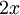 .
.
חלק ג'
12) לפי משפט בולצאנו-ויירשטראס יש ל- 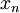 תת-סדרה מתכנסת
תת-סדרה מתכנסת 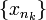 . נסמן את גבולה
. נסמן את גבולה 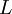 .
.
היא מקיימת את הדרוש, שכן
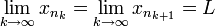
ולכן לפי אריתמטיקת גבולות מתקיים
![\lim_{k\to\infty}\Big[x_{n_{k+1}}-x_{n_k}\Big]=L-L=0](/images/math/1/9/f/19f11eb8ad777feaa7fddbdbff4c6aea.png) כנדרש.
כנדרש.
13) היה בשיעורי הבית. (מניחים בשלילה, משפט ערך הביניים וצפיפות המספרים הממשיים)
14 זלצמן וינץ)
- הוכחה
ידוע שהרכבת פונקציות רבמ"ש בקטע היא רבמ"ש באותו קטע.
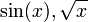 הן רציפות במ"ש בקטע הנתון (סינוס מחזורית, שורש הוכחנו בתרגול) ולכן גם ההרכבה
הן רציפות במ"ש בקטע הנתון (סינוס מחזורית, שורש הוכחנו בתרגול) ולכן גם ההרכבה 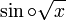 רבמ"ש.
רבמ"ש.
14 אגרנובסקי, דונין והורוביץ) נתבונן בפונקציות 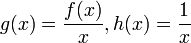 .
.
מתקיים: 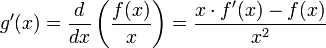 וגם
וגם 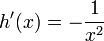 .
.
כעת, נפעיל את משפט הערך הממוצע המוכלל:
קיימת נקודה 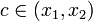 עבורה מתקיים
עבורה מתקיים 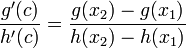 .
.
נפשט את שני אגפי השוויון הקודם: 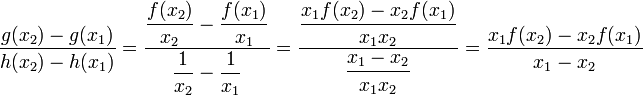
ובאגף השני - 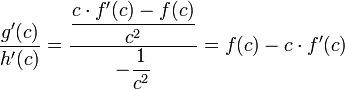
ובסך הכל קיבלנו את הדרוש: