פתרון לינארית 2, אונ' בר אילן, תשנ"ט, מועד א, שאלה 5
הערה התחלתית: דרך ממש קצרה לפתרון: התשובה באופן כללי היא המכפלה של כל הinteger partitions של המעריכים שבפ"א. כאן פונקציית החלוקה של 1 היא 1, של 3=3. לכן התשובה היא 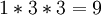 .
.
הסבר מפורט יותר: כל מה שהפ״א קובע זה סכום הסדרים של כל הבלוקים שמתאימים לכל ע״ע.
נסתכל על ע״ע מסויים; החזקה המתאימה לו בפ״א היא סכום גדלי הבלוקים המתאימים לו, וע״י פ״מ שונים ניתן לקבל כל חלוקה לשלמים של הסכום הזה. מספר החלוקות האפשריות האלה הוא מספר הסידורים האפשריים בצורת ז׳ורדן של בלוקים המתאימים לע״ע הזה. (למשל, אם החזקה היא 3 אז אפשר לקבל 1)3 בלוקים מסדר 1, 2)בלוק מסדר 2 ובלוק מסדר1, 3) בלוק יחיד מסדר 3. סה״כ 3 אפשרויות)
לפי עקרון הכפל, כדי למצוא את מס׳ האפשרויות עבור צורת ז׳ורדן כולה יש להכפיל את מס׳ האפשרויות הנדרשות עבור כל ע״ע.
בשיטה זאת נפתר בקלות גם תרגיל 8 במבחן הדוגמא של אותה השנה - מס׳ הצורות הכולל הוא 5*2=10.
מכיוון שזה פתרון לא סטנדרטי, בלשון המעטה, מובא לפניכם פתרון שהוא אולי משעמם לקריאה, אבל משעמם פי כמה לכתיבה :)
(לאוהד החשבתם דרך אחרת לפתרון כפתרון נוסף - Just saying)
סימון - 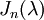 בלוק ז'ורדן המתאים לע"ע
בלוק ז'ורדן המתאים לע"ע  מסדר
מסדר 
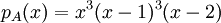
הפ"מ מחלק את הפ"א, ולכן ישנן 9 אפשרויות עבור הפ"מ (באופן כללי - מס' הפ"מ האפשריים בהינתן פ"א הוא כפל כל המעריכים שבפ"א - קומבינטוריקה פשוטה).
מדובר בבדיקה מייגעת ולא מתוחכמת, אבל כנראה שאין ברירה -- נבדוק את כל האפשרויות.
נזכור ראשית שהחזקה של הגורם 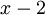 בפולינום המינימלי של A = גודל הבלוק הגדול ביותר המתאים לע"ע 2 בצורת ז'ורדן של המטריצה = 1; לכן מופיע בלוק ז'ורדן של 2 מסדר 1.
אבל הריבוי האלגברי של הע"ע 2 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 2 בצורת ז'ורדן=1, ולכן בכל צורות ז'ורדן האפשריות יש בדיוק בלוק אחד שמתאים ל-2, והוא מסדר 1.
בפולינום המינימלי של A = גודל הבלוק הגדול ביותר המתאים לע"ע 2 בצורת ז'ורדן של המטריצה = 1; לכן מופיע בלוק ז'ורדן של 2 מסדר 1.
אבל הריבוי האלגברי של הע"ע 2 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 2 בצורת ז'ורדן=1, ולכן בכל צורות ז'ורדן האפשריות יש בדיוק בלוק אחד שמתאים ל-2, והוא מסדר 1.
באופן דומה הריבוי האלגברי של הע"ע 1 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 1 בצורת ז'ורדן=3, ו-
הריבוי האלגברי של הע"ע 0 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 0 בצורת ז'ורדן=3.
כעת, עבור כל פ"מ, נמקם ראשית את 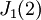 בצורת הז'ורדן, ואז נוכל להתעלם מהע"ע 2, שכן
בצורת הז'ורדן, ואז נוכל להתעלם מהע"ע 2, שכן 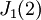 חייב להיות המופע היחיד של הע"ע 2 בצורת ז'ורדן (כי סכום גדלי הבלוקים המתאימים לע"ע 2 צריך להיות 1=המעריך המתאים בפ"א, כפי שכבר פירטתי), ונשים בכל פעם את הבלוקים שחייבים להופיע לפי החזקה המתאימה בפ"מ, ונראה כמה חופש בחירה נותר לנו.
חייב להיות המופע היחיד של הע"ע 2 בצורת ז'ורדן (כי סכום גדלי הבלוקים המתאימים לע"ע 2 צריך להיות 1=המעריך המתאים בפ"א, כפי שכבר פירטתי), ונשים בכל פעם את הבלוקים שחייבים להופיע לפי החזקה המתאימה בפ"מ, ונראה כמה חופש בחירה נותר לנו.
1) עבור פ"מ 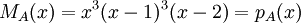 , צורת ז'ורדן נקבעת באופן יחיד.
הרי אנו יודעים שבצורת ז'ורדן חייב להופיע בלוק המתאים לע"ע i, מסדר השווה לחזקה שלו בפ"מ - ונקבל שהמטר' שקיבלנו ע"י הכנסת הבלוקים שחייבים להופיע היא כבר מסדר
, צורת ז'ורדן נקבעת באופן יחיד.
הרי אנו יודעים שבצורת ז'ורדן חייב להופיע בלוק המתאים לע"ע i, מסדר השווה לחזקה שלו בפ"מ - ונקבל שהמטר' שקיבלנו ע"י הכנסת הבלוקים שחייבים להופיע היא כבר מסדר 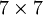 , ולכן היא צורת ז'ורדן. צורת ז'ורדן היא
, ולכן היא צורת ז'ורדן. צורת ז'ורדן היא 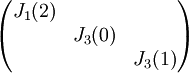 .
.
2) עבור פ"מ 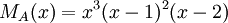 , צורת ז'ורדן נקבעת באופן יחיד.
, צורת ז'ורדן נקבעת באופן יחיד.
צורת ז'ורדן היא 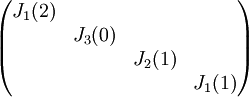
3) עבור פ"מ 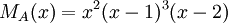 , צורת ז'ורדן נקבעת באופן יחיד.
, צורת ז'ורדן נקבעת באופן יחיד.
צורת ז'ורדן היא 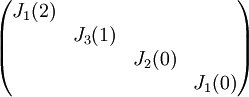
4) עבור פ"מ 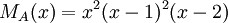 , צורת ז'ורדן נקבעת באופן יחיד.
, צורת ז'ורדן נקבעת באופן יחיד.
צורת ז'ורדן היא 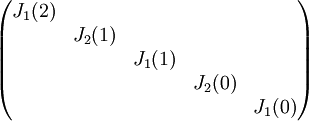
5) עבור פ"מ 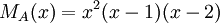 , צורת ז'ורדן נקבעת באופן יחיד.
, צורת ז'ורדן נקבעת באופן יחיד.
צורת ז'ורדן היא 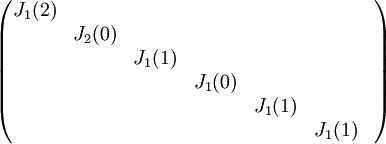
6) עבור פ"מ 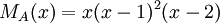 , צורת ז'ורדן נקבעת באופן יחיד.
, צורת ז'ורדן נקבעת באופן יחיד.
צורת ז'ורדן היא 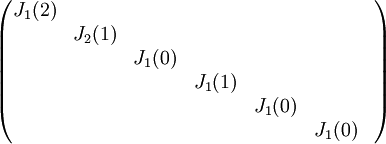
בכך ענינו על סעיף ב'.
7) עבור פ"מ 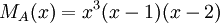 , צורת ז'ורדן נקבעת באופן יחיד.
, צורת ז'ורדן נקבעת באופן יחיד.
צורת ז'ורדן היא 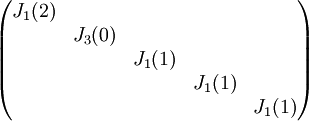
8) עבור פ"מ 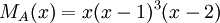 , צורת ז'ורדן נקבעת באופן יחיד.
, צורת ז'ורדן נקבעת באופן יחיד.
צורת ז'ורדן היא 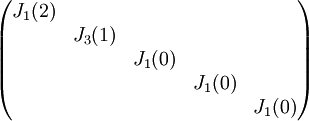
9) לבסוף, עבור הפ"מ 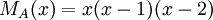 , צורת ז'ורדן נקבעת באופן יחיד, שכן כל הבלוקים הם מסדר 1, והרי המספר של הבלוקים המתאימים לכל ע"ע נקבע חד-משמעית ע"י הפ"א.
, צורת ז'ורדן נקבעת באופן יחיד, שכן כל הבלוקים הם מסדר 1, והרי המספר של הבלוקים המתאימים לכל ע"ע נקבע חד-משמעית ע"י הפ"א.
צורת ז'ורדן היא 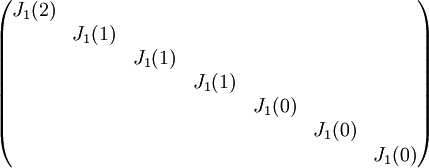
כלומר, לכל אחת מ-9 האפשרויות יש בדיוק צורת ז'ורדן אפשרית אחת. לכן יש
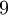 צורות ז'ורדן אפשריות בסה"כ!
צורות ז'ורדן אפשריות בסה"כ!
מש"ל.
הערות: 1) בפתרון הנחתי שצורת ז'ורדן שמתקבלת מסדר שונה של הבלוקים באלכסון היא זהה. (זה בסדר כי הן דומות; אם רוצים דווקא להחשיב אותן בנפרד, צריך להכפיל את האפשרויות שבכל מקרה ב(עצרת של (מס' הבלוקים שבצורת ז'ורדן)))
לכן בכל מקום שבו כתוב 'יחיד/ה' על צורת ז'ורדן, הכוונה היא עד כדי שינוי סדר הבלוקים.
2)כאשר במטריצה לא מופיעים במפורש איברים - המקומות החסרים הם אפסים.