הבדלים בין גרסאות בדף "פתרון לינארית 2, אונ' בר אילן, תשנ"ט, מועד א, שאלה 5"

גרסה מ־19:59, 19 בדצמבר 2011

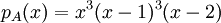
$p_A(x)=x^{3}(x-1)^{3}(x-2)$

הפ"מ מחלק את הפ"א, ולכן ישנן 9 אפשרויות עבור הפ"מ (באופן כללי - מס' הפ"מ האפשריים הוא כפל כל המעריכים שבפ"א - קומבינטוריקה פשוטה). מדובר בבדיקה מייגעת ולא מתוחכמת, אבל כנראה שאין ברירה -- נבדוק את כל האפשרויות.

נזכור ראשית שהחזקה של הגורם 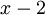$\ x-2$ בפולינום המינימלי של A = גודל הבלוק הגדול ביותר המתאים לע"ע 2 בצורת ז'ורדן של המטריצה = 1; לכן מופיע בלוק ז'ורדן של 2 מסדר 1. אבל הריבוי האלגברי של הע"ע 2 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 2 בצורת ז'ורדן=1, ולכן בכל צורות ז'ורדן האפשריות יש בדיוק בלוק אחד שמתאים ל-2, והוא מסדר 1.

באופן דומה הריבוי האלגברי של הע"ע 0 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 0 בצורת ז'ורדן=3, ו- הריבוי האלגברי של הע"ע 3 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 3 בצורת ז'ורדן=3.

כעת, עבור כל פ"מ, נמקם ראשית את 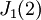$J_1(2)$ בצורת הז'ורדן, ואז נוכל להתעלם מהע"ע 2, ונשים בכל פעם את הבלוקים שחייבים להופיע לפי החזקה המתאימה בפ"מ, ונראה כמה חופש בחירה נותר לנו.

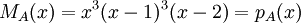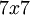1) עבור פ"מ $M_A(x)=x^{3}(x-1)^{3}(x-2)=p_A(x)$ , צורת ז'ורדן נקבעת באופן יחיד. הרי אנו יודעים שבצורת ז'ורדן חייב להופיע בלוק המתאים לע"ע i, מסדר השווה לחזקה שלו בפ"מ - ונקבל שהמטר' שקיבלנו היא כבר מסדר $7x7$ , ולכן היא צורת ז'ורדן.

2) עבור פ"מ 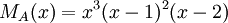$M_A(x)=x^{3}(x-1)^{2}(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

3) עבור פ"מ 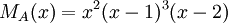$M_A(x)=x^{2}(x-1)^{3}(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

4) עבור פ"מ 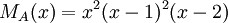$M_A(x)=x^{2}(x-1)^{2}(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

5) עבור פ"מ 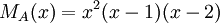$M_A(x)=x^{2}(x-1)(x-2)$ , ישנן 2 אפשרויות לצורות ז'ורדן: השוני ביניהן הוא בבלוקים המתאימים לע"ע 1.

6) עבור פ"מ 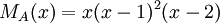$M_A(x)=x(x-1)^{2}(x-2)$ , ישנן 2 אפשרויות לצורות ז'ורדן: השוני ביניהן הוא בבלוקים המתאימים לע"ע 0. בכך ענינו על סעיף ב'.

7) עבור פ"מ 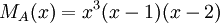$M_A(x)=x^{3}(x-1)(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

8) עבור פ"מ 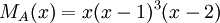$M_A(x)=x(x-1)^{3}(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד.

9) לבסוף, עבור הפ"מ 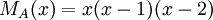$M_A(x)=x(x-1)(x-2)$ , צורת ז'ורדן נקבעת באופן יחיד, שכן כל הבלוקים הם מסדר 1, והרי המספר של הבלוקים המתאימים לכל ע"ע נקבע חד-משמעית ע"י הפ"א.

נותר רק לסכם את המספרים שקיבלנו (ולהוסיף פירוט אם המרצים יבקשו, אבל זה באמת תהליך רפטטיבי), ולקבל 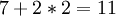$7+2*2=11$ צורות ז'ורדן אפשריות!

@@ שורה 6: / שורה 6: @@
 נזכור ראשית שהחזקה של הגורם <math>\ x-2</math> בפולינום המינימלי של A = גודל הבלוק הגדול ביותר המתאים לע"ע 2 בצורת ז'ורדן של המטריצה = 1; לכן מופיע בלוק ז'ורדן של 2 מסדר 1.
 אבל הריבוי האלגברי של הע"ע 2 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 2 בצורת ז'ורדן=1, ולכן בכל צורות ז'ורדן האפשריות יש בדיוק בלוק אחד שמתאים ל-2, והוא מסדר 1.
 באופן דומה הריבוי האלגברי של הע"ע 0 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 0 בצורת ז'ורדן=3, ו-
 הריבוי האלגברי של הע"ע 3 בפולינום האופייני = סכום הגדלים של הבלוקים המתאימים ל- 3 בצורת ז'ורדן=3.
 כעת, עבור כל פ"מ, נמקם ראשית את <math>J_1(2)</math> בצורת הז'ורדן, ואז נוכל להתעלם מהע"ע 2, ונשים בכל פעם את הבלוקים שחייבים להופיע לפי החזקה המתאימה בפ"מ, ונראה כמה חופש בחירה נותר לנו.
 ) עבור פ"מ <math>M_A(x)=x^{3}(x-1)^{3}(x-2)=p_A(x)</math>, צורת ז'ורדן נקבעת באופן יחיד.
 הרי אנו יודעים שבצורת ז'ורדן חייב להופיע בלוק המתאים לע"ע i, מסדר השווה לחזקה שלו בפ"מ - ונקבל שהמטר' שקיבלנו היא כבר מסדר <math>7x7</math>, ולכן היא צורת ז'ורדן.
 ) עבור פ"מ <math>M_A(x)=x^{3}(x-1)^{2}(x-2)</math>, צורת ז'ורדן נקבעת באופן יחיד.
 ) עבור פ"מ <math>M_A(x)=x^{2}(x-1)^{3}(x-2)</math>, צורת ז'ורדן נקבעת באופן יחיד.
 ) עבור פ"מ <math>M_A(x)=x^{2}(x-1)^{2}(x-2)</math>, צורת ז'ורדן נקבעת באופן יחיד.
 ) עבור פ"מ <math>M_A(x)=x^{2}(x-1)(x-2)</math>, ישנן 2 אפשרויות לצורות ז'ורדן: השוני ביניהן הוא בבלוקים המתאימים לע"ע 1.
 ) עבור פ"מ <math>M_A(x)=x(x-1)^{2}(x-2)</math>, ישנן 2 אפשרויות לצורות ז'ורדן: השוני ביניהן הוא בבלוקים המתאימים לע"ע 0.
 בכך ענינו על סעיף ב'.
 ) עבור פ"מ <math>M_A(x)=x^{3}(x-1)(x-2)</math>, צורת ז'ורדן נקבעת באופן יחיד.
 ) עבור פ"מ <math>M_A(x)=x(x-1)^{3}(x-2)</math>, צורת ז'ורדן נקבעת באופן יחיד.
 ) לבסוף, עבור הפ"מ <math>M_A(x)=x(x-1)(x-2)</math>,  צורת ז'ורדן נקבעת באופן יחיד, שכן כל הבלוקים הם מסדר 1, והרי המספר של הבלוקים המתאימים לכל ע"ע נקבע חד-משמעית ע"י הפ"א.

הבדלים בין גרסאות בדף "פתרון לינארית 2, אונ' בר אילן, תשנ"ט, מועד א, שאלה 5"

גרסה מ־19:59, 19 בדצמבר 2011

תפריט הניווט

כלים אישיים

גרסאות שפה

מרחבי שם

חיפוש

עוד

צפיות

ניווט

כלים