שיחה:הסודות של גוגל
מתוך Math-Wiki
3.3
שאלת תלמיד: בהוכחה אפשר לקחת באופן מפורש
![\epsilon=\frac{1}{2}min\left \{ [A\cdot |v|]_{i} \right \}_{1 \leq i\leq n }](/images/math/4/5/f/45ffa099043357e9c8b18150d2c8669d.png) , נכון? (כאשר
, נכון? (כאשר 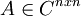 )
)
תשובה: הרבה יותר קל לחשוב קונספטואלית (בלי חישובים): נתונים שני וקטורים, האחד חיובי והשני אי-שלילי. ניקח את האיבר הקטן
ביותר של הוקטור החיובי, נניח שהוא 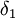 . ניקח את האיבר הגדול ביותר של הוקטור האי-שלילי, נקרא לו
. ניקח את האיבר הגדול ביותר של הוקטור האי-שלילי, נקרא לו
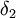 . ברור שיש
. ברור שיש 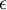 כך ש
כך ש
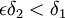 ,
וממילא כל רכיבי הוקטור השני, אחרי שנכפילם ב
,
וממילא כל רכיבי הוקטור השני, אחרי שנכפילם ב 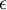 , יהיו קטנים יותר מכל רכיבי הוקטור הראשון.
, יהיו קטנים יותר מכל רכיבי הוקטור הראשון.
אם אתה מתעקש על משהו של ממש, ניקח למשל 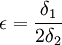 , ואם
, ואם 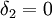 אז ניקח למשל
אז ניקח למשל 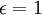 .
.
(קיבצתי כאן שאלות שלי בנושא שנותרו בלא מענה בדף השאלות והתשובות.)
נורמת אינסוף
באילו תנאים מתקיים 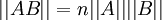 ?
(מה ניתן להסיק אם זה מתקיים?)
?
(מה ניתן להסיק אם זה מתקיים?)
נורמת אינסוף 2
האם יש מ״פ על 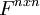
כך שנורמת אינסוף היא הנורמה המושרית שלה? אם לא, איך מראים את זה?
- כל נורמה המושרית על-ידי מכפלה פנימית מקיימת את שוויון המקבילית (וגם להיפך). כדי להראות שנורמה מסויימת אינה מושרית על-ידי מכפלה פנימית, מספיק להראות שהיא אינה מקיימת את שוויון המקבילית. עוזי ו. 01:30, 1 במרץ 2012 (IST)