הבדלים בין גרסאות בדף "תרגילי חובה לא סטנדרטיים"

גרסה מ־12:32, 19 בדצמבר 2016

תרגילים שעלולים לשכוח ולא כדאי:

חשבון במשתנה ממשי יחיד

אי-שוויון הממוצעים
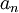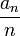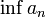הלמה של פקטה: אם $a_n$ סדרה תת-אדיטיבית, אז ל- $\frac{a_n}{n}$ יש גבול במובן הרחב השווה ל $\inf a_n$ ).
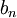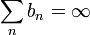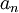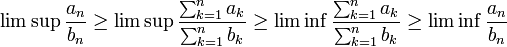
המשפט של Stolz-Cesàro: אם $b_n$ סידרה חיובית כך ש $\sum_n b_n=\infty$ אז לכל סידרה $a_n$ , $\limsup \frac{a_n}{b_n}\ge\limsup\frac{\sum_{k=1}^n a_k}{\sum_{k=1}^n b_k}\ge\liminf \frac{\sum_{k=1}^n a_k}{\sum_{k=1}^n b_k}\ge \liminf \frac{a_n}{b_n}$
ממוצע אריתמטי, גאומטרי, והרמוני.
סומביליות Cesàro: לכל סדרה מתכנסת גם סדרת הממוצעים החשובניים מתכנסת ולאותו ערך, אבל יש סדרות שהממוצעים שלהן מתכנסים אולם הן לא.
סומביליות Abel: (אם הסכום 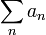$\sum_n a_n$ קיים אז גם 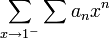$\sum_{x\to 1^-} \sum a_n x^n$ קיים ושווה לו; אבל יש טורים שאינם מתכנסים אלא באופן זה).
קירוב סטירלינג.
הלמה של Reimann-Lebesgue.

יש אינסוף ראשוניים. יש אינסוף ראשוניים מהצורה 4n-1. יש אינסוף ראשוניים מהצורה 4n+1.

@@ שורה 10: / שורה 10: @@
 '''חשבון במשתנה ממשי יחיד'''
 * אי-שוויון הממוצעים
-* הלמה של פקטה: אם <math>a_n</math> סדרה תת-אדיטיבית, אז ל-<math>a_n/n</math> יש גבול במובן הרחב השווה ל<math>\inf a_n</math>).
+* הלמה של פקטה: אם <math>a_n</math> סדרה תת-אדיטיבית, אז ל-<math>\frac{a_n}{n}</math> יש גבול במובן הרחב השווה ל<math>\inf a_n</math>).
 * המשפט של Stolz-Cesàro: אם <math>b_n</math> סידרה חיובית כך ש<math>\sum_n b_n=\infty</math> אז לכל סידרה <math>a_n</math>, <math>\limsup \frac{a_n}{b_n}\ge\limsup\frac{\sum_{k=1}^n a_k}{\sum_{k=1}^n b_k}\ge\liminf \frac{\sum_{k=1}^n a_k}{\sum_{k=1}^n b_k}\ge \liminf \frac{a_n}{b_n}</math>
 * ממוצע אריתמטי, גאומטרי, והרמוני.