88-132 אינפי 1 סמסטר א' תשעב/מדמח/פתרון בוחן 2
תוכן עניינים
1
תנאי הכרחי להתכנסות הטור 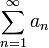 הוא התכנסות הסדרה
הוא התכנסות הסדרה 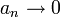 . תנאי זה הכרחי אבל אינו מספיק.
. תנאי זה הכרחי אבל אינו מספיק.
טור מתכנס בתנאי הנו טור המתכנס, אבל אינו מתכנס בהחלט.
2
א
ברור כי 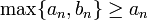 ולכן לפי מבחן ההשוואה הראשון לטורים חיוביים הטור מתבדר.
ולכן לפי מבחן ההשוואה הראשון לטורים חיוביים הטור מתבדר.
ב
כיון שהטור 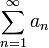 מתכנס, אזי הסדרה שלו שואפת ל-0. לכן
מתכנס, אזי הסדרה שלו שואפת ל-0. לכן
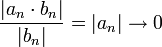
ולכן לפי מבחן ההשוואה השני לטורים חיוביים, הטור 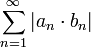 מתכנס, כלומר הטור
מתכנס, כלומר הטור 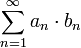 מתכנס בהחלט.
מתכנס בהחלט.
ג
הוכחה:
כיון שהטור 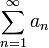 מתכנס, אזי הסדרה שלו שואפת לאפס. לכן הסדרה
מתכנס, אזי הסדרה שלו שואפת לאפס. לכן הסדרה 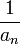 לא חסומה או לא-מוגדרת ובכל מקרה אינה שואפת ל-0 ולכן הטור
לא חסומה או לא-מוגדרת ובכל מקרה אינה שואפת ל-0 ולכן הטור 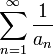 מתבדר.
מתבדר.
ד
הפרכה:
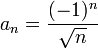 מתכנס לפי לייבניץ, אבל
מתכנס לפי לייבניץ, אבל 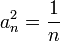 מתבדר.
מתבדר.
3
א
ב
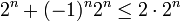
ולכן סה"כ הטור קטן מהטור ההנדסי המתכנס
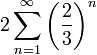
ולכן מתכנס.
ג
ד
ה
נפעיל את מבחן המנה:
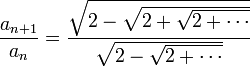
נכפיל בצמוד של המונה למעלה ולמטה לקבל:
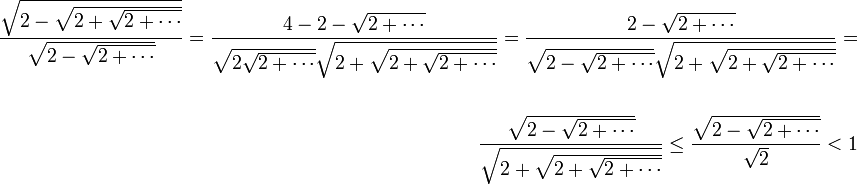
ולכן הטור מתכנס.
4
א
מתכונות פונקציות הקוסינוס ניתן לראות שאנו מקבלים סכום של טורים בעלי סדרה השואפת מונוטונית ל-0 עם סימנים מתחלפים ולכן מתכנס לפי לייבניץ.
ידוע שהטור אינו מתכנס בהחלט, ולכן סה"כ הטור מתכנס בתנאי.
ב
הטור מתבדר שכן סכום אבריו השליליים מתכנס בעוד סכום אבריו החיוביים מתבדר.
ג
הטור מתכנס בהחלט לפי מבחן ההשוואה הראשון עם הטור 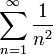 .
.