הבדלים בין גרסאות בדף "88-132 סמסטר א' תשעא/ פתרון מועד א'"
(←שאלה 6) |
יהודה שמחה (שיחה | תרומות) |
||
| (9 גרסאות ביניים של 4 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | [[קטגוריה:פתרון מבחנים]][[קטגוריה:אינפי]] | ||
=המבחן של פרופ' זלצמן= | =המבחן של פרופ' זלצמן= | ||
==שאלה 1== | ==שאלה 1== | ||
| − | הוכח/הפרך: הסדרה a_n מתכנסת אם"ם לכל תת סדרה | + | הוכח/הפרך: הסדרה <math>a_n</math> מתכנסת אם"ם לכל תת-סדרה <math>a_{n_k}</math> יש-תת סדרה מתכנסת. |
| − | + | ;הפרכה | |
| − | כל סדרה חסומה שאינה מתכנסת מהווה דוגמא נגדית, | + | כל סדרה חסומה שאינה מתכנסת מהווה דוגמא נגדית, מכיון שכל תת-סדרה חסומה גם היא ולפי משפט בולצאנו-ויירשטראס יש לה תת-סדרה מתכנסת. (למשל <math>a_n=(-1)^n</math>) |
==שאלה 2== | ==שאלה 2== | ||
| שורה 10: | שורה 11: | ||
===א=== | ===א=== | ||
| − | <math>\ | + | <math>\displaystyle\sum_{n=1}^\infty(-1)^n\frac{2^{n^3}}{(n!)^n}</math> |
| − | נבדוק התכנסות בהחלט, נפעיל מבחן קושי, | + | נבדוק התכנסות בהחלט, נפעיל מבחן קושי, לקבלת: |
| − | <math>b_n=\sqrt[n]{|a_n|}=\ | + | <math>b_n=\sqrt[n]{|a_n|}=\dfrac{2^{n^2}}{n!}</math> |
| − | קל לראות | + | קל לראות כי <math>\dfrac{b_{n+1}}{b_n}\to\infty</math> ולכן <math>b_n\to\infty</math> . לכן <math>|a_n|\to\infty</math> ולכן הטור '''מתבדר לחלוטין'''. |
===ב=== | ===ב=== | ||
| − | <math>\ | + | <math>\displaystyle\sum_{n=1}^\infty(-1)^n\frac{\sin\left(\frac1n\right)}{\log^2(n)}</math> |
| − | נבדוק התכנסות בהחלט. קל לראות | + | נבדוק התכנסות בהחלט. קל לראות כי |
| − | <math>\ | + | <math>\dfrac{\dfrac{\sin\left(\frac1n\right)}{\log^2(n)}}{\dfrac1{n\cdot\log^2(n)}}\to1</math> |
| − | ולכן הטורים חברים. נוכיח שהשני מתכנס בעזרת מבחן העיבוי (מותר כי זו סדרה מונוטונית יורדת | + | ולכן הטורים חברים. נוכיח שהשני מתכנס בעזרת מבחן העיבוי (מותר כי זו סדרה מונוטונית יורדת ל-0): |
| − | <math>\ | + | <math>\dfrac{2^n}{2^n\cdot\log^2(2^n)}=\dfrac1{n^2\cdot\log^2(2)}</math> |
זה קבוע כפול טור שידוע כמתכנס, לכן סה"כ הטור '''מתכנס בהחלט'''. | זה קבוע כפול טור שידוע כמתכנס, לכן סה"כ הטור '''מתכנס בהחלט'''. | ||
===ג=== | ===ג=== | ||
| − | <math>\ | + | <math>\displaystyle\sum_{n=1}^\infty(-\pi)^n\frac{(n!)^2}{(2n)!}</math> |
| − | נבדוק התכנסות בהחלט, נפעיל את מבחן דלאמבר לקבל <math>|\ | + | נבדוק התכנסות בהחלט, נפעיל את מבחן דלאמבר לקבל |
| + | |||
| + | <math>\left|\dfrac{a_{n+1}}{a_n}\right|=\dfrac{\pi^{n+1}\dfrac{\big((n+1)!\big)^2}{\big(2(n+1)\big)!}}{\pi^n\dfrac{(n!)^2}{(2n)!}}=\pi\cdot\dfrac{(n+1)^2}{(2n+1)(2n+2)}=\frac{\pi}{2}\cdot\dfrac{n+1}{2n+1}\to\dfrac{\pi}{4}<1</math> | ||
ולכן הטור '''מתכנס בהחלט'''. | ולכן הטור '''מתכנס בהחלט'''. | ||
==שאלה 4== | ==שאלה 4== | ||
| − | זהה וסווג את נקודות אי הרציפות | + | זהה וסווג את נקודות אי-הרציפות. |
===א=== | ===א=== | ||
| − | <math>e^{-\ | + | <math>e^{-\frac1{x^3}}</math> |
| − | נקודת אי הרציפות היא | + | נקודת אי-הרציפות היא 0. הגבול משמאל הנו <math>\infty</math> ולכן זה '''מין שני'''. |
===ב=== | ===ב=== | ||
| − | <math>\frac{sin(x^2)}{|sin(x^2)|}</math> | + | <math>\frac{\sin(x^2)}{\big|\sin(x^2)\big|}</math> |
| − | כמו שלמדנו, הפונקציה הזו מקבלת | + | כמו שלמדנו, הפונקציה הזו מקבלת 1 כאשר <math>\sin(x^2)</math> חיובי, 1- כאשר הוא שלילי, ב-0 היא לא-מוגדרת ולכן זו נקודת אי-רציפות. לכן סה"כ נקודות אי-הרציפות הנן <math>\pm \sqrt{\pi k}</math> כאשר <math>k\ge0</math> . פרט ל-0, הן כולן '''מין ראשון''' מכיון שמצד אחד הסינוס שלילי, ומהצד השני חיובי (מימין לנקודת אי-הרציפות או משמאלה). |
| − | + | ב-0, אנחנו מתקרבים אליו רק מהצד החיובי שם הסינוס חיובי ולכן הוא נקודת אי-רציפות '''סליקה'''. | |
===ג=== | ===ג=== | ||
<math>f'(x)</math> כאשר <math>f(x)=|x^2-1|</math> | <math>f'(x)</math> כאשר <math>f(x)=|x^2-1|</math> | ||
| − | נחלק לתחומים. בתחום <math>x>1,x<-1</math> | + | נחלק לתחומים. בתחום <math>x>1\ ,\ x<-1</math> מתקיים <math>f(x)=x^2-1</math> ולכן <math>f'(x)=2x</math> . |
| − | בתחום <math>-1<x<1</math> מתקיים <math>f(x)=1-x^2</math> ולכן <math>f'(x)=-2x</math>. | + | בתחום <math>-1<x<1</math> מתקיים <math>f(x)=1-x^2</math> ולכן <math>f'(x)=-2x</math> . |
| − | קל | + | קל אפוא לראות שבנקודות <math>\pm1</math> יש אי-רציפות מ'''מין ראשון''' (שם הנגזרת מתקרבת ל-2 מצד אחד ו-2- מצד שני). |
==שאלה 5== | ==שאלה 5== | ||
| שורה 67: | שורה 70: | ||
===א=== | ===א=== | ||
| − | <math> | + | <math>x\sin\left(\tfrac1{x^2}\right)</math> בתחום <math>(0,\infty)</math> . |
קל לראות שהפונקציה רציפה בקטע, נבדוק גבולות בקצות הקטע: | קל לראות שהפונקציה רציפה בקטע, נבדוק גבולות בקצות הקטע: | ||
| − | <math>\lim_{x\ | + | <math>\lim_{x\to0}x\sin\left(\tfrac1{x^2}\right)=0</math> אפס כפול חסומה |
| − | <math>\lim_{x\ | + | <math>\displaystyle\lim_{x\to\infty}x\sin\left(\frac1{x^2}\right)=\lim_{x\to\infty}\frac1x\cdot\frac{\sin\left(\tfrac1{x^2}\right)}{\frac1{x^2}}=0\cdot1=0</math> |
| − | שני הגבולות סופיים ולכן הפונקציה '''רציפה במ"ש''' | + | שני הגבולות סופיים ולכן הפונקציה '''רציפה במ"ש'''. |
===ב=== | ===ב=== | ||
| − | <math>\ | + | <math>\dfrac1{1+\ln(x)}</math> בתחום <math>(0,\infty)</math> . |
קל לראות שהפונקציה אינה מוגדרת בנקודה <math>e^{-1}</math> שנמצאת בתחום ולכן '''אינה רציפה במ"ש''' שם. | קל לראות שהפונקציה אינה מוגדרת בנקודה <math>e^{-1}</math> שנמצאת בתחום ולכן '''אינה רציפה במ"ש''' שם. | ||
===ג=== | ===ג=== | ||
| − | <math>\sqrt{|cos(\pi x)|}</math> בתחום <math>(-\infty,\infty)</math> | + | <math>\sqrt{\big|\cos(\pi x)\big|}</math> בתחום <math>(-\infty,\infty)</math> . |
| − | זו הרכבה של פונקציה רציפות במ"ש: <math>\sqrt{x},|x|,cos(x),\pi x</math> ולכן '''רציפה במ"ש''' בתחום. | + | זו הרכבה של פונקציה רציפות במ"ש: <math>\sqrt{x},|x|,\cos(x),\pi x</math> ולכן '''רציפה במ"ש''' בתחום. |
==שאלה 7== | ==שאלה 7== | ||
| − | חשב את הקירוב הלינארי של <math>h=g^{-1}\circ f^{-1}</math> ב<math>x_0=2</math>. | + | חשב את הקירוב הלינארי של <math>h=g^{-1}\circ f^{-1}</math> ב- <math>x_0=2</math> . |
| + | |||
| + | הקירוב הלינארי של <math>h(x)</math> באזור הנקודה <math>x_0</math> , הנו <math>h(x_0)+h'(x_0)(x-x_0)</math> | ||
| − | + | במקרה שלנו | |
| − | + | <math>h'(2)=(g^{-1}\circ f^{-1})'(2)=\Big[\dfrac{d}{dx}g^{-1}\Big(f^{-1}(2)\Big)\Big]\cdot\Big[\dfrac{d}{dx}f^{-1}(2)\Big]= | |
| + | \frac{1}{g'\Big(g^{-1}\big(f^{-1}(2)\big)\Big)}\cdot\dfrac1{f'\big(f^{-1}(2)\big)}</math> | ||
| − | ולכן סה"כ <math>h(x)=7-\frac{ | + | ולכן סה"כ <math>h(x)=7-\frac{x-2}{7}</math> |
=המבחן של דר' שמחה הורוביץ= | =המבחן של דר' שמחה הורוביץ= | ||
==שאלה 3== | ==שאלה 3== | ||
| − | תהי g פונקציה רציפה במ"ש בקטע (0,1). נניח שקיים | + | תהי <math>g</math> פונקציה רציפה במ"ש בקטע <math>(0,1)</math> . נניח שקיים <math>\varepsilon>0</math> כך שמתקיים <math>g(x)>\varepsilon</math> לכל <math>x\in(0,1)</math> . הוכח שהפונקציה <math>\dfrac1g</math> רציפה במ"ש בקטע <math>(0,1)</math> . |
| − | + | ;הוכחה | |
| − | לפי הנתון, לכל | + | לפי הנתון, לכל <math>\alpha>0</math> קיים <math>\delta>0</math> כך שאם <math>|x_1-x_2|<\delta</math> מתקיים <math>\Big|g(x_1)-g(x_2)\Big|<\alpha\cdot\varepsilon^2</math> . |
| − | לכן, מתקיים | + | לכן, מתקיים <math>\left|\dfrac1{g(x_1)}-\dfrac1{g(x_2)}\right|=\left|\dfrac{g(x_2)-g(x_1)}{g(x_1)\cdot g(x_2)}\right|<\dfrac{\alpha\cdot\varepsilon^2}{\varepsilon^2}=\alpha</math> |
| − | כפי שרצינו. | + | כפי שרצינו. <math>\blacksquare</math> |
==שאלה 6== | ==שאלה 6== | ||
| − | תהי f פונקציה בעלת חמש נגזרת רציפות על הממשיים. נניח ש <math>f(0)=f'(0)= | + | תהי <math>f</math> פונקציה בעלת חמש נגזרת רציפות על הממשיים. נניח ש- <math>f(0)=f'(0)=\ldots=f^{(4)}(0)=0</math> וגם <math>f^{(5)}(0)>0</math> . עוד נניח שלכל <math>x\ne 0</math> מתקיים <math>f'(x)\ne 0</math> . הוכיחו שלכל <math>x>0</math> מתקיים <math>f(x)>0</math> . |
| − | + | ;הוכחה | |
| − | + | מכיון שהפונקציה ו-4 נגזרותיה מתאפסות ב-0, פולינום טיילור מסדר 4 בסביבת הנקודה <math>x=0</math> שווה זהותית ל-0. השארית היא מהצורה <math>\dfrac{f^{(5)}(c)}{5!}x^5</math> כאשר <math>0<c<x</math> . | |
| − | <math>\ | + | |
| − | + | מכיון ש- <math>f^{(5)}(0)>0</math> והנגזרת החמישית רציפה, אז קיימת סביבה של 0 בה <math>f^{(5)}>0</math> . לכן בסביבה ימנית של 0 מתקיים <math>f(x)=\dfrac{f^{(5)}(c)}{5!}x^5>0</math> . | |
| − | נותר להוכיח | + | נותר להוכיח כי <math>f(x)>0</math> עבור <math>x>0</math> גם מחוץ לסביבה הימנית הזו. נניח בשלילה כי <math>f(x)\le0</math> אזי לפי משפט ערך הביניים <math>f(x)=0</math> עבור <math>x>0</math> כלשהוא. אבל גם <math>f(0)=0</math> ולכן לפי משפט רול הנגזרת מתאפסת עבור נקודה גדולה מ-0, בסתירה. |
גרסה אחרונה מ־15:44, 12 בפברואר 2017
תוכן עניינים
המבחן של פרופ' זלצמן
שאלה 1
הוכח/הפרך: הסדרה 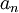 מתכנסת אם"ם לכל תת-סדרה
מתכנסת אם"ם לכל תת-סדרה 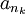 יש-תת סדרה מתכנסת.
יש-תת סדרה מתכנסת.
- הפרכה
כל סדרה חסומה שאינה מתכנסת מהווה דוגמא נגדית, מכיון שכל תת-סדרה חסומה גם היא ולפי משפט בולצאנו-ויירשטראס יש לה תת-סדרה מתכנסת. (למשל 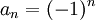 )
)
שאלה 2
בדוק התכנסות של הטורים הבאים:
א
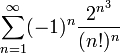
נבדוק התכנסות בהחלט, נפעיל מבחן קושי, לקבלת:
![b_n=\sqrt[n]{|a_n|}=\dfrac{2^{n^2}}{n!}](/images/math/2/6/b/26bf50640949f10a088f92c7f873ef01.png)
קל לראות כי 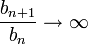 ולכן
ולכן 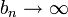 . לכן
. לכן 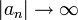 ולכן הטור מתבדר לחלוטין.
ולכן הטור מתבדר לחלוטין.
ב
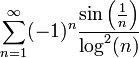
נבדוק התכנסות בהחלט. קל לראות כי
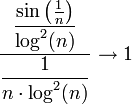
ולכן הטורים חברים. נוכיח שהשני מתכנס בעזרת מבחן העיבוי (מותר כי זו סדרה מונוטונית יורדת ל-0):
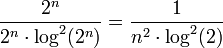
זה קבוע כפול טור שידוע כמתכנס, לכן סה"כ הטור מתכנס בהחלט.
ג
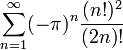
נבדוק התכנסות בהחלט, נפעיל את מבחן דלאמבר לקבל
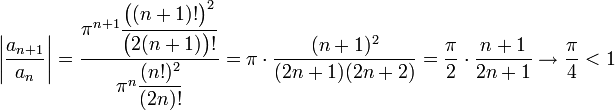
ולכן הטור מתכנס בהחלט.
שאלה 4
זהה וסווג את נקודות אי-הרציפות.
א
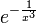
נקודת אי-הרציפות היא 0. הגבול משמאל הנו 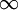 ולכן זה מין שני.
ולכן זה מין שני.
ב
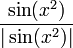
כמו שלמדנו, הפונקציה הזו מקבלת 1 כאשר 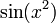 חיובי, 1- כאשר הוא שלילי, ב-0 היא לא-מוגדרת ולכן זו נקודת אי-רציפות. לכן סה"כ נקודות אי-הרציפות הנן
חיובי, 1- כאשר הוא שלילי, ב-0 היא לא-מוגדרת ולכן זו נקודת אי-רציפות. לכן סה"כ נקודות אי-הרציפות הנן 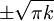 כאשר
כאשר 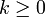 . פרט ל-0, הן כולן מין ראשון מכיון שמצד אחד הסינוס שלילי, ומהצד השני חיובי (מימין לנקודת אי-הרציפות או משמאלה).
. פרט ל-0, הן כולן מין ראשון מכיון שמצד אחד הסינוס שלילי, ומהצד השני חיובי (מימין לנקודת אי-הרציפות או משמאלה).
ב-0, אנחנו מתקרבים אליו רק מהצד החיובי שם הסינוס חיובי ולכן הוא נקודת אי-רציפות סליקה.
ג
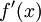 כאשר
כאשר 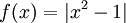
נחלק לתחומים. בתחום 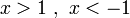 מתקיים
מתקיים 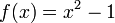 ולכן
ולכן 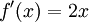 .
.
בתחום 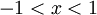 מתקיים
מתקיים 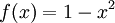 ולכן
ולכן 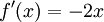 .
.
קל אפוא לראות שבנקודות 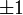 יש אי-רציפות ממין ראשון (שם הנגזרת מתקרבת ל-2 מצד אחד ו-2- מצד שני).
יש אי-רציפות ממין ראשון (שם הנגזרת מתקרבת ל-2 מצד אחד ו-2- מצד שני).
שאלה 5
אילו מהפונקציות הבאות רציפות במ"ש בקטעים המסומנים?
א
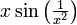 בתחום
בתחום 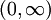 .
.
קל לראות שהפונקציה רציפה בקטע, נבדוק גבולות בקצות הקטע:
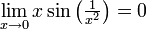 אפס כפול חסומה
אפס כפול חסומה
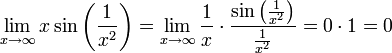
שני הגבולות סופיים ולכן הפונקציה רציפה במ"ש.
ב
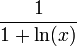 בתחום
בתחום 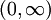 .
.
קל לראות שהפונקציה אינה מוגדרת בנקודה 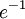 שנמצאת בתחום ולכן אינה רציפה במ"ש שם.
שנמצאת בתחום ולכן אינה רציפה במ"ש שם.
ג
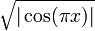 בתחום
בתחום 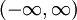 .
.
זו הרכבה של פונקציה רציפות במ"ש: 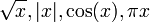 ולכן רציפה במ"ש בתחום.
ולכן רציפה במ"ש בתחום.
שאלה 7
חשב את הקירוב הלינארי של 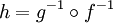 ב-
ב- 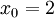 .
.
הקירוב הלינארי של 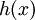 באזור הנקודה
באזור הנקודה 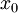 , הנו
, הנו 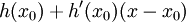
במקרה שלנו
![h'(2)=(g^{-1}\circ f^{-1})'(2)=\Big[\dfrac{d}{dx}g^{-1}\Big(f^{-1}(2)\Big)\Big]\cdot\Big[\dfrac{d}{dx}f^{-1}(2)\Big]=
\frac{1}{g'\Big(g^{-1}\big(f^{-1}(2)\big)\Big)}\cdot\dfrac1{f'\big(f^{-1}(2)\big)}](/images/math/e/3/5/e35770d449d3e811cdb6d8bc4f202cf0.png)
ולכן סה"כ 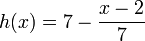
המבחן של דר' שמחה הורוביץ
שאלה 3
תהי 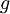 פונקציה רציפה במ"ש בקטע
פונקציה רציפה במ"ש בקטע 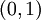 . נניח שקיים
. נניח שקיים 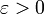 כך שמתקיים
כך שמתקיים 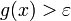 לכל
לכל 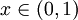 . הוכח שהפונקציה
. הוכח שהפונקציה  רציפה במ"ש בקטע
רציפה במ"ש בקטע 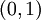 .
.
- הוכחה
לפי הנתון, לכל 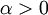 קיים
קיים 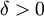 כך שאם
כך שאם 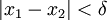 מתקיים
מתקיים 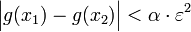 .
.
לכן, מתקיים 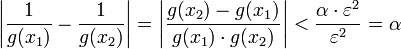
כפי שרצינו. 
שאלה 6
תהי  פונקציה בעלת חמש נגזרת רציפות על הממשיים. נניח ש-
פונקציה בעלת חמש נגזרת רציפות על הממשיים. נניח ש- 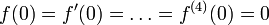 וגם
וגם 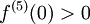 . עוד נניח שלכל
. עוד נניח שלכל 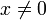 מתקיים
מתקיים 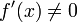 . הוכיחו שלכל
. הוכיחו שלכל 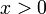 מתקיים
מתקיים 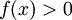 .
.
- הוכחה
מכיון שהפונקציה ו-4 נגזרותיה מתאפסות ב-0, פולינום טיילור מסדר 4 בסביבת הנקודה 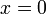 שווה זהותית ל-0. השארית היא מהצורה
שווה זהותית ל-0. השארית היא מהצורה 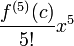 כאשר
כאשר 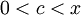 .
.
מכיון ש- 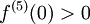 והנגזרת החמישית רציפה, אז קיימת סביבה של 0 בה
והנגזרת החמישית רציפה, אז קיימת סביבה של 0 בה 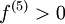 . לכן בסביבה ימנית של 0 מתקיים
. לכן בסביבה ימנית של 0 מתקיים 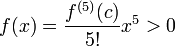 .
.
נותר להוכיח כי 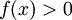 עבור
עבור 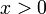 גם מחוץ לסביבה הימנית הזו. נניח בשלילה כי
גם מחוץ לסביבה הימנית הזו. נניח בשלילה כי 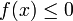 אזי לפי משפט ערך הביניים
אזי לפי משפט ערך הביניים 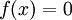 עבור
עבור 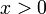 כלשהוא. אבל גם
כלשהוא. אבל גם 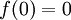 ולכן לפי משפט רול הנגזרת מתאפסת עבור נקודה גדולה מ-0, בסתירה.
ולכן לפי משפט רול הנגזרת מתאפסת עבור נקודה גדולה מ-0, בסתירה.