88-132 סמסטר א' תשעא/ פתרון מועד א'

המבחן של פרופ' זלצמן

שאלה 1

הוכח/הפרך: הסדרה a_n מתכנסת אם"ם לכל תת סדרה a_n_k יש תת סדרה מתכנסת

הפרכה

כל סדרה חסומה שאינה מתכנסת מהווה דוגמא נגדית, מכיוון שכל תת סדרה חסומה גם היא ולפי משפט בולצאנו ויירשטראס יש לה תת סדרה מתכנסת. (למשל 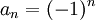$a_n=(-1)^n$)

שאלה 2

בדוק התכנסות של הטורים הבאים:

א

$\sum (-1)^n\frac{2^{n^3}}{(n!)^n}$

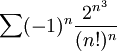
נבדוק התכנסות בהחלט, נפעיל מבחן קושי, לקבל:

$b_n=\sqrt[n]{|a_n|}=\frac{2^{n^2}}{n!}$

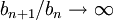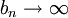קל לראות ש$b_{n+1}/b_n \rightarrow\infty$ ולכן $b_n\rightarrow\infty$. ולכן $|a_n|\rightarrow\infty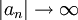$ ולכן הטור מתבדר לחלוטין

ב

$\sum (-1)^n\frac{sin(\frac{1}{n})}{(\log n)^2}$

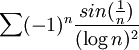
נבדוק התכנסות בהחלט. קל לראות ש

$\frac{\frac{sin(\frac{1}{n})}{(\log n)^2}}{\frac{1}{n(\log n)^2}}\rightarrow 1$

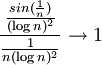
ולכן הטורים חברים. נוכיח שהשני מתכנס בעזרת מבחן העיבוי (מותר כי זו סדרה מונוטונית יורדת לאפס):

$\frac{2^n}{2^n(\log{2^n})^2}=\frac{1}{n^2(\log{2})^2}$

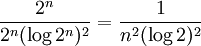
זה קבוע כפול טור שידוע כמתכנס, לכן סה"כ הטור מתכנס בהחלט.

ג

$\sum (-1)^n\frac{\pi^n}{\frac{(2n)!}{(n!)^2}}$

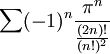
נבדוק התכנסות בהחלט, נפעיל את מבחן דלאמבר לקבל 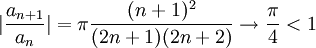$|\frac{a_{n+1}}{a_n}|=\pi\frac{(n+1)^2}{(2n+1)(2n+2)}\rightarrow \frac{\pi}{4}<1$

ולכן הטור מתכנס בהחלט.

שאלה 4

זהה וסווג את נקודות אי הרציפות

א

$e^{-\frac{1}{x^3}}$

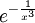
נקודת אי הרציפות היא אפס. הגבול משמאל הינו אינסוף ולכן זה מין שני.

ב

$\frac{sin(x^2)}{|sin(x^2)|}$

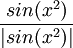
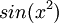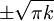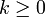כמו שלמדנו, הפונקציה הזו מקבלת אחד כאשר $sin(x^2)$ חיובי, ומינוס אחד כאשר הוא שלילי, באפס היא אינה מוגדרת ולכן זו נקודת אי רציפות. לכן סה"כ נקודות אי הרציפות הינן $\pm \sqrt{\pi k}$ כאשר $k\geq 0$. הן כולן מין ראשון מכיוון שמצד אחד של האפס הסינוס שלילי, ומהצד השני חיובי.