88-133 אינפי 2 תשעב סמסטר ב/הרצאות 3+4 (11+13/3/12)
הרצאות 3+4 (11+13/3/12)
נוסחה שהופיעה בשיעור:
את האינטגרל מהסוג 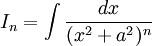 עבור
עבור 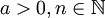 מחשבים בעזרת נוסחת הנסיגה הבאה:
מחשבים בעזרת נוסחת הנסיגה הבאה:
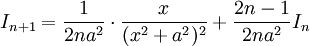 כך ש-
כך ש-
אינטגרציה של פונקציה רציונלית:
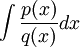 ,
, 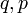 פולינומים.
פולינומים.
יש רק שני סוגים של שברים חלקיים:
(א) 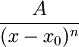 עבור
עבור 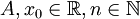
(ב) 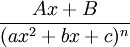 עבור
עבור 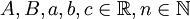 ולמכנה שאין לו שורשים ממשיים:
ולמכנה שאין לו שורשים ממשיים: 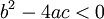
השיטה שלנו מתבססת על שני משפטים מאלגברה.
משפט 1: יהי 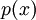 פולינום ממשי. אז ניתן לפרק את
פולינום ממשי. אז ניתן לפרק את 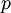 לקבוע כפול מספר איברים לינאריים
לקבוע כפול מספר איברים לינאריים 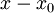 , ומספר איברים ריבועיים מהסוג
, ומספר איברים ריבועיים מהסוג 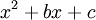 כך ש-
כך ש-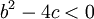 וזהו הפירוק המושלם של
וזהו הפירוק המושלם של 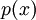 .
.
משפט 2: תהי 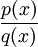 פונקציה רציונלית כך ש-
פונקציה רציונלית כך ש-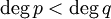 . אז אפשר לפרק את
. אז אפשר לפרק את 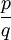 לסכום של שברים חלקיים.
לסכום של שברים חלקיים.
בפועל:
כדי לפרק את 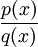 לסכום שברים חלקיים: תחילה מפרקים את
לסכום שברים חלקיים: תחילה מפרקים את 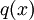 בצורה מושלמת עפ"י משפט 1, אז משווים את
בצורה מושלמת עפ"י משפט 1, אז משווים את 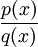 לסכום של שברים חלקיים כללי ביותר שעשוי להביא לידי המכנה
לסכום של שברים חלקיים כללי ביותר שעשוי להביא לידי המכנה 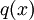 (זאת אומרת, המכנה הנשותף שלהם=
(זאת אומרת, המכנה הנשותף שלהם=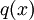 ).
).
רושמים את השברים החלקיים עם מקדמים בלתי ידועים ואז קובעים את המקדמים האלה. לבסוף מחשבים 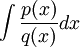 ע"י סכום אינטגרלים של השברים החלקיים שהם אינטגרלים קלים.
ע"י סכום אינטגרלים של השברים החלקיים שהם אינטגרלים קלים.
למידע נוסף ניתן לקבל בקישור הבא.
אינטגרציה של פונקציות רציונליות של 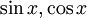 :
:
קיימת "הצבה אוניברסלית" שניתן בעזרתה להביא אינטגרל כזה לאינטגרל של פו' רציונלית רגילה שפתירה ע"י שברים חלקיים.
ההצבה היא: 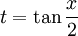
לכן 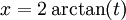 , לכן יוצא לפי גזירה ש-
, לכן יוצא לפי גזירה ש- 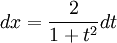 . נשתמש בזהות חשובה:
. נשתמש בזהות חשובה: 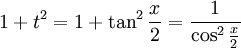 לכן:
לכן: 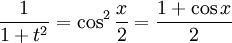 (לפי זהות לזוית כפולה)
(לפי זהות לזוית כפולה)
לאחר העברת אגפים יוצא ש- 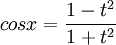 .
.
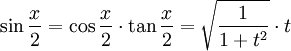
נשתמש כעת בזהות לזוית כפולה של 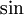 ונציב את הערכים שמצאנו כבר-
ונציב את הערכים שמצאנו כבר- 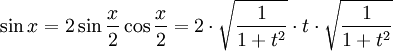
לכן יוצא ש- 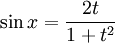
לבסוף נמצא את 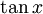 :
: 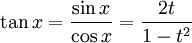
כללים נוספים:
אם נתון: 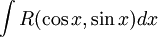 (במילים אחרות-פו' רציונלית
(במילים אחרות-פו' רציונלית 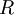 המורכבת מ
המורכבת מ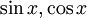 בלבד):
בלבד):
(א) אם 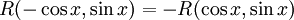 , תועיל ההצבה
, תועיל ההצבה 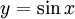 .
.
(ב) אם 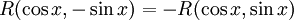 , תועיל ההצבה
, תועיל ההצבה 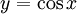 .
.
(ג) אם 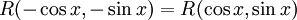 , תועיל ההצבה
, תועיל ההצבה 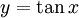 .
.
למקרה שיש טעות או שחסר חומר, תוכלו לפנות אליי דרך פייסבוק (שם המשתמש: Nimrod Sherer)