88-230 אינפי 3 סמסטר א תשעד הוכחות למשפטים למבחן
מתוך Math-Wiki
גרסה מ־19:14, 29 בינואר 2014 מאת Ofekgillon10 (שיחה | תרומות)
תוכן עניינים
משפט קנטור על רציפות במ"ש
המשפט
תהי 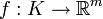 כך ש-
כך ש- 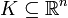 קבוצה קומפקטית ו-
קבוצה קומפקטית ו- רציפה ב-
רציפה ב- 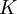 , אזי f רציפה במ"ש ב-K. (הרצאה 6)
, אזי f רציפה במ"ש ב-K. (הרצאה 6)
הוכחה
נניח בשלילה ש-f לא רבמ"ש ב-K. אז מתקיים ש-
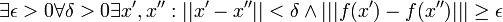 .
.
זה מתקיים לכל דלתא, אז נגדיר סדרה של דלתות באופן הבא: 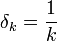 , ולכל
, ולכל 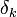 נסמן את
נסמן את 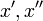 בהתאם:
בהתאם: 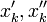 .
.
לכן לכל k מתקיים: 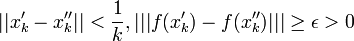
כיוון שכל הנקודות 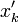 ב-K, שהיא קבוצה קומפקטית, מתקיימת למת בולצאנו ווירשטראס. כלומר קיימת תת סדרה
ב-K, שהיא קבוצה קומפקטית, מתקיימת למת בולצאנו ווירשטראס. כלומר קיימת תת סדרה 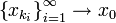 שמתכנסת לנקודה
שמתכנסת לנקודה 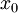 שגם היא ב-K (כיוון ש-K סגורה).
שגם היא ב-K (כיוון ש-K סגורה).
נשים לב ש- 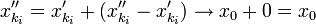 . מתוך הנתון ש- f רציפה ב-
. מתוך הנתון ש- f רציפה ב- 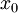 נקבל ש-
נקבל ש- 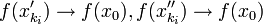 אך אם כך,
אך אם כך, 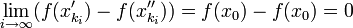 בסתירה לכך שקיים אפסילון כך ש-
בסתירה לכך שקיים אפסילון כך ש- 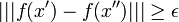 . משל
. משל
היחס בין הדיפרנציאל לנגזרות החלקיות
הערה: יש 2 משפטים שאני לא בטוח לאיזה אחד מהם הוא מתכוון, וצריך לשאול אותו. (שניהם בהרצאה 7)
משפט 1
תהי 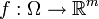 כך ש-
כך ש- 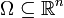 ותהי
ותהי 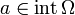 כך ש- f דיפ' ב-a. אזי לכל
כך ש- f דיפ' ב-a. אזי לכל 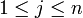 קיימת נגזרת חלקית
קיימת נגזרת חלקית 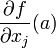 והיא שווה ל-
והיא שווה ל- 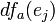
משפט 2
תהי 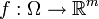 כך ש-
כך ש- 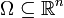 ותהי
ותהי 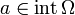 כך ש- f דיפ' ב-a, אזי מתקיים:
כך ש- f דיפ' ב-a, אזי מתקיים: