88-236 אינפי 4 תשעב סמסטר ב/המחשות
המחשות מתרגול 1:
בתרגול הראשון הגדרנו בקצרה ושרטטנו שדות סקלריים ווקטוריים. הנה ציורים יותר יפים שלהם (הוקטורים לא באורך המדויק, אבל מקבלים תמונה כללית):
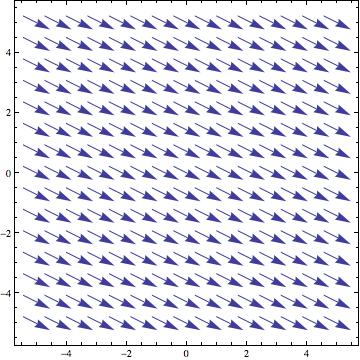
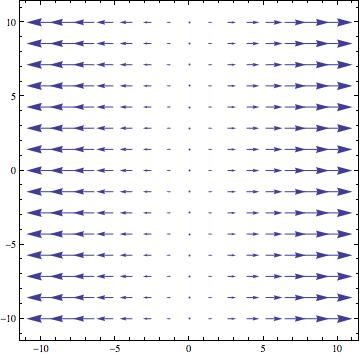
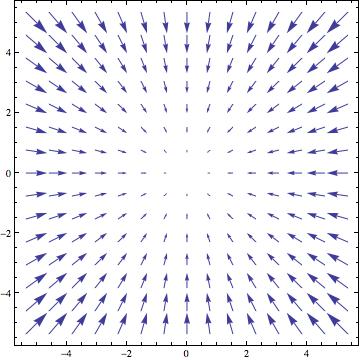
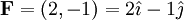 (שדה וקטורי קבוע)
(שדה וקטורי קבוע)
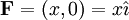
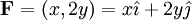
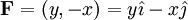
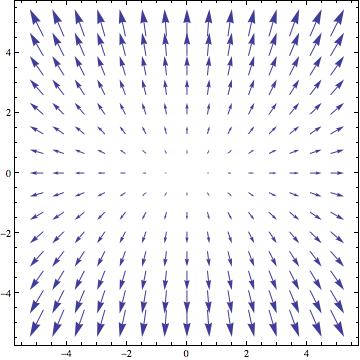
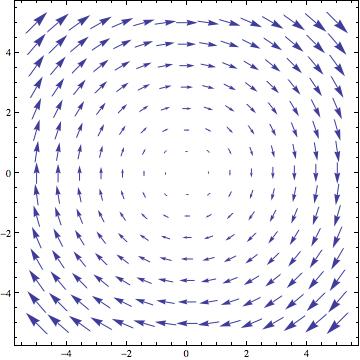
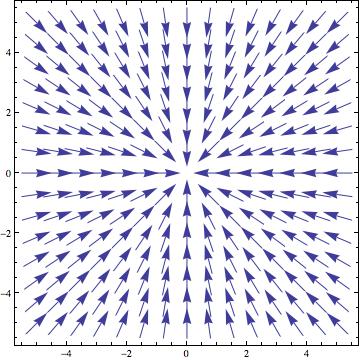
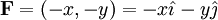 (בכל נקודה (x,y) השדה מצביע בכוון ההפוך (x,-y-). בעקרון כל החצים צריכים להגיע לראשית אבל אז הציור יוצא פחות ברור...)
(בכל נקודה (x,y) השדה מצביע בכוון ההפוך (x,-y-). בעקרון כל החצים צריכים להגיע לראשית אבל אז הציור יוצא פחות ברור...)
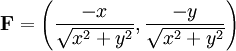
נשים לב שזהו הנרמול של השדה הוקטורי הקודם, שכן:
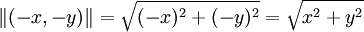
כלומר, הוקטורים מצביעים באותו כיוון כמו מקודם, אבל אורכם יהיה זהה.
הערה: כפי שנאמר בתרגול, השדה הזה לא מוגדר בראשית בגלל שהמכנה מתאפס שם.
נדבר כעת על השדה הסקלרי (פונקציה סקלרית) 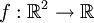 המוגדר על ידי
המוגדר על ידי 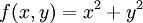
את הגרף של  נוכל לצייר ב-
נוכל לצייר ב-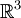 (מרחב
(מרחב 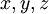 ) כאשר
) כאשר 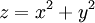
את הגרדיאנט של  אפשר לחשב בקלות:
אפשר לחשב בקלות:
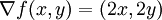
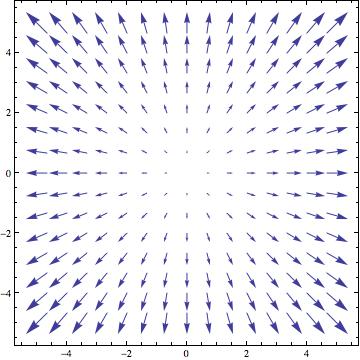
זהו שדה וקטורי, שנראה כך:
כפי שנאמר בכיתה, השדה הגרדיאנטי מצביע תמיד בכוון העלייה התלולה ביותר בפונקציה (במקרה זה הוא מצביע הרחק מהראשית).
עקומות הרמה במקרה זה הן העקומות שבהן 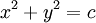 כאשר
כאשר 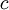 קבוע. אם
קבוע. אם 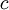 שלילי זוהי קבוצה ריקה. אם
שלילי זוהי קבוצה ריקה. אם 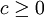 מדובר במעגל בעל רדיוס
מדובר במעגל בעל רדיוס 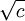 שמרכזו ב-
שמרכזו ב-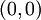 . הנה אנימציה שבה חותכים את המשטח
. הנה אנימציה שבה חותכים את המשטח 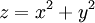 עם המישור הקבוע
עם המישור הקבוע 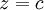 עבור ערכים שונים של
עבור ערכים שונים של 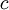 (אולי לא כל כך בקרוב...)
(אולי לא כל כך בקרוב...)