88-341 תשעג סמסטר א/תרגילים/תרגיל 5
שאלה 1
תזכורת: מידה 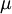 על מרחב מדיד
על מרחב מדיד 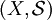 נקראת שלמה אם לכל קבוצה מדידה
נקראת שלמה אם לכל קבוצה מדידה 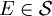 , עבורה
, עבורה 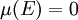 , מתקיים שכל תת-קבוצה שלה
, מתקיים שכל תת-קבוצה שלה 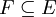 היא מדידה (כלומר נמצאת ב-
היא מדידה (כלומר נמצאת ב-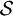 ).
).
יהי 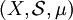 מרחב מידה חיובית ושלמה ותהי
מרחב מידה חיובית ושלמה ותהי 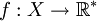 פונקציה מדידה. תהי
פונקציה מדידה. תהי 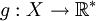 פונקציה השווה ל-
פונקציה השווה ל- כמעט בכל מקום, ז"א
כמעט בכל מקום, ז"א 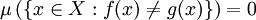 . הוכיחו כי
. הוכיחו כי 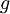 אף היא מדידה.
אף היא מדידה.
שאלה 2
בתרגיל הקודם הוכחנו שלכל 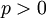 מתקיים
מתקיים 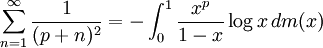 . לא קשה לראות שהנוסחה נכונה גם עבור
. לא קשה לראות שהנוסחה נכונה גם עבור 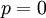 , ובמקרה זה מקבלים
, ובמקרה זה מקבלים 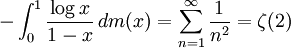 , כאשר
, כאשר 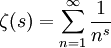 היא פונקצית זטא של רימן.
היא פונקצית זטא של רימן.
הוכיחו את ההכללה הבאה של תוצאה זו: לכל 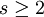 טבעי
טבעי 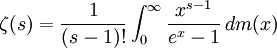 .
.
הדרכה:
א. הוכיחו כי לכל 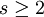 וטבעי מתקיים
וטבעי מתקיים 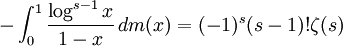 (ההוכחה דומה לתרגיל הקודם).
(ההוכחה דומה לתרגיל הקודם).
ב. בצעו החלפת משתנים מתאימה, כלומר כזו שתעביר את תחום האינטגרציה מהקטע 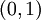 אל הקרן
אל הקרן 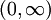 (אולי עדיף לפצל לשתי החלפות משתנים).
(אולי עדיף לפצל לשתי החלפות משתנים).
ג. ברכות! מצאתם ייצוג אינטגרלי של פונקציית זטא.
שאלה 3
יהיו 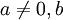 מספרים ממשיים, ותהי
מספרים ממשיים, ותהי 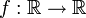 מדידה לבג ואינטגרבילית. הוכיחו כי מתקיים
מדידה לבג ואינטגרבילית. הוכיחו כי מתקיים 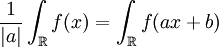 .
.
הדרכה:
א. הוכיחו זאת תחילה לפונקציות אינדיקטור. לשם כך בדקו מהי הפונקציה 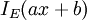 כאשר
כאשר 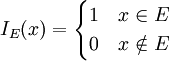
ב. הוכיחו כי הטענה נכונה גם לפונקציות פשוטות.
ג. הוכיחו זאת לפונקציות חיוביות כלשהן בעזרת משפט ההתכנסות המונוטונית של לבג.
ד. כדי להראות זאת לפונקציה כללית, אפשר להראות שאם 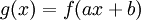 , אזי
, אזי 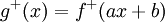 ו-
ו-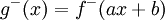 . כאשר
. כאשר 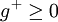 ו-
ו-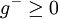 הן החלק החיובי והחלק השלילי בהתאמה של הפונקציה
הן החלק החיובי והחלק השלילי בהתאמה של הפונקציה 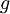 .
.
בהצלחה!