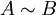הבדלים בין גרסאות בדף "פתרון ליניארית 2, אונ' בר אילן, תשעא, מועד א', שאלה 4"
Noamlifshitz (שיחה | תרומות) |
|||
| (5 גרסאות ביניים של 2 משתמשים אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
'''השאלה:''' | '''השאלה:''' | ||
| − | נניח שלמטריצות <math>A,B\in \mathbb{C}^{3 \times 3}</math> יש אותו פולינום אופייני, וכן אותו פולינום מינימלי, הוכח שהמטריצות A | + | נניח שלמטריצות <math>A,B\in \mathbb{C}^{3 \times 3}</math> יש אותו פולינום אופייני, וכן אותו פולינום מינימלי, הוכח שהמטריצות <math>A</math> ו <math>B</math> דומות. |
'''פתרון:''' | '''פתרון:''' | ||
| − | |||
| − | ''' | + | '''הגדרה:''' |
| − | + | ||
| − | + | האינדקס של ערך עצמי <math>\lambda</math> הוא <math>max\{k : (x-\lambda)^{k}\vert m_{A}(x)\}</math> | |
| − | + | ||
| − | <math> | + | |
| − | <math> | + | כאשר יש ע"ע יחיד הפולינום האופייני הוא <math>(x-\lambda)^{3}</math> כמו שהראנו קודם |
| − | <math> | + | בגלל שהפולינום המינימלי מחלק את הפולינום האופייני האינדקס של <math>\lambda\in\{1,2,3\}</math> |
| − | + | '''נניח שהאינדקס 1''' | |
| + | נקבל שהבלוק ג'ורדן הכי גדול בצורת ג'ורדן הוא מסדר 1 | ||
| + | כלומר קיבלנו מטריצה סקלרית <math>\lambda I</math> ולכן היא יחידה | ||
| − | + | '''נניח שהאינדקס 2''' | |
| − | + | נקבל שבצורת ג'ורדן הבלוק הכי גדול <math>J_{m}(\lambda)</math> הוא עבור m=2 ולכן נשאר לנו מקום רק לבלוק מסדר אחד כלומר צורת ג'ורדן מורכבת מ <math>J_{2}(\lambda)</math>,<math>J_{1}(\lambda)</math> | |
| + | '''נניח שהאינדקס 3''' | ||
| − | + | נקבל שיש רק בלוק אחד מסדר 3 | |
| − | + | בסופו של דבר הראנו שהפולינום האופייני והמינימלי מגדירים באופן יחיד את צורת הג'ורדן ולכן נניח יש ל-A ול-B אתו פוינום אופיינו ומינימלי נקבל: | |
| − | <math>\ | + | <math>B\sim J_{B}=J_{A}\sim A</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ומטרנזיטיביות של דמיון מטריצות<math>A \sim B</math> | |
| + | נניח שיש 2 שורשים שונים <math>\lambda_{1},\lambda_{2}</math> כלומר 2 ערכים עצמיים שונים נניח בלי הגבלת הכלליות : | ||
| − | + | <math>f_{A}\left(x\right)=\left(x-\lambda_{2}\right)^{2}\left(x-\lambda_{1}\right)</math> | |
| − | + | נבדוק כל אחד מהאפשרויות עבור האינדקס של<math>\lambda_{2}</math> | |
| − | + | '''נניח שהוא 1''' | |
| − | <math> | + | נקבל שכל בלוק הוא מסדר 1 (כי האינדקס קטן מהריבוי האלגברי והריבוי האלגברי של<math>\lambda_{1}</math> הוא 1) |
| + | ולכן יש צורת ג'ורדן יחידה אלכסונית | ||
| − | + | '''נניח שהוא 2''' | |
| − | + | נקבל שקיים בלוק מסדר 2 וזה חייב להיות <math>\lambda_{2}</math> ולכן עוד פעם צורת ג'ורדן מוגדרת באופן יחיד ע"י הפולינים: האופייני והמינימלי ולכן מאותו נימוק כמו קודם: | |
| + | <math>B\sim J_{B}=J_{A}\sim A</math> | ||
| − | + | ומטרנזיטיביות של דמיון מטריצות <math>A \sim B</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <math> | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
גרסה אחרונה מ־23:09, 8 בינואר 2012
השאלה:
נניח שלמטריצות 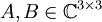 יש אותו פולינום אופייני, וכן אותו פולינום מינימלי, הוכח שהמטריצות
יש אותו פולינום אופייני, וכן אותו פולינום מינימלי, הוכח שהמטריצות  ו
ו  דומות.
דומות.
פתרון:
הגדרה:
האינדקס של ערך עצמי 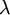 הוא
הוא 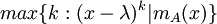
כאשר יש ע"ע יחיד הפולינום האופייני הוא 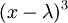 כמו שהראנו קודם
כמו שהראנו קודם
בגלל שהפולינום המינימלי מחלק את הפולינום האופייני האינדקס של 
נניח שהאינדקס 1
נקבל שהבלוק ג'ורדן הכי גדול בצורת ג'ורדן הוא מסדר 1
כלומר קיבלנו מטריצה סקלרית 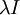 ולכן היא יחידה
ולכן היא יחידה
נניח שהאינדקס 2
נקבל שבצורת ג'ורדן הבלוק הכי גדול 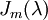 הוא עבור m=2 ולכן נשאר לנו מקום רק לבלוק מסדר אחד כלומר צורת ג'ורדן מורכבת מ
הוא עבור m=2 ולכן נשאר לנו מקום רק לבלוק מסדר אחד כלומר צורת ג'ורדן מורכבת מ 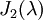 ,
,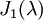
נניח שהאינדקס 3
נקבל שיש רק בלוק אחד מסדר 3
בסופו של דבר הראנו שהפולינום האופייני והמינימלי מגדירים באופן יחיד את צורת הג'ורדן ולכן נניח יש ל-A ול-B אתו פוינום אופיינו ומינימלי נקבל:
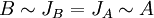
ומטרנזיטיביות של דמיון מטריצות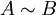
נניח שיש 2 שורשים שונים 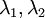 כלומר 2 ערכים עצמיים שונים נניח בלי הגבלת הכלליות :
כלומר 2 ערכים עצמיים שונים נניח בלי הגבלת הכלליות :
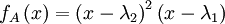
נבדוק כל אחד מהאפשרויות עבור האינדקס של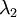
נניח שהוא 1
נקבל שכל בלוק הוא מסדר 1 (כי האינדקס קטן מהריבוי האלגברי והריבוי האלגברי של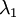 הוא 1)
ולכן יש צורת ג'ורדן יחידה אלכסונית
הוא 1)
ולכן יש צורת ג'ורדן יחידה אלכסונית
נניח שהוא 2
נקבל שקיים בלוק מסדר 2 וזה חייב להיות 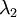 ולכן עוד פעם צורת ג'ורדן מוגדרת באופן יחיד ע"י הפולינים: האופייני והמינימלי ולכן מאותו נימוק כמו קודם:
ולכן עוד פעם צורת ג'ורדן מוגדרת באופן יחיד ע"י הפולינים: האופייני והמינימלי ולכן מאותו נימוק כמו קודם:
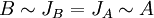
ומטרנזיטיביות של דמיון מטריצות