הבדלים בין גרסאות בדף "88-230 אינפי 3 סמסטר א תשעד הוכחות למשפטים למבחן"
Ofekgillon10 (שיחה | תרומות) |
Ofekgillon10 (שיחה | תרומות) (←משפט) |
||
| (14 גרסאות ביניים של אותו משתמש אינן מוצגות) | |||
| שורה 1: | שורה 1: | ||
| + | [[88-230 אינפי 3 סמסטר א תשעד]] | ||
| + | |||
==משפט קנטור על רציפות במ"ש== | ==משפט קנטור על רציפות במ"ש== | ||
===המשפט=== | ===המשפט=== | ||
| שורה 17: | שורה 19: | ||
==היחס בין הדיפרנציאל לנגזרות החלקיות== | ==היחס בין הדיפרנציאל לנגזרות החלקיות== | ||
| − | + | צריך לדעת את 3 הדברים שבחלק זה (המשפטים בהרצאה 7 והדוגמה לקוחה מהתרגול) | |
===משפט 1=== | ===משפט 1=== | ||
| שורה 59: | שורה 61: | ||
ובאופן דומה לנגזרת החלקית לפי y | ובאופן דומה לנגזרת החלקית לפי y | ||
| + | |||
| + | ==מהגדרה של דיפרנציאל מסדר r לנוסחה עם נגזרות חלקיות== | ||
| + | ===הגדרה=== | ||
| + | תהי <math>f \in C^r(U)</math> כך ש- U קבוצה פתוחה ומוכלת ב- <math>\mathbb{R}^n</math>. | ||
| + | |||
| + | יהי <math>h \in \mathbb{R}^n</math>. נגדיר <math>\varphi(t)=f(a+th)</math>, אז מתקיים ש- <math>\varphi</math> גזירה r פעמים ב-0. | ||
| + | |||
| + | לכן ניתן להגדיר: <math>d^rf_a(h):=\varphi^{(r)}(0)</math> | ||
| + | |||
| + | ===משפט=== | ||
| + | <math>d^rf_a(h)=\sum_{|\alpha| =r} \frac{r!}{\alpha!}D^{\alpha}f(a)\cdot h^\alpha</math> | ||
| + | |||
| + | (הרצאה 12) | ||
| + | |||
| + | כך ש- | ||
| + | |||
| + | <math>\alpha=(\alpha_1,...,\alpha_n)</math> מולטי אינדקס | ||
| + | |||
| + | <math>|\alpha|=\sum_{i=1}^n |\alpha_i|</math> | ||
| + | |||
| + | <math>\alpha! = \alpha_1!\cdot ... \cdot \alpha_n!</math> | ||
| + | |||
| + | <math>h^\alpha = h_1^{\alpha_1}\cdot ... \cdot h_n^{\alpha_n}</math> | ||
| + | |||
| + | <math>D^\alpha f = \frac{\partial^{|\alpha|} f} {\partial x_1^{\alpha_1} ... \partial x_n^{\alpha_n} }</math> | ||
| + | |||
| + | ===הוכחה=== | ||
| + | [[מדיה:ProofTheorem3AdvancedCalc2014.docx | להורדת ההוכחה]] | ||
==תנאי מספיק לדיפרנציאביליות לפי רציפות נגזרות חלקיות== | ==תנאי מספיק לדיפרנציאביליות לפי רציפות נגזרות חלקיות== | ||
| + | ===המשפט=== | ||
| + | תהי <math>f:\Omega \to \mathbb{R}^m</math> ותהי נקודה <math>a\in \operatorname{int} \Omega</math> | ||
| + | |||
| + | נניח ש- | ||
| + | |||
| + | 1. עבור דלתא מספר קטן קיימות <math>\forall_{1\leq i \leq n}\forall x \in B(a,\delta):\frac{\partial f}{\partial x_i} (x)</math> | ||
| + | |||
| + | 2. כל הנגזרות החלקיות רציפות בכדור הזה. | ||
| + | |||
| + | אזי f דיפ' ב-a. (הרצאה 9) | ||
| + | |||
| + | ==תנאי מספיק לקיצון מקומי עפ"י הדיפרנציאל השני== | ||
| + | ===המשפט=== | ||
| + | תהי <math>f:U\to \mathbb{R}</math> כך ש-U קבוצה פתוחה שמוכלת ב- <math>\mathbb{R}^n</math> ו- <math>f\in C^2(U)</math>. | ||
| + | |||
| + | תהי <math>a \in U</math> נק' קריטית של f (כלומר <math>\nabla f(a)=0</math>) אזי: | ||
| + | |||
| + | 1. אם <math>d^2f_a>0</math> אז a מינימום מקומית ממש | ||
| + | |||
| + | 2. אם <math>d^2f_a<0</math> אז a מקסימום מקומית ממש | ||
| + | |||
| + | 3. אם <math>d^2f_a</math> לא שומרת סימן אז a לא קיצון. | ||
| + | |||
| + | (הרצאה 15) | ||
| + | |||
| + | ==משפט פונקציה סתומה - משוואה אחת== | ||
| + | |||
| + | ===משפט=== | ||
| + | תהי <math>W \subseteq \mathbb{R}^n \times \mathbb{R}</math> קבוצה פתוחה ותהי <math>F:W\to \mathbb R</math> כך ש- <math>F \in C^r (W)</math> | ||
| + | |||
| + | נתונה הנקודה <math>(a,b)</math> כך ש- | ||
| + | |||
| + | 1. <math>F(a,b)=0</math> | ||
| + | |||
| + | 2. <math>\frac{\partial f}{\partial y} (a,b)\neq 0</math> (כאשר y זה המשתנה ה- n+1) | ||
| + | |||
| + | אזי קיימות סביבות <math>a \in U , b \in V</math> כך ש- <math>\forall_{x \in U} \exists!_{y \in V} : F(x,y)=0</math>. | ||
| + | |||
| + | כלומר קיימת פונקציה <math>\varphi:U\to V</math> כך ש- <math>F(x,\varphi(x))=0</math>. בנוסף <math>\varphi \in C^r(U)</math> | ||
| + | |||
| + | (הרצאה 16) | ||
| + | |||
| + | ==משפט פונקציה סתומה - מקרה כללי== | ||
| + | ===משפט=== | ||
| + | |||
| + | ==תנאי הכרחי לקיצון עם אילוצים== | ||
| + | ===משפט=== | ||
| + | |||
| + | ==קריטריון רימן לאינטגרביליות== | ||
| + | ===משפט=== | ||
| + | תהי <math>f:P\to \mathbb{R}</math> כך ש- <math>\exists C \forall x \in P: ||f(x)||\leq C</math>, אזי <math>f \in \mathcal{R}(P)</math> (אינטגרבילית לפי רימן) אם ורק אם | ||
| + | |||
| + | <math>\forall \epsilon>0 \exists \mathcal{P} : 0\leq \bar{S}(f,\mathcal{P})-\underline{S}(f,\mathcal{P}) < \epsilon</math> | ||
| + | |||
| + | כלומר לכל אפסילון קיימת חלוקה כך שההפרש בין הסכומים העליוניים לתחתוניים קטן מאפסילון. | ||
| + | |||
| + | (הרצאה 21) | ||
| + | |||
| + | ===הוכחה=== | ||
| + | '''משמאל לימין:''' | ||
| + | |||
| + | יהי <math>\epsilon>0</math> אזי קיימת חלוקה <math>\mathcal{P}</math> כך ש- <math> 0\leq \bar{S}(f,\mathcal{P})-\underline{S}(f,\mathcal{P})< \epsilon</math>. כלומר <math> 0\leq \bar{S}(f,\mathcal{P})<\underline{S}(f,\mathcal{P})+ \epsilon</math> ומכאן ש- <math>\bar{I}(f)=\operatorname{inf}_{\mathcal Q} \bar{S}(f, \mathcal Q) < \underline{S}(f,\mathcal{P})+ \epsilon</math> | ||
| + | |||
| + | אז <math>\bar{I}(f)-\epsilon<\underline{S}(f,\mathcal{P})\leq \operatorname{sup}_{\mathcal Q} \underline{S}(f,\mathcal{Q}) = \underline{I}(f)</math> ולכן <math>\overline{I}(f)-\underline{I}(f)<\epsilon</math> לכל אפסילון גדול מ-0. לכן <math>\overline{I}(f)-\underline{I}(f)=0</math> ואז <math>\overline{I}(f)=\underline{I}(f)</math>. אז <math>f \in \mathcal{R} (P)</math> | ||
| + | |||
| + | '''מימין לשמאל:''' | ||
| + | |||
| + | נניח <math>f \in \mathcal{R} (P)</math> אז <math>\overline{I}(f)=\operatorname{inf}_{\mathcal Q} \bar{S}(f, \mathcal Q)=\operatorname{sup}_{\mathcal Q} \underline{S}(f,\mathcal{Q}) =\underline{I}(f)=I(f)</math> | ||
| + | |||
| + | יהי אפסילון גדול מ-0 | ||
| + | |||
| + | אז | ||
| + | |||
| + | <math>\exists \mathcal Q : I(f)-\frac\epsilon2 < \underline{S}(f,\mathcal{Q})\leq I(f)</math> | ||
| + | |||
| + | <math>\exists \mathcal P : I(f)+\frac\epsilon2 > \bar S(f,\mathcal{P})\geq I(f)</math> | ||
| + | |||
| + | לכן קיימות חלוקות <math>\mathcal {P , Q}</math> כך ש- | ||
| + | |||
| + | <math>I(f)-\frac\epsilon2 < \underline{S}(f,\mathcal{Q}) \leq \bar S(f,\mathcal{P}) < I(f)+\frac\epsilon2 </math> | ||
| + | |||
| + | נגדיר <math>\mathcal T := \mathcal P \cap \mathcal Q</math> (לא מצאתי דרך לבטא את החיתוך עם העיגול מעל. זה הכוונה פה) | ||
| + | |||
| + | <math>I(f)-\frac\epsilon2 < \underline{S}(f,\mathcal{Q})\leq\underline{S}(f,\mathcal{T})\leq \bar S(f,\mathcal{T})\leq \bar S(f,\mathcal{P}) < I(f)+\frac\epsilon2</math> | ||
| + | |||
| + | <math>\bar S(f,\mathcal{T}) -\underline{S}(f,\mathcal{T}) < I(f)+\frac\epsilon2-(I(f)-\frac\epsilon2)=\epsilon </math> | ||
| + | |||
| + | משל | ||
גרסה אחרונה מ־18:36, 1 בפברואר 2014
תוכן עניינים
- 1 משפט קנטור על רציפות במ"ש
- 2 היחס בין הדיפרנציאל לנגזרות החלקיות
- 3 מהגדרה של דיפרנציאל מסדר r לנוסחה עם נגזרות חלקיות
- 4 תנאי מספיק לדיפרנציאביליות לפי רציפות נגזרות חלקיות
- 5 תנאי מספיק לקיצון מקומי עפ"י הדיפרנציאל השני
- 6 משפט פונקציה סתומה - משוואה אחת
- 7 משפט פונקציה סתומה - מקרה כללי
- 8 תנאי הכרחי לקיצון עם אילוצים
- 9 קריטריון רימן לאינטגרביליות
משפט קנטור על רציפות במ"ש
המשפט
תהי 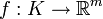 כך ש-
כך ש- 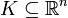 קבוצה קומפקטית ו-
קבוצה קומפקטית ו-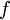 רציפה ב-
רציפה ב- 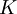 , אזי f רציפה במ"ש ב-K. (הרצאה 6)
, אזי f רציפה במ"ש ב-K. (הרצאה 6)
הוכחה
נניח בשלילה ש-f לא רבמ"ש ב-K. אז מתקיים ש-
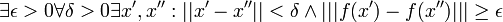 .
.
זה מתקיים לכל דלתא, אז נגדיר סדרה של דלתות באופן הבא: 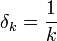 , ולכל
, ולכל 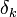 נסמן את
נסמן את 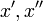 בהתאם:
בהתאם: 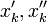 .
.
לכן לכל k מתקיים: 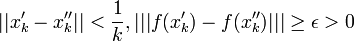
כיוון שכל הנקודות 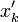 ב-K, שהיא קבוצה קומפקטית, מתקיימת למת בולצאנו ווירשטראס. כלומר קיימת תת סדרה
ב-K, שהיא קבוצה קומפקטית, מתקיימת למת בולצאנו ווירשטראס. כלומר קיימת תת סדרה 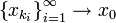 שמתכנסת לנקודה
שמתכנסת לנקודה 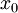 שגם היא ב-K (כיוון ש-K סגורה).
שגם היא ב-K (כיוון ש-K סגורה).
נשים לב ש- 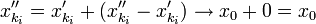 . מתוך הנתון ש- f רציפה ב-
. מתוך הנתון ש- f רציפה ב- 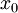 נקבל ש-
נקבל ש- 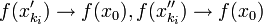 אך אם כך,
אך אם כך, 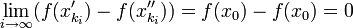 בסתירה לכך שקיים אפסילון כך ש-
בסתירה לכך שקיים אפסילון כך ש- 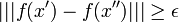 . משל
. משל
היחס בין הדיפרנציאל לנגזרות החלקיות
צריך לדעת את 3 הדברים שבחלק זה (המשפטים בהרצאה 7 והדוגמה לקוחה מהתרגול)
משפט 1
תהי 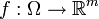 כך ש-
כך ש- 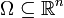 ותהי
ותהי 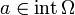 כך ש- f דיפ' ב-a. אזי לכל
כך ש- f דיפ' ב-a. אזי לכל 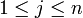 קיימת נגזרת חלקית
קיימת נגזרת חלקית 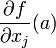 והיא שווה ל-
והיא שווה ל- 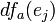
(הערה: משפט זה הוא מקרה פרטי למשפט שהוכחנו בהמשך באופן דומה. המשפט אומר ש- 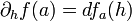 כך ש-
כך ש- 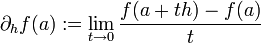 זוהי הנגזרת הכיוונית לפי וקטור h.)
זוהי הנגזרת הכיוונית לפי וקטור h.)
הוכחה 1
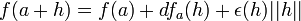 כך ש-
כך ש- 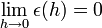 .
.
לכן,
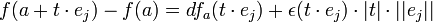
כיוון ש- 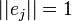 והדיפרנציאל הוא אופרטור לינארי, מקבלים ש-
והדיפרנציאל הוא אופרטור לינארי, מקבלים ש-
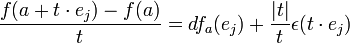
נשים לב שהגורם האחרון שואף ל-0 כש- t שואף ל-0, ולכן נקבל:
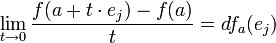 אך אגף שמאל, עפ"י הגדרה, זה
אך אגף שמאל, עפ"י הגדרה, זה 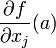 וקיבלנו את מה שרצינו.
וקיבלנו את מה שרצינו.
משפט 2
תהי 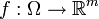 כך ש-
כך ש- 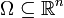 ותהי
ותהי 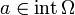 כך ש- f דיפ' ב-a, אזי מתקיים:
כך ש- f דיפ' ב-a, אזי מתקיים:
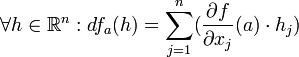
הוכחה 2
יהי 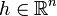 אז
אז 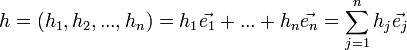 . מתוך העובדה שהדיפרנציאל הוא אופרטור לינארי וממשפט 1,
. מתוך העובדה שהדיפרנציאל הוא אופרטור לינארי וממשפט 1,
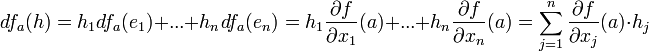
דוגמה בה כל הנגזרות החלקיות קיימות אבל הפונקציה לא דיפרנציאבילית
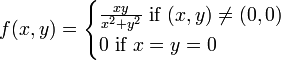
הפונקציה אפילו לא רציפה ב-0! (ניקח מסלולים y=kx ונקבל גבולות שונים)
אך הנגזרות החלקיות קיימות:
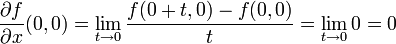
ובאופן דומה לנגזרת החלקית לפי y
מהגדרה של דיפרנציאל מסדר r לנוסחה עם נגזרות חלקיות
הגדרה
תהי 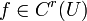 כך ש- U קבוצה פתוחה ומוכלת ב-
כך ש- U קבוצה פתוחה ומוכלת ב- 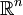 .
.
יהי 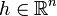 . נגדיר
. נגדיר 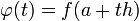 , אז מתקיים ש-
, אז מתקיים ש- 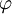 גזירה r פעמים ב-0.
גזירה r פעמים ב-0.
לכן ניתן להגדיר: 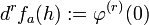
משפט
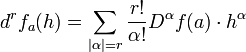
(הרצאה 12)
כך ש-
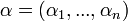 מולטי אינדקס
מולטי אינדקס
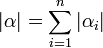
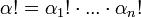
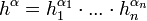
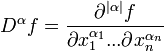
הוכחה
תנאי מספיק לדיפרנציאביליות לפי רציפות נגזרות חלקיות
המשפט
תהי 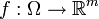 ותהי נקודה
ותהי נקודה 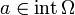
נניח ש-
1. עבור דלתא מספר קטן קיימות 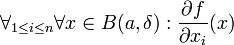
2. כל הנגזרות החלקיות רציפות בכדור הזה.
אזי f דיפ' ב-a. (הרצאה 9)
תנאי מספיק לקיצון מקומי עפ"י הדיפרנציאל השני
המשפט
תהי 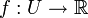 כך ש-U קבוצה פתוחה שמוכלת ב-
כך ש-U קבוצה פתוחה שמוכלת ב- 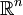 ו-
ו- 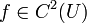 .
.
תהי 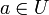 נק' קריטית של f (כלומר
נק' קריטית של f (כלומר 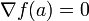 ) אזי:
) אזי:
1. אם 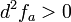 אז a מינימום מקומית ממש
אז a מינימום מקומית ממש
2. אם 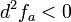 אז a מקסימום מקומית ממש
אז a מקסימום מקומית ממש
3. אם 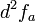 לא שומרת סימן אז a לא קיצון.
לא שומרת סימן אז a לא קיצון.
(הרצאה 15)
משפט פונקציה סתומה - משוואה אחת
משפט
תהי 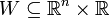 קבוצה פתוחה ותהי
קבוצה פתוחה ותהי 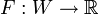 כך ש-
כך ש- 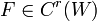
נתונה הנקודה 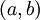 כך ש-
כך ש-
1. 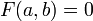
2. 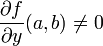 (כאשר y זה המשתנה ה- n+1)
(כאשר y זה המשתנה ה- n+1)
אזי קיימות סביבות 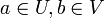 כך ש-
כך ש- 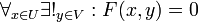 .
.
כלומר קיימת פונקציה 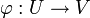 כך ש-
כך ש- 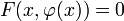 . בנוסף
. בנוסף 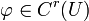
(הרצאה 16)
משפט פונקציה סתומה - מקרה כללי
משפט
תנאי הכרחי לקיצון עם אילוצים
משפט
קריטריון רימן לאינטגרביליות
משפט
תהי 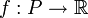 כך ש-
כך ש- 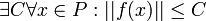 , אזי
, אזי 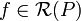 (אינטגרבילית לפי רימן) אם ורק אם
(אינטגרבילית לפי רימן) אם ורק אם
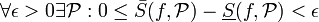
כלומר לכל אפסילון קיימת חלוקה כך שההפרש בין הסכומים העליוניים לתחתוניים קטן מאפסילון.
(הרצאה 21)
הוכחה
משמאל לימין:
יהי 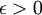 אזי קיימת חלוקה
אזי קיימת חלוקה 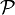 כך ש-
כך ש- 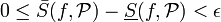 . כלומר
. כלומר 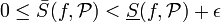 ומכאן ש-
ומכאן ש- 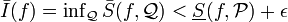
אז 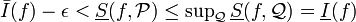 ולכן
ולכן 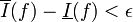 לכל אפסילון גדול מ-0. לכן
לכל אפסילון גדול מ-0. לכן 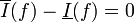 ואז
ואז 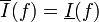 . אז
. אז 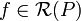
מימין לשמאל:
נניח 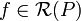 אז
אז 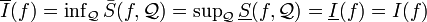
יהי אפסילון גדול מ-0
אז
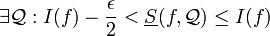
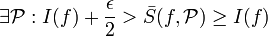
לכן קיימות חלוקות 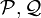 כך ש-
כך ש-
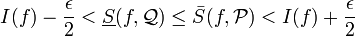
נגדיר 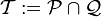 (לא מצאתי דרך לבטא את החיתוך עם העיגול מעל. זה הכוונה פה)
(לא מצאתי דרך לבטא את החיתוך עם העיגול מעל. זה הכוונה פה)
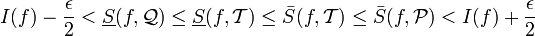
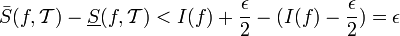
משל