גרסה מ־08:38, 26 באוגוסט 2021

הטבעיים [math]\displaystyle{ \mathbb{N}=\{1,2,3,...\} }[/math]
השלמים [math]\displaystyle{ \mathbb{Z}=\{0,-1,1,-2,2,...\} }[/math]
הרציונאליים [math]\displaystyle{ \mathbb{Q}=\left\{\frac{p}{n}|p\in\mathbb{Z},n\in\mathbb{N}\right\} }[/math]
הממשיים [math]\displaystyle{ \mathbb{R} }[/math], כל השברים העשרוניים כולל האינסופיים

העשרה: בנייה של שדה הממשיים באמצעות חתכי דדקינד

לא קיים [math]\displaystyle{ x\in\mathbb{Q} }[/math] כך ש [math]\displaystyle{ x^2=2 }[/math].
במילים פשוטות, [math]\displaystyle{ \sqrt{2} }[/math] אינו רציונאלי (בהמשך נוכיח שיש מספר ממשי כזה).

חזקות ולוגריתמים

לכל מספר ממשי [math]\displaystyle{ x\in\mathbb{R} }[/math] ולכל מספר טבעי [math]\displaystyle{ n\in\mathbb{N} }[/math] נגדיר [math]\displaystyle{ x^n=x\cdots x }[/math] כפל n פעמים
לכל מספר ממשי אי שלילי [math]\displaystyle{ 0\leq x\in\mathbb{R} }[/math] ולכל מספר טבעי [math]\displaystyle{ n\in\mathbb{N} }[/math] נגדיר [math]\displaystyle{ x^{\frac{1}{n}}=\sqrt[n]{x} }[/math] כלומר המספר האי שלילי שבחזקת n שווה לx.
לכל מספר ממשי אי שלילי [math]\displaystyle{ 0\leq x\in\mathbb{R} }[/math] ולכל זוג מספרים טבעיים [math]\displaystyle{ n,k\in\mathbb{N} }[/math] נגדיר [math]\displaystyle{ x^{\frac{n}{k}}=\sqrt[k]{x^n} }[/math]
לכל מספר ממשי [math]\displaystyle{ x\in\mathbb{R} }[/math] נגדיר [math]\displaystyle{ x^0=1 }[/math]

מה לגבי חזקות ממשיות אי רציונליות?
נגדיר אותן באמצעות גבול של חזקות רציונאליות

לכל מספר ממשי [math]\displaystyle{ x\in\mathbb{R} }[/math] ולכל חזקה ממשית שלילית [math]\displaystyle{ -a\lt 0 }[/math] נגדיר [math]\displaystyle{ x^{-a}=\frac{1}{x^a} }[/math]

לכל [math]\displaystyle{ 0\lt a\neq 1 }[/math] נגדיר את [math]\displaystyle{ log_a(x) }[/math] להיות המספר שa בחזקתו שווה לx.
חוקי לוגים:
- [math]\displaystyle{ log_a(x)+log_a(y)=log_a(xy) }[/math]
- [math]\displaystyle{ log_a(x)-log_a(y)=log_a\left(\frac{x}{y}\right) }[/math]
- [math]\displaystyle{ log_a(x^y)=y log_a(x) }[/math]
- [math]\displaystyle{ \log_a(x)=\frac{log_b(x)}{log_b(a)} }[/math]
- [math]\displaystyle{ log_a(x)=y }[/math] אם ורק אם [math]\displaystyle{ x=a^y }[/math]

חסמים

תהי [math]\displaystyle{ A\subseteq \mathbb{R} }[/math] אזי:
- [math]\displaystyle{ M\in\mathbb{A} }[/math] נקרא המקסימום של A או האיבר הגדול ביותר של A אם לכל [math]\displaystyle{ a\in A }[/math] מתקיים כי [math]\displaystyle{ a\leq M }[/math]
- [math]\displaystyle{ M\in\mathbb{R} }[/math] נקרא חסם מלעיל של A אם לכל [math]\displaystyle{ a\in A }[/math] מתקיים כי [math]\displaystyle{ a\leq M }[/math]
- [math]\displaystyle{ m\in\mathbb{A} }[/math] נקרא המינימום של A או האיבר הקטן ביותר של A אם לכל [math]\displaystyle{ a\in A }[/math] מתקיים כי [math]\displaystyle{ a\geq m }[/math]
- [math]\displaystyle{ m\in\mathbb{R} }[/math] נקרא חסם מלרע של A אם לכל [math]\displaystyle{ a\in A }[/math] מתקיים כי [math]\displaystyle{ a\geq m }[/math]

כמו כן:
- אם יש איבר קטן ביותר בקבוצת חסמי המלעיל של A הוא נקרא החסם העליון של A, או הסופרמום של A ומסומן [math]\displaystyle{ \sup(A) }[/math]
- אם יש איבר גדול ביותר בקבוצת חסמי המלרע של A הוא נקרא החסם התחתון של A, או האינפימום של A ומסומן [math]\displaystyle{ \inf(A) }[/math]

בשדה הממשיים לכל קבוצה לא ריקה וחסומה מלעיל יש חסם עליון, ולכל קבוצה לא ריקה וחסומה מלרע יש חסם תחתון.
בשדה הרציונאליים זה לא נכון; לקבוצה [math]\displaystyle{ A=\{x\in\mathbb{Q}|x^2\lt 2\} }[/math] אין מספר רציונאלי קטן ביותר מבין חסמי המלעיל שלה.

תהי [math]\displaystyle{ A\subseteq \mathbb{R} }[/math] ויהי [math]\displaystyle{ M\in\mathbb{R} }[/math] אזי:
- M הוא החסם העליון של A אם ורק אם M הוא חסם מלעיל של A ולכל מספר [math]\displaystyle{ M-\varepsilon\lt M }[/math] קיים מספר [math]\displaystyle{ a\in A }[/math] כך ש [math]\displaystyle{ a\gt M-\varepsilon }[/math]
- m הוא החסם התחתון של A אם ורק אם m הוא חסם מלרע של A ולכל מספר [math]\displaystyle{ m\lt m+\varepsilon }[/math] קיים מספר [math]\displaystyle{ a\in A }[/math] כך ש [math]\displaystyle{ a\lt m+\varepsilon }[/math]

דוגמא: תהיינה [math]\displaystyle{ \emptyset\neq A,B\subseteq\mathbb{R} }[/math] חסומות מלעיל כך שA אינה מכילה חסמי מלעיל של B, אזי [math]\displaystyle{ \sup(A)\leq\sup(B) }[/math]

שיטות הוכחה בסיסיות

שיטות הוכחה בסיסיות

הוכחת טענות מכומתות - טענות 'לכל' וטענות 'קיים'

פרק 2 - סדרות

הגדרת הגבול

הגדרת הגבול של סדרה:
תהי סדרה ממשית [math]\displaystyle{ a_n }[/math] ויהי מספר ממשי [math]\displaystyle{ L\in\mathbb{R} }[/math].
[math]\displaystyle{ L }[/math] הינו גבול הסדרה [math]\displaystyle{ a_n }[/math] (מסומן [math]\displaystyle{ \lim a_n=L }[/math] או [math]\displaystyle{ a_n\to L }[/math]) אם:
- לכל סביבה של הגבול, קיים מקום בסדרה שאחריו כל איברי הסדרה נמצאים בסביבה הנתונה, כלומר:
- לכל מרחק [math]\displaystyle{ \varepsilon\gt 0 }[/math] קיים מקום [math]\displaystyle{ K\in\mathbb{N} }[/math] כך שאחריו לכל [math]\displaystyle{ n\gt K }[/math] מתקיים כי [math]\displaystyle{ |a_n-L|\lt \varepsilon }[/math]

נגדיר ש[math]\displaystyle{ a_n\to\infty }[/math] אם1

לכל [math]\displaystyle{ M\gt 0 }[/math] קיים [math]\displaystyle{ K\in\mathbb{N} }[/math] כך שלכל [math]\displaystyle{ n\gt K }[/math] מתקיים כי [math]\displaystyle{ a_n\gt M }[/math]

נגדיר ש[math]\displaystyle{ a_n\to -\infty }[/math] אם [math]\displaystyle{ -a_n\to\infty }[/math]

טענה: תהי [math]\displaystyle{ a_n\to \infty }[/math] אזי [math]\displaystyle{ \frac{1}{a_n}\to 0 }[/math]
טענה: תהי [math]\displaystyle{ 0\neq a_n\to 0 }[/math] אזי [math]\displaystyle{ \frac{1}{|a_n|}\to\infty }[/math]

אם [math]\displaystyle{ a_n\to L_1 }[/math] וכן [math]\displaystyle{ a_n\to L_2 }[/math] אזי [math]\displaystyle{ L_1=L_2 }[/math]

סדרה המתכנסת לגבול סופי חסומה.

[math]\displaystyle{ a_n\to L \iff a_{n+1}\to L }[/math]
בפרט, כל שינוי, תוספת או החסרה של מספר סופי של איברים לא משפיע על גבול הסדרה.

תהי סדרה[math]\displaystyle{ a_n }[/math] המתכנסת לגבול סופי והמקיימת לכל [math]\displaystyle{ n }[/math] כי [math]\displaystyle{ a\lt a_n }[/math] אזי [math]\displaystyle{ \lim a_n\geq a }[/math]

שאיפה לאפס

תהי סדרה [math]\displaystyle{ a_n }[/math] ויהי [math]\displaystyle{ L\in\mathbb{R} }[/math] אזי [math]\displaystyle{ a_n\to L }[/math] אם ורק אם [math]\displaystyle{ |a_n-L|\to 0 }[/math]
- בפרט [math]\displaystyle{ a_n\to 0 }[/math] אם ורק אם [math]\displaystyle{ |a_n|\to 0 }[/math]

תהי [math]\displaystyle{ a_n\to 0 }[/math] ותהי [math]\displaystyle{ b_n }[/math] חסומה, אזי [math]\displaystyle{ a_nb_n\to 0 }[/math]

תהיינה [math]\displaystyle{ a_n,b_n\to 0 }[/math] אזי גם [math]\displaystyle{ a_n+b_n\to 0 }[/math]

משפטי סנדביץ'

משפט הסנדביץ' -
- תהיינה סדרות המקיימות לכל n כי [math]\displaystyle{ a_n\leq b_n \leq c_n }[/math]
- כמו כן, יהי [math]\displaystyle{ L\in\mathbb{R} }[/math] כך ש [math]\displaystyle{ a_n,c_n\to L }[/math]
- אזי [math]\displaystyle{ b_n\to L }[/math]
חצי סנדביץ'-
- תהיינה סדרות המקיימות לכל n כי [math]\displaystyle{ a_n\leq b_n }[/math]
- כמו כן נתון כי [math]\displaystyle{ a_n\to\infty }[/math]
- אזי [math]\displaystyle{ b_n\to \infty }[/math]
חצי סנדביץ' על הרצפה -
- תהיינה סדרות המקיימות לכל n כי [math]\displaystyle{ |a_n|\leq b_n }[/math]
- כמו כן נתון כי [math]\displaystyle{ b_n\to 0 }[/math]
- אזי [math]\displaystyle{ a_n\to 0 }[/math]

מבוא לחשבון גבולות (אריתמטיקה של גבולות)

תהיינה [math]\displaystyle{ b_n\to L_b\in \mathbb{R} }[/math], [math]\displaystyle{ a_n\to L_a\in \mathbb{R} }[/math] אזי
- [math]\displaystyle{ a_n+b_n\to L_a+L_b }[/math]
- [math]\displaystyle{ a_n\cdot b_n \to L_a\cdot L_b }[/math]
- אם [math]\displaystyle{ L_b\neq 0 }[/math] אזי [math]\displaystyle{ \frac{a_n}{b_n}\to\frac{L_a}{L_b} }[/math]

אינדוקציה

משפט האינדוקציה המתמטית
תהי סדרת טענות כך שמתקיימים שני התנאים הבאים:
- הטענה הראשונה נכונה.
- לכל [math]\displaystyle{ n\in \mathbb{N} }[/math] אם הטענה הn מתקיימת אז גם הטענה הn+1 מתקיימת.
אזי כל הטענות בסדרה נכונות

אי שיוויון ברנולי: יהי [math]\displaystyle{ -1\lt x\in\mathbb{R} }[/math] אזי לכל [math]\displaystyle{ n\in\mathbb{N} }[/math] מתקיים כי [math]\displaystyle{ (1+x)^n\geq 1+nx }[/math]

חזקת אינסוף

תהי [math]\displaystyle{ 0\lt a_n\to a }[/math] אזי:
- אם [math]\displaystyle{ a\gt 1 }[/math] מתקיים כי [math]\displaystyle{ (a_n)^n \to \infty }[/math]
- אם [math]\displaystyle{ a\lt 1 }[/math] מתקיים כי [math]\displaystyle{ (a_n)^n\to 0 }[/math]
שימו לב כי ייתכן ו[math]\displaystyle{ 1\lt a_n\to 1 }[/math], כלומר איברי הסדרה גדולים מ1 אך גבולה הוא 1 ואז המשפט אינו תקף.

כלל המנה

כלל המנה (הוכחה בסיכום הבא על אי-שוויון הממוצעים).
- תהי סדרה [math]\displaystyle{ a_n }[/math] המקיימת כי גבול המנה הוא [math]\displaystyle{ \left|\frac{a_{n+1}}{a_n}\right|\to L }[/math] אזי:
  - אם [math]\displaystyle{ 1\lt L\leq\infty }[/math] מתקיים כי [math]\displaystyle{ |a_n|\to\infty }[/math]
  - אם [math]\displaystyle{ 0\leq L\lt 1 }[/math] מתקיים כי [math]\displaystyle{ a_n\to 0 }[/math]
  - מתקיים כי [math]\displaystyle{ \sqrt[n]{|a_n|}\to L }[/math]

דוגמאות:
- [math]\displaystyle{ \frac{n}{2^n}\to 0 }[/math]
- [math]\displaystyle{ \sqrt[n]{n}\to 1 }[/math]
- עבור [math]\displaystyle{ a\gt 0 }[/math] מתקיים [math]\displaystyle{ \sqrt[n]{a}\to 1 }[/math]
- [math]\displaystyle{ \sqrt[n]{n!}\to \infty }[/math]

חזקות של גבולות

יהי [math]\displaystyle{ 0\lt a\in\mathbb{R} }[/math] ותהי [math]\displaystyle{ b_n\to 0 }[/math] אזי [math]\displaystyle{ a^{b_n}\to 1 }[/math]
- רעיון הוכחה: אם [math]\displaystyle{ a\geq 1 }[/math] אזי [math]\displaystyle{ a^{-\frac{1}{m}}\leq a^{b_n}\leq a^{\frac{1}{m}} }[/math] והרי [math]\displaystyle{ \sqrt[m]{a}\to 1 }[/math] לפי כלל המנה

יהי [math]\displaystyle{ 0\lt a\in\mathbb{R} }[/math] ותהי [math]\displaystyle{ b_n\to L\in \mathbb{R} }[/math] אזי [math]\displaystyle{ a^{b_n}\to a^L }[/math]
- רעיון הוכחה: [math]\displaystyle{ a^{b_n} = a^{b_n-L}\cdot a^L\to 1\cdot a^L }[/math]

תהי [math]\displaystyle{ a_n\to 1 }[/math] ותהי [math]\displaystyle{ b_n\to L\in\mathbb{R} }[/math] אזי [math]\displaystyle{ a_n^{b_n}\to 1 }[/math]
- רעיון הוכחה:[math]\displaystyle{ a_n^{[L]-1}\leq a_n^{b_n}\leq a_n^{[L]+1} }[/math] לפי חשבון גבולות (כפל) שני הצדדים שואפים ל1. (אם [math]\displaystyle{ a_n\lt 1 }[/math] אי השיוויון הפוך).

תהי [math]\displaystyle{ a_n\to a\gt 0 }[/math] ותהי [math]\displaystyle{ b_n\to L\in\mathbb{R} }[/math] אזי [math]\displaystyle{ a_n^{b_n}\to a^L }[/math]
- רעיון הוכחה: [math]\displaystyle{ a_n^{b_n}=\left(\frac{a_n}{a}\right)^{b_n} \cdot a^{b_n} \to 1\cdot a^L }[/math]

תהי [math]\displaystyle{ 0\leq a_n\to 0 }[/math] ותהי [math]\displaystyle{ b_n\to L\gt 0 }[/math] אזי [math]\displaystyle{ a_n^{b_n}\to 0 }[/math]
- רעיון הוכחה: החל משלב מסויים [math]\displaystyle{ 0\leq a_n^{b_n}\leq \frac{1}{m^{\frac{L}{2}}} }[/math]

סדרות מונוטוניות והמספר e

כל סדרה מונוטונית הינה חסומה מתכנסת לגבול סופי, או שאינה חסומה ושואפת לגבול אינסופי.

דוגמא: נביט בסדרה [math]\displaystyle{ a_1\gt 0,\ a_{n+1}=a_n^2+a_n }[/math]
- כיוון ש [math]\displaystyle{ a_{n+1}-a_n=a_n^2\geq 0 }[/math] מדובר בסדרה מונוטונית עולה.
- אם הסדרה חסומה:
  - קיים לה גבול סופי [math]\displaystyle{ a_n\to L }[/math]
  - נחשב את גבול שני צידי המשוואה [math]\displaystyle{ a_{n+1}=a_n^2+a_n }[/math]
  - לכן [math]\displaystyle{ L=L^2+L }[/math] ולכן [math]\displaystyle{ L=0 }[/math]
  - אבל הסדרה עולה וחסומה מלמטה ע"י האיבר הראשון ולכן [math]\displaystyle{ L\geq a_1 }[/math]
  - כלומר [math]\displaystyle{ L=0\lt a_1\leq L }[/math] בסתירה.
- מכאן הסדרה אינה חסומה, וכיוון שהיא עולה [math]\displaystyle{ a_n\to\infty }[/math]

המספר e (הוכחות בעזרת אי-שוויון הממוצעים).

[math]\displaystyle{ 2\lt e\lt 4 }[/math].

תתי סדרות וגבולות חלקיים

הגדרת גבול חלקי

לכל סדרת מקומות [math]\displaystyle{ k_n\in\mathbb{N} }[/math] המקיימת לכל [math]\displaystyle{ n }[/math] כי [math]\displaystyle{ k_n\lt k_{n+1} }[/math] נגדיר כי [math]\displaystyle{ a_{k_n} }[/math] הינה תת סדרה של הסדרה [math]\displaystyle{ a_n }[/math]
שימו לב כי מקומות תת הסדרה הם באותו הסדר כמו בסדרה המקורית, ואסור לחזור על איבר פעמיים.

לדוגמא:
- נביט בסדרה [math]\displaystyle{ a_n=(-1)^n }[/math]
- אזי [math]\displaystyle{ a_{2n}=(-1)^{2n}=1 }[/math] היא תת הסדרה של האיברים במקומות הזוגיים [math]\displaystyle{ k_n=2n }[/math]

נגדיר ש[math]\displaystyle{ L }[/math] הוא גבול חלקי של הסדרה [math]\displaystyle{ a_n }[/math] אם קיימת תת סדרה [math]\displaystyle{ a_{k_n} }[/math] כך ש [math]\displaystyle{ a_{k_n}\to L }[/math]

טענה - יהי [math]\displaystyle{ L }[/math] סופי או אינסופי, אזי:
- [math]\displaystyle{ a_n\to L }[/math] אם ורק אם לכל תת סדרה [math]\displaystyle{ a_{k_n} }[/math] מתקיים כי [math]\displaystyle{ a_{k_n}\to L }[/math]

משפט בולצאנו-ויירשטראס

לכל סדרה יש תת סדרה מונוטונית.

משפט בולצאנו-ויירשטראס - לכל סדרה חסומה יש תת סדרה מתכנסת.

גבול עליון וגבול תחתון

תהי סדרה [math]\displaystyle{ a_n }[/math]
נגדיר את הגבול העליון שלה (limsup):
- אם [math]\displaystyle{ a_n }[/math] אינה חסומה מלעיל אזי [math]\displaystyle{ \overline{\lim}a_n=\infty }[/math]
- אם [math]\displaystyle{ a_n }[/math] חסומה מלעיל ויש לה גבול חלקי סופי כלשהו, נגדיר את [math]\displaystyle{ \overline{\lim}a_n }[/math] להיות החסם העליון של קבוצת הגבולות החלקיים של הסדרה
- אחרת, נגדיר [math]\displaystyle{ \overline{\lim}a_n=-\infty }[/math]
נגדיר את הגבול התחתון שלה (liminf):
- אם [math]\displaystyle{ a_n }[/math] אינה חסומה מלרע אזי [math]\displaystyle{ \underline{\lim}a_n=-\infty }[/math]
- אם [math]\displaystyle{ a_n }[/math] חסומה מלרע ויש לה גבול חלקי סופי כלשהו, נגדיר את [math]\displaystyle{ \underline{\lim}a_n }[/math] להיות החסם התחתון של קבוצת הגבולות החלקיים של הסדרה
- אחרת, נגדיר [math]\displaystyle{ \underline{\lim}a_n=\infty }[/math]

לכל גבול חלקי L של הסדרה מתקיים כי:
[math]\displaystyle{ \underline{\lim}a_n\leq L\leq \overline{\lim}a_n }[/math]

הגבול העליון והגבול התחתון הם גבולות חלקיים (כלומר יש תת סדרה ששואפת לגבול העליון, ויש תת סדרה ששואפת לגבול התחתון).

לכל [math]\displaystyle{ -\infty\leq L\leq \infty }[/math] מתקיים כי [math]\displaystyle{ a_n \to L }[/math] אם ורק אם [math]\displaystyle{ \underline{\lim}a_n=\overline{\lim}a_n=L }[/math]

תתי סדרות המכסות סדרה

אם ניתן לחלק סדרה למספר סופי של תתי סדרות המכסות את כולה, וכולן שואפות לאותו הגבול - אזי הסדרה כולה שואפת לגבול זה.
ייתכן שניתן לחלק סדרה לאינסוף תתי סדרות שכולם שואפות לאותו הגבול, אך הסדרה לא תשאף לגבול זה.

כלל הe

תהי [math]\displaystyle{ 0\neq a_n\to 0 }[/math] אזי [math]\displaystyle{ (1+a_n)^{\frac{1}{a_n}}\to e }[/math]

אם [math]\displaystyle{ a_n\to 1 }[/math] אזי [math]\displaystyle{ a_n^{b_n}\to e^{\lim b_n\cdot(a_n-1)} }[/math]
- [math]\displaystyle{ a_n^{b_n}=\left[\left(1+(a_n-1)\right)^{\frac{1}{a_n-1}}\right]^{ b_n\cdot (a_n-1)} }[/math].
- [math]\displaystyle{ \left(1+(a_n-1)\right)^{\frac{1}{a_n-1}}\to e }[/math] בין אם [math]\displaystyle{ a_n-1 }[/math] שלילי או חיובי, לפי הטענות לעיל.
- שימו לב שאם [math]\displaystyle{ a_n=1 }[/math], אז ממילא מקבלים 1 בנוסחא הסופית, ואז לא צריך לחלק ב[math]\displaystyle{ a_n-1 }[/math] ששווה אפס.

דוגמא:
- [math]\displaystyle{ \lim\left(\frac{n+1}{n-2}\right)^n=e^{\lim n\cdot\left(\frac{n+1}{n-2}-1\right)}=e^{\lim\frac{3n}{n-2}}=e^3 }[/math]

חשבון גבולות (אריתמטיקה של גבולות)

אריתמטיקה מורחבת (הכתיב הוא מקוצר ואינו מדוייק):
- חסומה כפול אפיסה = אפיסה
- חסומה חלקי אינסוף = אפיסה
- [math]\displaystyle{ \infty+\infty=\infty }[/math]
- [math]\displaystyle{ \infty\cdot\infty=\infty }[/math]
- [math]\displaystyle{ \infty^\infty=\infty }[/math]
- [math]\displaystyle{ \frac{1}{0}\neq\infty }[/math]
- [math]\displaystyle{ \frac{1}{0^+}=\infty }[/math]
- [math]\displaystyle{ 0^\infty = 0 }[/math]
- אינסוף כפול סדרה השואפת למספר חיובי = אינסוף.
- יש גבול סופי + אין גבול סופי = אין גבול סופי.
- אינסוף ועוד חסומה שווה אינסוף.
- אינסוף בחזקת מספר חיובי זה אינסוף
- סדרה השואפת לגבול גדול מאחד, בחזקת אינסוף זה אינסוף.
- סדרה השואפת לגבול בין מינוס אחד לאחד לא כולל, בחזקת אינסוף, זה אפס.

המקרים הבעייתיים

המקרים הבעייתיים בהם צריך להפעיל מניפולציות אלגבריות או משפטים על מנת לחשב את הגבול:
- [math]\displaystyle{ \frac{0}{0},\frac{\infty}{\infty},0\cdot\infty,\infty-\infty,0^0,\infty^0,1^\infty }[/math]

קריטריון קושי לסדרות

דוגמא: הסדרה [math]\displaystyle{ a_n=\sqrt{n} }[/math] מקיימת כי [math]\displaystyle{ a_{n+1}-a_n\to 0 }[/math] אך היא אינה מתכנסת למספר סופי אלא שואפת לאינסוף.

הגדרה: סדרה [math]\displaystyle{ a_n }[/math] מקיימת את קריטריון קושי (ונקראת סדרת קושי) אם:
לכל מרחק [math]\displaystyle{ \varepsilon\gt 0 }[/math] קיים מקום [math]\displaystyle{ K\in\mathbb{N} }[/math] כך שאחריו לכל זוג מקומות [math]\displaystyle{ m\gt n\gt K }[/math] מתקיים כי [math]\displaystyle{ |a_m-a_n|\lt \varepsilon }[/math] (המרחק בין האיברים במקומות הללו קטן מאפסילון).

משפט: בממשיים, סדרה מתכנסת לגבול סופי אם ורק אם היא סדרת קושי.

תרגיל: תהי סדרה המקיימת לכל n כי [math]\displaystyle{ |a_{n+1}-a_n|\lt \frac{1}{2^n} }[/math] אזי היא מתכנסת למספר סופי.

פרק 3 - טורים

מבוא והגדרה

תהי סדרה [math]\displaystyle{ a_n }[/math], נגדיר את סדרת הסכומים החלקיים (סס"ח בקיצור) של [math]\displaystyle{ a_n }[/math] ע"י
- [math]\displaystyle{ S_1=a_1 }[/math]
- ולכל [math]\displaystyle{ n\in\mathbb{N} }[/math] מתקיים [math]\displaystyle{ S_{n+1}=S_n+a_{n+1} }[/math]
במילים אחרות, [math]\displaystyle{ S_n = \sum_{k=1}^n a_k }[/math]

הגדרת הטור [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math]
- אומרים כי [math]\displaystyle{ \sum_{k=1}^\infty a_k =L }[/math] אם [math]\displaystyle{ \lim S_n = L }[/math]
אם לסס"ח יש גבול סופי אומרים כי הטור מתכנס, ואילו אם אין לה גבול סופי אומרים כי הטור מתבדר.
שימו לב כי בעצם:
- [math]\displaystyle{ \sum_{k=1}^\infty a_k = \lim_{n\to\infty}\sum_{k=1}^n a_k }[/math]

אם הטור [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתכנס, אזי [math]\displaystyle{ a_n\to 0 }[/math]
הוכחה:
- [math]\displaystyle{ S_n,S_{n+1}\to L }[/math]
- לכן [math]\displaystyle{ a_{n+1}=S_{n+1}-S_n\to L-L=0 }[/math]

[math]\displaystyle{ \sum_{k=1}^\infty a_k = a_1 + \sum_{k=2}^\infty a_k }[/math]
מסקנה: שינוי מספר סופי של איברי הטור לא משפיע על התכנסות, אבל כן משפיע על סכום הטור.

חשבון טורים

אם הטור [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתכנס, ו[math]\displaystyle{ c\in\mathbb{R} }[/math] קבוע אזי
- [math]\displaystyle{ \sum_{k=1}^\infty c\cdot a_k = c\cdot \sum_{k=1}^\infty a_k }[/math]

אם הטורים [math]\displaystyle{ \sum_{k=1}^\infty a_k,\ \sum_{k=1}^\infty b_k }[/math] מתכנסים אזי
- [math]\displaystyle{ \sum_{k=1}^\infty (a_k+b_k) = \sum_{k=1}^\infty a_k + \sum_{k=1}^\infty b_k }[/math]

הטור ההנדסי

הטור [math]\displaystyle{ \sum_{k=0}^\infty x^k }[/math] מתכנס אם ורק אם [math]\displaystyle{ |x|\lt 1 }[/math] וכאשר הוא מתכנס מתקיים כי:
- [math]\displaystyle{ \sum_{k=0}^\infty x^k = \frac{1}{1-x} }[/math] וכמו כן [math]\displaystyle{ \sum_{k=1}^\infty x^k = \frac{x}{1-x} }[/math]

טור מקל סלפי (טלסקופי)

חישוב [math]\displaystyle{ \sum_{k=2}^\infty \frac{1}{k^2 -k} }[/math] על ידי הסס"ח הטלסקופי

חישוב [math]\displaystyle{ \sum_{k=1}^\infty \ln\left(\frac{k}{k+1}\right) }[/math] על ידי הסס"ח הטלסקופי

העשרה על סוגי סכימה

התכנסות בהחלט

משפט: אם טור הערכים המוחלטים [math]\displaystyle{ \sum_{k=1}^\infty |a_k| }[/math] מתכנס, אזי גם הטור המקורי [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתכנס.

הגדרה:
- הטור [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] נקרא מתכנס בהחלט אם [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתכנס וגם [math]\displaystyle{ \sum_{k=1}^\infty |a_k| }[/math] מתכנס
- הטור [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] נקרא מתכנס בתנאי אם [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתכנס אך [math]\displaystyle{ \sum_{k=1}^\infty |a_k| }[/math] מתבדר
- הטור [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] נקרא מתבדר אם [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתבדר וגם [math]\displaystyle{ \sum_{k=1}^\infty |a_k| }[/math] מתבדר

משפט: (הכללת אי שיוויון המשולש) יהי טור מתכנס בהחלט, אזי:
[math]\displaystyle{ \left|\sum_{k=0}^\infty a_k\right|\leq \sum_{k=0}^\infty |a_k| }[/math]

הוכחה:
לפי אי שיוויון המשולש, לכל n סופי מתקיים כי
[math]\displaystyle{ \left|\sum_{k=0}^n a_k\right|\leq \sum_{k=0}^n |a_k| }[/math]
ולכן גם הגבול של הסדרה השמאלית קטן או שווה לגבול של הסדרה הימנית, וזו התוצאה שרצינו.

מבחני התכנסות לטורים חיוביים

הקדמה והטור ההרמוני

הגדרה: טור [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] נקרא טור חיובי אם לכל n מתקיים כי [math]\displaystyle{ a_n\geq 0 }[/math].
סדרת הסכומים החלקיים של טור חיובי היא מונוטונית עולה, לכן הטור מתכנס אם ורק אם היא חסומה.

לסס"ח של הטור ההרמוני [math]\displaystyle{ \sum_{k=1}^\infty \frac{1}{k} }[/math] יש תת סדרה ששואפת לאינסוף, ולכן הטור מתבדר:
- [math]\displaystyle{ \frac{1}{n+1}+...+\frac{1}{2n}\geq \frac{1}{2n}+...+\frac{1}{2n}=\frac{n}{2n}=\frac{1}{2} }[/math]
- [math]\displaystyle{ S_1 =1\geq \frac{1}{2} }[/math]
- [math]\displaystyle{ S_2 =1+\frac{1}{2}\geq 2\cdot \frac{1}{2} }[/math]
- [math]\displaystyle{ S_4 =1+\frac{1}{2} + \frac{1}{3} + \frac{1}{4}\geq 3\cdot \frac{1}{2} }[/math]
- ...
- באופן כללי [math]\displaystyle{ S_{2^{n-1}}\geq n\cdot \frac{1}{2}\to\infty }[/math]

מבחני ההשוואה

מבחן ההשוואה הראשון-
תהיינה סדרות כך ש [math]\displaystyle{ 0\leq a_n\leq b_n }[/math] לכל n. אזי:
- אם הטור הגדול יותר [math]\displaystyle{ \sum_{k=1}^\infty b_k }[/math] מתכנס בוודאי הטור הקטן יותר [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתכנס.
- נובע מכך לוגית שאם הטור הקטן מתבדר, הטור הגדול מתבדר.

דוגמא:
- [math]\displaystyle{ \frac{1}{n^2} \leq \frac{1}{n^2-n} }[/math]
- ראינו שהטור החיובי [math]\displaystyle{ \sum_{k=2}^\infty \frac{1}{k^2-k} }[/math] מתכנס ולכן לפי מבחן ההשוואה הראשון גם הטור החיובי [math]\displaystyle{ \sum_{k=1}^\infty\frac{1}{k^2} }[/math] מתכנס

מבחן ההשוואה הגבולי-
תהיינה סדרות [math]\displaystyle{ 0\leq a_n,b_n }[/math] כך ש [math]\displaystyle{ \frac{a_n}{b_n}\to c }[/math] אזי:
- אם [math]\displaystyle{ c=\infty }[/math] אזי [math]\displaystyle{ a_n\gt b_n }[/math] החל משלב מסויים, ולכן אם [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתכנס גם [math]\displaystyle{ \sum_{k=1}^\infty b_k }[/math] מתכנס
- אם [math]\displaystyle{ c=0 }[/math] אזי [math]\displaystyle{ a_n\lt b_n }[/math] החל משלב מסויים, ולכן אם [math]\displaystyle{ \sum_{k=1}^\infty b_k }[/math] מתכנס גם [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתכנס
- אחרת, [math]\displaystyle{ 0\lt c\in\mathbb{R} }[/math] והטורים חברים [math]\displaystyle{ \sum_{k=1}^\infty a_k ~ \sum_{k=1}^\infty b_k }[/math], כלומר [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתכנס אם ורק אם [math]\displaystyle{ \sum_{k=1}^\infty b_k }[/math] מתכנס

דוגמא:
- [math]\displaystyle{ \sum_{k=1}^\infty \frac{1}{\left(\sqrt[k]{k!}\right)^2} \sim \sum_{k=1}^\infty\frac{1}{k^2} }[/math]

מבחני השורש והמנה

יהי טור [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math]

מבחן המנה -
- אם [math]\displaystyle{ \overline{\lim}\left|\frac{a_{n+1}}{a_n}\right|\lt 1 }[/math] אזי הטור מתכנס בהחלט
- אם [math]\displaystyle{ \underline{\lim}\left|\frac{a_{n+1}}{a_n}\right|\gt 1 }[/math] אזי [math]\displaystyle{ a_n\not\to 0 }[/math] ולכן הטור מתבדר

מבחן השורש -
- אם [math]\displaystyle{ \overline{\lim}\sqrt[n]{|a_n|}\lt 1 }[/math] אזי הטור מתכנס בהחלט
- אם [math]\displaystyle{ \overline{\lim}\sqrt[n]{|a_n|}\gt 1 }[/math] אזי [math]\displaystyle{ a_n\not\to 0 }[/math] ולכן הטור מתבדר

שימו לב - במבחן השורש לוקחים את הגבול העליון בשני המקרים, ובמבחן המנה צריך שהעליון יהיה קטן מאחד, או התחתון גדול מאחד. זו לא טעות...

מבחן העיבוי

מבחן העיבוי-
- תהי [math]\displaystyle{ 0\leq a_n }[/math] סדרה מונוטונית יורדת אזי הטור [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] מתכנס אם ורק אם [math]\displaystyle{ \sum_{k=1}^\infty 2^k \cdot a_{(2^k)} }[/math] מתכנס

הוכחה:
- ראשית, נוכיח באינדוקציה כי [math]\displaystyle{ \sum_{k=1}^n 2^{k-1}a_{2^k} \leq \sum_{k=2}^{2^n} a_k }[/math] כלומר
- [math]\displaystyle{ a_2 + 2\cdot a_4 +4\cdot a_8+... = a_2 + a_4 + a_4 +a_8 + a_8 + a_8 + a_8 + ... \leq a_2 + a_3 + a_4 +a_5 + a_6 +a_7 +a _8 +... }[/math]
- כעת נוכיח באינדוקציה כי [math]\displaystyle{ \sum_{k=0}^{n-1} 2^k a_{2^k}\geq \sum_{k=1}^{2^n-1}a_k }[/math]
סה"כ אם הטור האחד מתכנס, הסס"ח של השני חסומה ולכן גם השני מתכנס.

הטור ההרמוני המוכלל

הטור [math]\displaystyle{ \sum_{n=1}^\infty \frac{1}{n^a} }[/math] מתכנס אם ורק אם [math]\displaystyle{ a\gt 1 }[/math]

דוגמאות:

[math]\displaystyle{ \sum_{k=1}^\infty\frac{1}{k\cdot\ln(k)} }[/math]

[math]\displaystyle{ \sum_{k=1}^\infty\frac{1}{\ln(k!)} }[/math]

עוד דוגמאות

מבחני התכנסות לטורים כלליים

מבחן דיריכלה

תהי סדרה [math]\displaystyle{ a_n\to 0 }[/math] סדרה מונוטונית יורדת לאפס
תהי סדרה [math]\displaystyle{ b_n }[/math] כך שההסס"ח שלה חסומה, כלומר קיים [math]\displaystyle{ M\gt 0 }[/math] כך שלכל n מתקיים [math]\displaystyle{ |S_n|=\left|\sum_{k=1}^nb_k\right|\lt M }[/math]
אזי הטור [math]\displaystyle{ \sum_{k=1}^\infty a_kb_k }[/math] מתכנס.

הוכחה:
נסמן ב[math]\displaystyle{ D_n }[/math] את סדרת הסכומים החלקיים של הטור [math]\displaystyle{ \sum_{k=1}^\infty a_kb_k }[/math] וב[math]\displaystyle{ S_n }[/math] את סדרת הסכומים החלקיים של [math]\displaystyle{ b_n }[/math].
יהיו [math]\displaystyle{ m\gt n\in\mathbb{N} }[/math]
- [math]\displaystyle{ D_m-D_n = \sum_{k=n+1}^m a_kb_k = \sum_{k=n+1}^m a_k(S_k -S_{k-1}) = \sum_{k=n+1}^m a_kS_k - \sum_{k=n}^{m-1} a_{k+1}S_k = a_mS_m -a_{n+1}S_n + \sum_{k=n+1}^{m-1} S_k(a_k-a_{k+1}) }[/math]
- [math]\displaystyle{ |D_m-D_n|\leq |a_m||S_m| + |a_{n+1}|S_n +\sum_{k=n+1}^{m-1} |S_k||a_k-a_{k+1}| }[/math]
- כעת נשתמש בעובדה כי [math]\displaystyle{ |S_n|\lt M }[/math] לכל n וכן [math]\displaystyle{ a_n - a_{n+1}\geq 0 }[/math] לכל n.
- [math]\displaystyle{ |D_m-D_n|\leq M\left(a_m + a_{n+1} +\sum_{k=n+1}^{m-1} a_k-a_{k+1}\right)= 2Ma_{n+1}\to 0 }[/math]
לכן [math]\displaystyle{ D_n }[/math] סדרת קושי ולכן מתכנסת לגבול סופי, כלומר הטור מתכנס.

מבחן לייבניץ

תהי [math]\displaystyle{ a_n\to 0 }[/math] סדרה מונוטונית יורדת לאפס. אזי:
- הטור [math]\displaystyle{ \sum_{k=1}^\infty (-1)^{k+1}a_k }[/math] מתכנס.
- [math]\displaystyle{ \left|\sum_{k=1}^\infty (-1)^{k+1}a_k\right|\leq a_1 }[/math].

הוכחה:
- כיוןן שהסס"ח של [math]\displaystyle{ (-1)^{n+1} }[/math] חסומה הטור מתכנס לפי מבחן דיריכלה.
- נסמן ב[math]\displaystyle{ S_n }[/math] את הסס"ח של הטור [math]\displaystyle{ \sum_{k=1}^\infty (-1)^{k+1}a_k }[/math].
- כיוון שהסדרה [math]\displaystyle{ a_n }[/math] יורדת, ניתן להוכיח באינדוקציה כי:
  - [math]\displaystyle{ S_{2n}\geq 0 }[/math]
  - [math]\displaystyle{ S_{2n-1}\leq a_1 }[/math]

סיכום בדיקת התכנסות 🖖

כיצד נבחן אם הטור [math]\displaystyle{ \sum a_n }[/math] מתכנס בהחלט, בתנאי או מתבדר?

אם ניתן להראות כי [math]\displaystyle{ a_n\not\to 0 }[/math] הטור מתבדר
נבצע מבחני ספוק 🖖
1. אם לפי מבחני ההשוואה (הראשון או הגבולי) הטור [math]\displaystyle{ \sum |a_n| }[/math] אינו מתכנס, אז אין התכנסות בהחלט, נעבר לבדוק התכנסות בתנאי.
2. אם במבחן המנה או השורש הגבול גדול מ1 הטור מתבדר, אם קטן מ1 הטור מתכנס בהחלט ואם שווה ל1 צריך לנסות משהו אחר.
3. אם במבחן העיבוי הטור [math]\displaystyle{ \sum |a_n| }[/math] אינו מתכנס, אז אין התכנסות בהחלט, נעבר לבדוק התכנסות בתנאי.
אם לא מצאנו התכנסות בהחלט, נבצע מבחנים על טורים כלליים בשביל לבדוק התכנסות בתנאי
1. מבחן לייבניץ
2. מבחן דיריכלה
3. עבודה ישירה על סדרת הסכומים החלקיים (טור טלסקופי למשל)

סכום האיברים החיוביים, וסכום האיברים השליליים

תהי סדרה [math]\displaystyle{ a_n }[/math] ונגדיר את:
- [math]\displaystyle{ a_n^+=\begin{cases}a_n & a_n\geq 0\\ 0 & a_n\lt 0\end{cases} }[/math]
- [math]\displaystyle{ a_n^-=\begin{cases}0 & a_n\geq 0\\ -a_n & a_n\lt 0\end{cases} }[/math]

[math]\displaystyle{ a_n=a_n^+-a_n^- }[/math]
[math]\displaystyle{ |a_n|=a_n^++a_n^- }[/math]

הטור [math]\displaystyle{ \sum a_k }[/math] מתכנס בהחלט אם ורק אם הטורים [math]\displaystyle{ \sum a_k^+, \sum a_k^- }[/math] מתכנסים שניהם.
אם הטור [math]\displaystyle{ \sum a_k }[/math] מתכנס בתנאי אזי הטורים [math]\displaystyle{ \sum a_k^+, \sum a_k^- }[/math] מתבדרים שניהם ושואפים לאינסוף.

כפי שהוכחנו בעבר בדרך שונה, אם הטור מתכנס בהחלט נובע ש[math]\displaystyle{ \sum a_k^+, \sum a_k^- }[/math] מתכנסים שניהם, וביחד עם העובדה ש[math]\displaystyle{ a_n=a_n^+-a_n^- }[/math] נובע שהטור מתכנס.

שינוי סדר הסכימה

תהי [math]\displaystyle{ f:\mathbb{N}\to\mathbb{N} }[/math] פונקציה הפיכה ותהי סדרה [math]\displaystyle{ a_n }[/math] אז נאמר ש[math]\displaystyle{ p_n=a_{f(n)} }[/math] היא שינוי סדר של הסדרה [math]\displaystyle{ a_n }[/math].

תרגיל - אם [math]\displaystyle{ a_n\to L }[/math] גם שינוי הסדר מקיים [math]\displaystyle{ b_n\to L }[/math]

דוגמא:
- [math]\displaystyle{ a_n=1,-1,1,-1,... }[/math]
- [math]\displaystyle{ f(n)=1,3,2,5,7,4,9,11,6,... }[/math]
- [math]\displaystyle{ p_n=a_{f(n)}=1,1,-1,1,1,-1,... }[/math]

בדוגמא האחרונה:
נסמן ב[math]\displaystyle{ S_n }[/math] את הסס"ח של [math]\displaystyle{ a_n }[/math] ומתקיים כי:
- [math]\displaystyle{ S_n=1,0,1,0,... }[/math]
נסמן ב[math]\displaystyle{ D_n }[/math] את הסס"ח של שינוי הסדר [math]\displaystyle{ p_n }[/math], מתקיים כי:
- [math]\displaystyle{ D_n =1,2,1,2,3,2,3,4,3,... }[/math]
שינוי הסדר אמנם הותיר את הטור מתבדר, אך הפך את סדרת הסכומים החלקיים מחסומה לשואפת לאינסוף.

משפט רימן

משפט רימן - יהי טור מתכנס בתנאי [math]\displaystyle{ \sum_{k=1}^\infty a_k }[/math] אזי לכל [math]\displaystyle{ -\infty\leq S \leq \infty }[/math] קיים שינוי סדר כך ש [math]\displaystyle{ \sum_{k=1}^\infty p_k=S }[/math]
כלומר, אם הטור מתכנס בתנאי, ניתן לגרום לו להתכנס לכל ערך שנרצה (ואף לשאוף לפלוס או מינוס אינסוף), על ידי שינוי סדר איברי הסדרה.

שינוי סדר הסכימה של טור מתכנס בהחלט

יהי טור מתכנס בהחלט [math]\displaystyle{ \sum_{k=1}^\infty a_k =S }[/math] אזי לכל שינוי סדר [math]\displaystyle{ p_n }[/math] מתקיים כי [math]\displaystyle{ \sum_{k=1}^\infty p_k=S }[/math]
כלומר, שינוי סדר איברי הסדרה אינו משפיע על סכום הטור.

פרק 4 - פונקציות ורציפות

מבוא לגבולות

מבוא לגבולות (שיטות אלגבריות: כפל בצמוד, הוצאת חזקה משמעותית).
- [math]\displaystyle{ \lim_{x\to 2}\frac{x^2-4}{x-2} }[/math]
- [math]\displaystyle{ \lim_{x\to\infty}\frac{2x^2+5x+3}{3x^2-100} }[/math]
- [math]\displaystyle{ \lim_{x\to \infty}\sqrt{x^2+1}-x }[/math]
- [math]\displaystyle{ \lim_{x\to \infty}\sqrt{x^2+x+1}-x }[/math]
- [math]\displaystyle{ \lim_{x\to\infty}x^2-x }[/math]

הגדרת הגבול לפי קושי

[math]\displaystyle{ \lim_{x\to x_0}f(x)=L }[/math] אם לכל סביבה של L בציר y קיימת סביבה של [math]\displaystyle{ x_0 }[/math] בציר x, כך שלכל ערכי x בסביבה של [math]\displaystyle{ x_0 }[/math] פרט אולי ל[math]\displaystyle{ x_0 }[/math] עצמו, ערכי ציר y כלומר [math]\displaystyle{ f(x) }[/math] נמצאים בסביבה של L בציר y.

דוגמאות:
- [math]\displaystyle{ \lim_{x\to 3} 2x+1=7 }[/math] אם לכל [math]\displaystyle{ \varepsilon\gt 0 }[/math] קיים [math]\displaystyle{ \delta\gt 0 }[/math] כך שלכל x המקיים [math]\displaystyle{ 0\neq |x-3|\lt \delta }[/math] מתקיים [math]\displaystyle{ |2x+1-7|\lt \varepsilon }[/math]
- [math]\displaystyle{ \lim_{x\to 2^-}\frac{1-x}{\sqrt{2-x}}=-\infty }[/math] אם לכל [math]\displaystyle{ M\gt 0 }[/math] קיים [math]\displaystyle{ \delta\gt 0 }[/math] כך שלכל x המקיים [math]\displaystyle{ 2-\delta\lt x\lt 2 }[/math] מתקיים כי [math]\displaystyle{ \frac{1-x}{\sqrt{2-x}}\lt -M }[/math]
- [math]\displaystyle{ y=a }[/math] אסימפטוטה אופקית מימין של [math]\displaystyle{ f(x) }[/math] אם לכל [math]\displaystyle{ \varepsilon\gt 0 }[/math] קיים [math]\displaystyle{ K\gt 0 }[/math] כך שלכל x המקיים [math]\displaystyle{ x\gt K }[/math] מתקיים כי [math]\displaystyle{ |f(x)-a|\lt \varepsilon }[/math]

הגדרת הגבול לפי היינה

[math]\displaystyle{ \lim_{x\to x_0}f(x)=L }[/math] אם לכל סדרת מספרים על ציר איקס [math]\displaystyle{ x_0\neq a_n\to x_0 }[/math] סדרת המספרים על ציר y מקיימת [math]\displaystyle{ f(a_n)\to L }[/math]
[math]\displaystyle{ \lim_{x\to x_0^+}f(x)=L }[/math] אם לכל סדרת מספרים על ציר איקס [math]\displaystyle{ x_0\lt a_n\to x_0 }[/math] סדרת המספרים על ציר y מקיימת [math]\displaystyle{ f(a_n)\to L }[/math]
[math]\displaystyle{ \lim_{x\to x_0^-}f(x)=L }[/math] אם לכל סדרת מספרים על ציר איקס [math]\displaystyle{ x_0\gt a_n\to x_0 }[/math] סדרת המספרים על ציר y מקיימת [math]\displaystyle{ f(a_n)\to L }[/math]

הגדרה זו שקולה להגדרה של קושי, כלומר הגבול שווה לL לפי קושי אם ורק אם הוא שווה לL לפי היינה.

מרבית כללי האריתמטיקה המורחבות נובעים "בחינם" עבור פונקציות

[math]\displaystyle{ \lim_{x\to x_0}f(x)=L }[/math] אם ורק אם [math]\displaystyle{ \lim_{x\to x_0^+}f(x)=\lim_{x\to x_0^-}f(x)=L }[/math]

הפונקציות הטריגונומטריות

הגדרת סינוס וקוסינוס ע"י מעגל היחידה.
- [math]\displaystyle{ sin^2(x)+cos^2(x)=1 }[/math]
- [math]\displaystyle{ sin(-x)=-sin(x),cos(-x)=cos(x) }[/math]
- [math]\displaystyle{ sin(a+b)=sin(a)cos(b)+sin(b)cos(a),cos(a+b)=cos(a)cos(b)-sin(a)sin(b) }[/math]
- [math]\displaystyle{ sin(2x)=2sin(x)cos(x),cos(2x)=cos^2(x)-sin^2(x) }[/math]

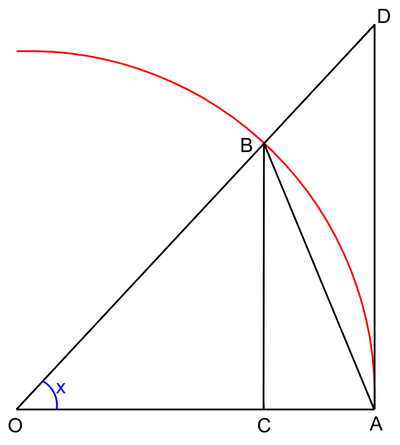
- עבור זוית [math]\displaystyle{ 0\lt x\lt \frac{\pi}{2} }[/math] שטח המשולש חסום בשטח הגזרה (משולש פיצה עם הקשה) שחסום בשטח המשולש:
- [math]\displaystyle{ S_{\triangle AOB}\lt S_{\bigcirc AOB}\lt S_{\triangle AOD} }[/math]
- [math]\displaystyle{ \frac{sin(x)}{2}\lt \frac{x}{2}\lt \frac{tan(x)}{2} }[/math]
  - כיוון ש[math]\displaystyle{ 0\lt sin(x)\lt x }[/math] בתחום [math]\displaystyle{ (0,\frac{\pi}{2}) }[/math], נובע לפי סנדוויץ' ש[math]\displaystyle{ \lim_{x\to 0^+}sin(x)=0 }[/math].
  - כיוון שמדובר בפונקציה אי זוגית, נובע שזה גם הגבול משני הצדדים.
  - כעת בתחום [math]\displaystyle{ (-\frac{\pi}{2},\frac{\pi}{2}) }[/math] הקוסינוס חיובית ולכן [math]\displaystyle{ cos(x)=\sqrt{1-sin^2(x)} }[/math] ונובע כי [math]\displaystyle{ \lim_{x\to 0}cos(x)=1 }[/math].
- נחלק את אי השיוויון הטריגונומטרי בסינוס ונקבל:
- [math]\displaystyle{ 1\lt \frac{x}{sin(x)}\lt \frac{1}{cos(x)} }[/math]
- לפי כלל הסנדביץ [math]\displaystyle{ \lim_{x\to 0^+}\frac{sin(x)}{x}=1 }[/math]
- כיוון שמדובר בפונקציה זוגית, נובע שהגבול משני הצדדים שווה 1.

ראינו ש[math]\displaystyle{ \lim_{x\to 0}\frac{sin(x)}{x}=1 }[/math].
שימו לב ש[math]\displaystyle{ \lim_{x\to\infty}\frac{sin(x)}{x}=0 }[/math], כיוון שמדובר בחסומה חלקי שואפת לאינסוף.

רציפות

רציפות.
הגדרה:
פונקציה f נקראית רציפה בקטע [math]\displaystyle{ [a,b] }[/math] אם f רציפה בכל נקודה בקטע [math]\displaystyle{ (a,b) }[/math] ובנוסף [math]\displaystyle{ \lim_{x\to a^+}f(x)=f(a) }[/math] וגם [math]\displaystyle{ \lim_{x\to b^-}f(x)=f(b) }[/math]

טענה: אם f רציפה ב[math]\displaystyle{ x_0 }[/math] אזי לכל סדרה [math]\displaystyle{ x_n\to x_0 }[/math] (גם אם אינה שונה מ[math]\displaystyle{ x_0 }[/math]) מתקיים כי [math]\displaystyle{ f(x_n)\to f(x_0) }[/math].

גבול של הרכבת פונקציות נכשל ללא רציפות.
- [math]\displaystyle{ f(x)=\frac{x}{x}, g(x)=0 }[/math] מתקיים כי [math]\displaystyle{ \lim_{x\to 0}f(x)=1,\lim_{x\to 2}g(x)=0 }[/math] אבל [math]\displaystyle{ \lim_{x\to 2}f(g(x))\neq 1 }[/math].

הרכבת רציפות: תהי f רציפה ב[math]\displaystyle{ x_0 }[/math] ותהי g רציפה ב[math]\displaystyle{ f(x_0) }[/math]. אזי [math]\displaystyle{ g\circ f }[/math] רציפה ב[math]\displaystyle{ x_0 }[/math].
- הוכחה:
- תהי סדרה [math]\displaystyle{ x_0\neq x_n\to x_0 }[/math] אזי [math]\displaystyle{ f(x_n)\to f(x_0) }[/math]
- לפי הטענה הקודמת, [math]\displaystyle{ g(f(x_n))\to g(f(x_0)) }[/math].

פונקציות הפיכות (הוכחות והגדרות מדוייקות בבדידה).
- פונקציה [math]\displaystyle{ f:[a,b]\to [c,d] }[/math] הפיכה אם"ם היא חח"ע ועל
- הפונקציה ההופכית היא [math]\displaystyle{ f^{-1}:[c,d]\to[a,b] }[/math] ומתקיים כי [math]\displaystyle{ f(x)=y }[/math] אם"ם [math]\displaystyle{ x=f^{-1}(y) }[/math]

טענה: אם [math]\displaystyle{ f:[a,b]\to [c,d] }[/math] רציפה בקטע [math]\displaystyle{ [a,b] }[/math], אזי [math]\displaystyle{ f^{-1}:[c,d]\to[a,b] }[/math] רציפה בקטע [math]\displaystyle{ [c,d] }[/math].
- הוכחה:
- תהי [math]\displaystyle{ y_0\neq y_n\to y_0 }[/math], צ"ל ש [math]\displaystyle{ f^{-1}(y_n)\to f^{-1}(y_0) }[/math]
- יהי גבול חלקי [math]\displaystyle{ x_n=f^{-1}(y_n)\to L }[/math].
- אזי [math]\displaystyle{ f(x_n)=y_n\to y_0 }[/math].
- מצד שני, לפי רציפות הפונקציה f מתקיים [math]\displaystyle{ f(x_n)\to f(L) }[/math].
- לכן [math]\displaystyle{ f(L)=y_0 }[/math] ולכן [math]\displaystyle{ L=f^{-1}(y_0) }[/math].

אי רציפות

מיון אי רציפות.
- רציפות - הגבול בנקודה שווה לערך בנקודה.
- סליקה - הגבול קיים וסופי בנקודה, אך שונה מהערך בנקודה או שהפונקציה אינה מוגדרת בנקודה.
- קפיצתית (מין ראשון) - הגבולות החד צדדיים קיימים סופיים ושונים בנקודה.
- עיקרית (מין שני) - אחד הגבולות החד צדדיים אינו קיים או שאינו סופי.

פרק 5 - גזירות

הגדרת הנגזרת

[math]\displaystyle{ f'(x)=\lim_{h\to 0}\frac{f(x+h)-f(x)}{h} }[/math]
[math]\displaystyle{ \displaystyle{\lim{h\to 0}} \frac{f(x_0+h)-f(x_0)}{h} =\{h=x-x_0\} = \lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0} }[/math]
- הסבר לגבי שיטת ההצבה בה השתמשנו לעיל:
- נניח כי [math]\displaystyle{ \lim{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}=f'(x_0) }[/math] ונוכיח כי [math]\displaystyle{ \lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=f'(x_0) }[/math], והוכחה דומה בכיוון ההפוך.
- תהי [math]\displaystyle{ x_0\neq x_n\to x_0 }[/math] נגדיר את הסדרה [math]\displaystyle{ 0\neq h_n=x_n-x_0\to 0 }[/math].
- כיוון ש[math]\displaystyle{ \frac{f(x_0+h_n)-f(x_0)}{h_n}\to f'(x_0) }[/math] נובע כי [math]\displaystyle{ \frac{f(x_n)-f(x_0)}{x_n-x_0}\to f'(x_0) }[/math].
אם f גזירה בנקודה, היא רציפה בנקודה:
- צ"ל [math]\displaystyle{ \lim_{x\to x_0}f(x)=f(x_0) }[/math]
- לפי אריתמטיקה של גבולות זה שקול ל [math]\displaystyle{ \lim_{x\to x_0}f(x)-f(x_0)=0 }[/math]
- לפי עקרון win (קיצור של wouldn't it be nice?) מתקיים כי [math]\displaystyle{ \lim_{x\to x_0}f(x)-f(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}\cdot (x-x_0)=f'(x_0)\cdot 0 = 0 }[/math]
פונקציה הערך המוחלט אינה גזירה באפס
- [math]\displaystyle{ (|x|)'(0) = \lim_{h\to 0}\frac{|h|-|0|}{h}=\lim\frac{|h|}{h} }[/math] וגבול זה אינו קיים, כיוון שהגבולות החד צדדים שונים.
- ניתן לשים לב גם ש[math]\displaystyle{ |x|=\sqrt{x^2} }[/math], וכמו כן נראה בהמשך כי[math]\displaystyle{ \sqrt{x} }[/math] אינה גזירה באפס.

הנגזרות של הפונקציות האלמנטריות

טריגו:
- [math]\displaystyle{ \lim_{h\to 0}\frac{1-cos(h)}{h}=\lim_{h\to 0}\frac{sin^2(h)}{h(1+cos(h))}=\lim_{h\to 0}sin(h)\cdot \frac{sin(h)}{h}\cdot \frac{1}{1+cos(h)}=0\cdot 1 \cdot \frac{1}{2}=0 }[/math]
- [math]\displaystyle{ (sin(x))'=\lim_{h\to 0}\frac{sin(x+h)-sin(x)}{h}=\lim_{h\to 0}\frac{sin(x)cos(h)+sin(h)cos(x)-sin(x)}{h}=\lim_{h\to 0}sin(x)\cdot \frac{cos(h)-1}{h} + cos(x)\cdot \frac{sin(h)}{h}=cos(x) }[/math]
- באופן דומה [math]\displaystyle{ (cos(x))'=-sin(x) }[/math]
לוג:
- [math]\displaystyle{ \lim_{h\to 0}\frac{log(1+h)}{h}=\lim_{h\to 0}\frac{1}{h}\cdot log(1+h)=\lim_{h\to 0}log\left(\left(1+h\right)^{\frac{1}{h}}\right)=log(e) }[/math]
  - המעבר האחרון נובע מהעובדה שפונקצית הלוג רציפה.
  - (בפרט נובע כי [math]\displaystyle{ \lim_{x\to 0}\frac{ln(1+x)}{x}=1 }[/math].)
- [math]\displaystyle{ (log(x))'=\lim_{h\to 0}\frac{log(x+h)-log(x)}{h}= \lim_{h\to 0}\frac{log\left(\frac{x+h}{x}\right)}{h}=\lim_{h\to 0}\frac{1}{x}\cdot\frac{log\left(1+\frac{h}{x}\right)}{\frac{h}{x}}=\frac{log(e)}{x} }[/math]
  - בפרט נובע כי [math]\displaystyle{ (ln(x))' = \frac{1}{x} }[/math]
אקספוננט:
- [math]\displaystyle{ \lim_{h\to 0}\frac{a^h-1}{h} = \{t=a^h-1, h=log_a(1+t)\} = \lim_{t\to 0} \frac{t}{log_a(1+t)} = \frac{1}{log_a(e)} = \frac{1}{\frac{ln(e)}{ln(a)}}=ln(a) }[/math]
- [math]\displaystyle{ (a^x)' = \lim_{h\to 0}\frac{a^{x+h}-a^x}{h}= \lim_{h\to 0}a^x\cdot \frac{a^h-1}{h}=a^x\cdot ln(a) }[/math]
  - בפרט נובע כי [math]\displaystyle{ (e^x)'=e^x }[/math].

ישר:
- [math]\displaystyle{ (x)'=\displaystyle{\lim_{h\to 0}\frac{(x+h)-x}{h} = 1} }[/math]

חוקי הגזירה

תהיינה f,g גזירות ב[math]\displaystyle{ x_0 }[/math] אזי:
- [math]\displaystyle{ (cf)'(x_0)=cf'(x_0) }[/math]
- [math]\displaystyle{ (f+g)'(x_0)=f'(x_0)+g'(x_0) }[/math]
- [math]\displaystyle{ (f\cdot g)'(x_0) = f'(x_0)\cdot g(x_0)+f(x_0)\cdot g'(x_0) }[/math]

תהי g גזירה ב[math]\displaystyle{ x_0 }[/math] ותהי f הגזירה ב[math]\displaystyle{ g(x_0) }[/math]:

[math]\displaystyle{ (f\circ g)'(x_0) = \lim_{x\to x_0} \frac{f(g(x))-f(g(x_0))}{x-x_0} }[/math]
תהי סדרה [math]\displaystyle{ x_0\neq x_n\to x_0 }[/math].
רוצים לומר ש[math]\displaystyle{ \frac{f(g(x_n))-f(g(x_0))}{x_n-x_0}= \frac{f(g(x_n))-f(g(x_0))}{g(x_n)-g(x_0)}\cdot \frac{g(x_n)-g(x_0)}{x_n-x_0}\to f'(g(x_0))\cdot g'(x_0) }[/math].
אמנם [math]\displaystyle{ g(x_n)\to g(x_0) }[/math] בגלל שהרציפות נובעת מהגזירות, אבל לא ידוע ש[math]\displaystyle{ g(x_n)\neq g(x_0) }[/math] ובמקרה זה אנחנו כופלים ומחלקים באפס.
אם יש תת סדרה [math]\displaystyle{ a_n }[/math] של [math]\displaystyle{ x_n }[/math] עבורה [math]\displaystyle{ g(a_n)=g(x_0) }[/math] אזי [math]\displaystyle{ \frac{g(a_n)-g(x_0)}{a_n-x_0}=0 }[/math] ולכן [math]\displaystyle{ g'(x_0)=0 }[/math].
לכן [math]\displaystyle{ f'(g(x_0))\cdot g'(x_0)=0 }[/math].
כמו כן, [math]\displaystyle{ \frac{f(g(a_n))-f(g(x_0))}{a_n-x_0}=0 }[/math].
לכן בכל מקרה קיבלנו כי [math]\displaystyle{ \frac{f(g(x_n))-f(g(x_0))}{x_n-x_0}\to f'(g(x_0))\cdot g'(x_0) }[/math]
סה"כ [math]\displaystyle{ (f\circ g)'(x_0)=f'(g(x_0))\cdot g'(x_0) }[/math].

נגזרת של חזקה

עבור [math]\displaystyle{ x\gt 0 }[/math] מתקיים [math]\displaystyle{ (x^\alpha)'=(e^{ln\left(x^\alpha\right)})' = (e^{\alpha\cdot ln(x)})' = e^{\alpha\cdot ln(x)}\cdot \frac{\alpha}{x} = x^\alpha \cdot \frac{\alpha}{x} = \alpha x^{\alpha-1} }[/math]

עבור חזקות בהן הביטוי מוגדר, [math]\displaystyle{ (x^\alpha)'=\alpha x^{\alpha-1} }[/math] גם עבור [math]\displaystyle{ x\leq 0 }[/math] (לפי תכונות של פונקציות זוגיות ואי זוגיות, ובאפס לפי חישוב ישיר).

חזקה:
- [math]\displaystyle{ (x^\alpha)'=\alpha x^{\alpha-1} }[/math] לכל [math]\displaystyle{ \alpha\in \mathbb{R} }[/math], הוכחה בהמשך.
בפרט:
- [math]\displaystyle{ (1)'=0 }[/math]
- [math]\displaystyle{ (\frac{1}{x})' = (x^{-1})'=-\frac{1}{x^2} }[/math]
- [math]\displaystyle{ (\sqrt{x})'=(x^{\frac{1}{2}})'=\frac{1}{2\sqrt{x}} }[/math]
- עבור [math]\displaystyle{ x\gt 0 }[/math] מתקיים [math]\displaystyle{ (\sqrt[3]{x})'=(x^{\frac{1}{3}})'=\frac{1}{3\sqrt[3]{x^2}} }[/math] וכיוון שהפונקציה אי זוגית נובע שהנגזרת שווה לביטוי הזה גם לשאר ערכי x.

דוגמא: חישוב הנגזרת של [math]\displaystyle{ x^x }[/math]

נגזרת מנה

תהיינה f,g גזירות בנקודה x כך ש [math]\displaystyle{ g(x)\neq 0 }[/math]:

נזכור כי [math]\displaystyle{ (\frac{1}{x})'=-\frac{1}{x^2} }[/math]
אזי בנקודה x מתקיים: [math]\displaystyle{ \left(\frac{f}{g}\right)'=\left(f\cdot \frac{1}{g}\right)' = f'\cdot \frac{1}{g} + f\cdot \frac{-g'}{g^2} = \frac{f'g-g'f}{g^2} }[/math]

פונקציות הופכיות ונגזרתן

טענה: תהי [math]\displaystyle{ f:[a,b]\to [c,d] }[/math] הפיכה ורציפה. ונניח כי היא גזירה בנק' [math]\displaystyle{ a\lt x_0\lt b }[/math] כך ש [math]\displaystyle{ f'(x_0)\neq 0 }[/math].

אזי [math]\displaystyle{ f^{-1} }[/math] גזירה בנק' [math]\displaystyle{ f(x_0) }[/math] ומתקיים כי

[math]\displaystyle{ (f^{-1})'(f(x_0))=\frac{1}{f'(x_0)} }[/math] או בנוסח אחר-

[math]\displaystyle{ (f^{-1})'(x)=\frac{1}{f'(f^{-1}(x))} }[/math]

- הוכחה:
- [math]\displaystyle{ (f^{-1})'(f(x_0)) = \lim_{y\to f(x_0)}\frac{f^{-1}(y)-f^{-1}(f(x_0))}{y-f(x_0)} }[/math]
- תהי [math]\displaystyle{ f(x_0)\neq y_n\to f(x_0) }[/math] ונסמן [math]\displaystyle{ x_n=f^{-1}(y_n) }[/math].
- אזי מתוך רציפות וחח"ע נובע כי [math]\displaystyle{ x_0\neq x_n\to f^{-1}(f(x_0))=x_0 }[/math]
- [math]\displaystyle{ \frac{f^{-1}(y_n)-f^{-1}(f(x_0))}{y_n-f(x_0)} = \frac{x_n-x_0}{f(x_n)-f(x_0)} \to \frac{1}{f'(x_0)} }[/math]

דוגמא חשובה:
[math]\displaystyle{ tan:(-\frac{\pi}{2},\frac{\pi}{2})\to\mathbb{R} }[/math] הפיכה וההופכית שלה נקראית [math]\displaystyle{ arctan }[/math].
[math]\displaystyle{ tan^2(x)+1 = \frac{sin^2(x)}{cos^2(x)}+1 = \frac{1}{cos^2(x)} }[/math]
[math]\displaystyle{ arctan'(x) = \frac{1}{\frac{1}{cos^2(arctan(x))}} = \frac{1}{tan^2(arctan(x))+1}=\frac{1}{1+x^2} }[/math]

הנגזרות של [math]\displaystyle{ arcsin,arccos }[/math]

פרק 6 - חקירה

משפט ערך הביניים

תהי f רציפה בקטע [math]\displaystyle{ [a,b] }[/math] כאשר [math]\displaystyle{ a\lt b\in\mathbb{R} }[/math].
עוד נניח כי [math]\displaystyle{ f(a)\leq 0 }[/math] וכן [math]\displaystyle{ f(b)\geq 0 }[/math].
אזי קיימת נקודה [math]\displaystyle{ c\in[a,b] }[/math] כך ש [math]\displaystyle{ f(c)=0 }[/math]

תהי f רציפה ב[math]\displaystyle{ [0,1] }[/math] כך ש[math]\displaystyle{ f(1)=2 }[/math], הוכיחו שקיימת נק' [math]\displaystyle{ c\in [0,1] }[/math] עבורה [math]\displaystyle{ f(c)=\frac{1}{c} }[/math]
- נעביר אגף ונביט בפונקציה [math]\displaystyle{ h(x)=f(x)-\frac{1}{x} }[/math] שצריך למצוא שורש שלה.
- [math]\displaystyle{ h(1)\gt 0 }[/math].
- [math]\displaystyle{ \lim_{x\to 0^+}h(x)=f(0)-\infty=-\infty }[/math] ולכן קיימת נקודה [math]\displaystyle{ 0\lt d\lt 1 }[/math] עבורה [math]\displaystyle{ h(d)\lt 0 }[/math].
- לפי משפט ערך הביניים בקטע [math]\displaystyle{ [d,1] }[/math] קיימת נק' המאפסת את הפונקציה h.

משפטי ויירשטראס

פונקציה רציפה בקטע סופי סגור - חסומה.
פונקציה רציפה בקטע סופי סגור - מקבלת מינימום ומקסימום.

משפט פרמה

אם פונקציה גזירה בנק' קיצון מקומי, הנגזרת שווה שם לאפס.
ההפך אינו נכון, ייתכן שהנגזרת תתאפס אך בנקודה לא יהיה קיצון ואף לא פיתול.

משפט רול

- תהי f רציפה ב[math]\displaystyle{ [a,b] }[/math] וגזירה ב[math]\displaystyle{ (a,b) }[/math] כך ש [math]\displaystyle{ f(a)=f(b) }[/math] אזי קיימת נקודה [math]\displaystyle{ c\in(a,b) }[/math] כך ש [math]\displaystyle{ f'(c)=0 }[/math]
כלומר, פונקציה רציפה בקטע סגור, וגזירה בקטע הפתוח, שמקבלת את אותו ערך בקצוות - הנגזרת שלה מתאפסת בנקודה כלשהי בקטע הפתוח.

לפולינום מדרגה n יש לכל היותר n שורשים שונים.

משפט לגראנז' ותחומי עלייה וירידה

פונקציה f נקראת עולה בתחום A אם לכל [math]\displaystyle{ x_1\lt x_2\in A }[/math] מתקיים כי [math]\displaystyle{ f(x_1)\leq f(x_2) }[/math]
פונקציה f נקראת יורדת בתחום A אם לכל [math]\displaystyle{ x_1\lt x_2\in A }[/math] מתקיים כי [math]\displaystyle{ f(x_1)\geq f(x_2) }[/math]

תהי f רציפה ב[math]\displaystyle{ [a,b] }[/math] וגזירה ב[math]\displaystyle{ (a,b) }[/math] אזי קיימת נקודה [math]\displaystyle{ c\in(a,b) }[/math] כך ש [math]\displaystyle{ f'(c)=\frac{f(b)-f(a)}{b-a} }[/math]
כלומר קיימת נקודה בה השיפוע שווה לשיפוע המיתר בין שתי הנקודות בקצוות הקטע.

תהי f רציפה ב[math]\displaystyle{ [a,b] }[/math] וגזירה ב[math]\displaystyle{ (a,b) }[/math] אזי f עולה בקטע [math]\displaystyle{ [a,b] }[/math] אם ורק אם [math]\displaystyle{ f'(x)\geq 0 }[/math] לכל [math]\displaystyle{ x\in[a,b] }[/math]
כמו כן, באותם תנאים, אם [math]\displaystyle{ f'(x)\geq 0 }[/math] לכל [math]\displaystyle{ x\in[a,b] }[/math] אזי [math]\displaystyle{ f(a)\lt f(b) }[/math] או שהפונקציה קבועה ב[math]\displaystyle{ [a,b] }[/math] ונגזרתה שווה אפס בקטע [math]\displaystyle{ (a,b) }[/math]

דוגמא
יהי [math]\displaystyle{ a\in\mathbb{R} }[/math] מצאו כמה פתרונות יש למשוואה [math]\displaystyle{ sin(x)=x+a }[/math]

משפט קושי (לגראנז' המוכלל)

תהיינה f,g רציפות ב[math]\displaystyle{ [a,b] }[/math] וגזירות ב[math]\displaystyle{ (a,b) }[/math] כך ש[math]\displaystyle{ g'\neq 0 }[/math] בקטע [math]\displaystyle{ (a,b) }[/math].
אזי קיימת נקודה [math]\displaystyle{ c\in(a,b) }[/math] כך ש [math]\displaystyle{ \frac{f'(c)}{g'(c)}=\frac{f(b)-f(a)}{g(b)-g(a)} }[/math]

הוכחת משפט לגראנז' המוכלל, שמוכיח גם את משפט לגראנז' עצמו כמקרה פרטי.
- ראשית, כיוון ש[math]\displaystyle{ g'(x)\neq 0 }[/math] בקטע [math]\displaystyle{ (a,b) }[/math] נובע לפי רול כי [math]\displaystyle{ g(a)\neq g(b) }[/math] ולכן מותר לחלק בהפרש ביניהם.
- [math]\displaystyle{ h(x)=f(x)-f(a) - \frac{f(b)-f(a)}{g(b)-g(a)}(g(x)-g(a)) }[/math]
- [math]\displaystyle{ h(a)=h(b)=0 }[/math] ולכן לפי רול קיימת נק' [math]\displaystyle{ c\in (a,b) }[/math] עבורה [math]\displaystyle{ h'(c)=0 }[/math] וזה מה שרצינו להוכיח.
- (שימו לב שמותר לחלק ב[math]\displaystyle{ g'(c) }[/math].)
- עבור [math]\displaystyle{ g(x)=x }[/math] נקבל את משפט לאגראנז' הרגיל.

כלל לופיטל

תהיינה פונקציות כך ש [math]\displaystyle{ f,g\to 0 }[/math] או [math]\displaystyle{ f,g\to \infty }[/math] ונניח כי [math]\displaystyle{ \frac{f'}{g'}\to L }[/math] אזי גם [math]\displaystyle{ \frac{f}{g}\to L }[/math]

משפט סדרי הגודל

לכל [math]\displaystyle{ 0\lt a,b }[/math] מתקיים כי:

[math]\displaystyle{ \displaystyle{\lim_{x\to\infty} \frac{x^a}{(e^x)^b} =0} }[/math]

[math]\displaystyle{ \displaystyle{\lim_{x\to\infty} \frac{x^a}{\ln^b(x)} =\infty} }[/math]

דוגמאות נוספות

[math]\displaystyle{ \displaystyle{\lim_{x\to 1} \frac{\ln(x)}{\sin(\pi x)} =-\frac{1}{\pi}} }[/math]

[math]\displaystyle{ \displaystyle{\lim_{x\to\infty} \frac{x}{sin(x)+2+x} =1} }[/math]

[math]\displaystyle{ \displaystyle{\lim_{x\to 0^+} xe^{\frac{1}{x}} =\infty} }[/math]

[math]\displaystyle{ \displaystyle{\lim_{x\to\infty} \sqrt[x]{x} =1} }[/math]

[math]\displaystyle{ \displaystyle{\lim_{x\to 0^+} x\ln(x) =0} }[/math]

[math]\displaystyle{ \displaystyle{\lim_{x\to 0^+} x^x =1} }[/math]

[math]\displaystyle{ \displaystyle{\lim_{x\to 0^+} \frac{1}{x}+\ln(x) =\infty} }[/math]

[math]\displaystyle{ \displaystyle{\lim_{x\to\frac{\pi}{2}} \left(\sin(x)\right)^{\tan^2(x)} =\frac{1}{\sqrt{e}}} }[/math]

[math]\displaystyle{ \displaystyle{\lim_{x\to(-\infty)} \frac{x}{\sqrt{x^2+1}} =-1} }[/math]

הוכחת כלל לופיטל בשני המקרים

אהבתם חדו"א 1? אז תעופו על חדו"א 2!

@@ שורה 43: / שורה 43: @@
 *[[מדיה:infi1moedA2021CS.pdf|מועד א' תשפ"א]], [[מדיה:infi1moedA2021CSSol.pdf|פתרון מועד א' תשפ"א]]
 *[[מדיה:infi1moedB2021CS.pdf|מועד ב' תשפ"א]], [[מדיה:infi1moedB2021CSSol.pdf|פתרון מועד ב' תשפ"א]]
-*[[מדיה:infi1moedC2021CS.pdf|מועד ג' תשפ"א]]
+*[[מדיה:infi1moedC2021CS.pdf|מועד ג' תשפ"א]], [[מדיה:infi1moedC2021CSSol.pdf|פתרון מועד ג' תשפ"א]]
 *[[מדיה:19CSInfi1dumbtest.pdf|מבחן לדוגמא תש"ף]]
 *[[מדיה:19CSInfi1A.pdf|מבחן מועד א' תש"ף]], [[מדיה:19CSInfi1ASol.pdf|פתרון מבחן מועד א' תש"ף]]